强化学习篇-由Policy-Gradient到Actor Critic-纯新手向

前言

最近家里发生点事情，刚刚也是跟老姐聊了很多散心回家。说到底我其实挺怕算法这些的，知道自己并不聪明，学起来挺费劲的，但也有不能放弃的理由。所以以博客的方式记录学习、记录一些idea，也是为了能够做到高效地理解这些知识，也免得没几天就给忘了要重新去捡起来学。最近精力大部分都花在准备课设上，所以暂时搁置了多级分类部署的部分（其实是还在加紧学Flask）。不过最近课设需要用到强化学习的东西，今天还是认真理解了Actor-Critic，在此推荐一下网上李宏毅老师的视频，讲得很清楚很明白。
根据我自己的经验，最好的学习方式就是通过自己的理解去教会别人，所以记录一下对我自己挺有帮助滴！

一、Basic Components

虽然今天我也是从零开始学习RL，不过这里我不打算过多赘述关于Actor/Environment/Reward Func三个比较基本的概念了。不过还是要稍微记录一下${\pi }_{\theta }$、episode、Trajectory以及Expected Reward的概念，毕竟这对于接下来推导Policy-Gradient以及Actor-Critic还是比较重要的。

${\pi }_{\theta }$-策略

在强化学习$\pi$中一般都用指代策略，而策略的作用是什么呢？一般比较直观来说，有这么一个表示：$a=\pi (s)$,即我们向策略输入一个状态（向量或矩阵），就期望能够通过策略返回一个action。不过一个好的策略$\pi$往往都是通过训练得到的，所以我们常看到$\pi (\theta )$，而这里的$\theta$其实只是说明这么一个策略函数$\pi$中含有待定参数$\theta$，而我们需要通过强化学习的方式去训练得到一个$\theta$，进而通过一个$\theta$对应一个策略函数$\pi$。

episode

如上图所示，episode就是指从某一个开始状态s1，经过一系列的action，辗转了一系列状态s2,s3,…,最终达到一个结束的状态，这样一个从开始探索到结束状态的过程就是一个episode。

Trajectory（轨迹）

视频中老师提到的Trajectory（轨迹），指的就是包含状态及动作action的一个序列，结合轨迹的含义还挺直观的嗷。这里要说明一下，$p_{\theta }(\tau )$指的呢就是在给定的$\theta$下一个episode中形成这么一个Trajectory轨迹的概率。对于trajectory中的每一个状态+动作，我们是以发生该状态的概率$p(s_n|s_{n-1},a_{n-1})$，乘上在该状态下通过策略选择到action $a_n$的概率$p(a_n|s_n)$。
最终呢形成上图中最下面的式子，其中其实可以分割为两部分来看待，$p_{\theta }(a_t|s_t)$实际上是通过我们训练的策略得到的，也即待会提到的actor，而$p(s_{t+1}|a_t)$则是通过环境反馈的。

E[R]-Expected Reward（Reward的期望值）

对于一个轨迹，我们可以将其某一个状态加动作(s+a)，视作处于某一个时间点，而我们可以通过环境的反馈得到一个对应该状态该动作的reward值，那么一个轨迹所对应的总Reward即应表示为$R(\tau )=\stackrel{T}{\underset{t=1}{\sum r_t}}$。
那么其实我们训练$\theta$的目的就是希望我们通过这个策略$\pi (\theta )$所形成的Trajectory轨迹对应的总Reward越大越好。由于肯定会产生多个轨迹，所以通过取轨迹Reward的期望值去衡量并且指导$\theta$的学习。

二、Policy-Gradient

Ok，讲完上面一些铺垫性的东西，来到Policy-Gradient。通过上面，我们知道训练的过程希望促使这个Expected Reward越大越好，所以会涉及到一个梯度的问题。这里直接引出一个梯度的推导过程：

看似很复杂，其实细看就没什么啦。图中框住的就是几个推导过程中运用的小技巧，感觉用语言描述起来还是太复杂了，但推导的这个过程还挺直观的就不多加赘述啦！而我们所要训练的$\theta$也是基于这个梯度，即$\theta \leftarrow \theta +\eta \nabla \overline{R_{\theta }}$($\eta$为学习率)。

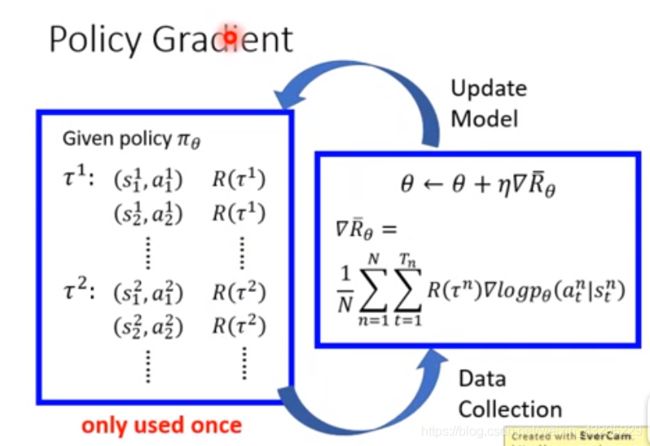
所以整个Policy-Gradient的流程就如上图所示，每一次我们都从环境去采样Sample一些诸如又边的数据，然后利用右边我们sample到的数据去支撑我们进行左边模型的update，进而模型的update即策略$\pi$的update再运用于实际环境和action再产生新的更为准确的数据。

baseline

接下来要提到的关键就是要添加一个Baseline。之所以要添加一个Baseline，是因为我们实际上很多情况下Reward值有可能一直都是正值，即体现在梯度中，$\nabla R_{\theta }$也会一直都为一个正值。这里会有点小绕（对我来说），我们训练一个$\theta$，是希望这个策略能够输出在当前state下，能够使得Expected Reward最大化的action。所以在梯度的引导下，我们训练输出的概率分布，明显提高那个能够最大化reward的action的占比。
而如果所有的action对应上述梯度都为正值，那么意思就是说在概率分布中，我们应该提高所有action的占比，这是不合理的，提高所有action的占比意味着某些原本较高占比的action反而占比会减少，就如上图中间所示。
为此，要设立一个baseline，即让Reward-baseline能取到正值也能取到负值，比较合理。一般而言就会取一个期望值作为baseline。

discount

这一步呢就是进一步的优化我们的Reward取值。上图的意欲还挺直观的，就是我们在考虑一个Trajectory的Reward的过程中，随着state的推进（t），我们只考虑state t及其之后到终结状态的reward值。有点像马尔可夫，就是不考虑当前状态之前那些reward了，认为过去发生的事情对当前乃至未来并不会有影响。同时在求取过程中乘上一个衰减因子$\gamma$，这个应该比较好理解，就比如乘一个0.9。意思就是认为距离当前状态越远的 对现在的影响应该越小，反之离当前状态越近的，对当前的状态影响越大。

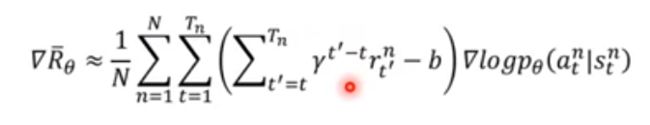
哇！终于把policy-gradient讲完了！！！那么上面结合到最后就是这么一个式子！接下来终于可以进入到Actor-Critic咯！

Actor-Critic-假

诶没进呢~
因为想到一个我认为可能像我一样纯新手会遇见的一个问题。就是

怎么做到梯度上升训练呢？

这一点是我觉得非常需要搞明白的。你看平时我们用到的大多数都是梯度下降算法，那么现在我们说希望做到梯度上升训练该怎么实现呢？我觉得有个关键点是需要先搞明白的！

最大似然估计与交叉熵

在我们刚才那串长长的看起来挺复杂的梯度推导式↑，我们可以发现唯一与$\theta$相关的项就是最后那个$p_{\theta }\left(a_t^n|s_t\right)$，这个呢，我的理解它是一个条件概率，一个似然（likelihood）。我们要使得每一次这个梯度Reward取得的值最大，就是要让这个似然取最大，即极大似然估计。
那么其实可以通过公式去证明，求极大似然估计基本等同于求最小交叉熵，这里由于篇幅问题就不过多赘述了。但要理解这一点，才能进一步明白为什么我们构建模型之后有的会选择使用交叉熵作为损失函数实现梯度上升。

三、Actor-Critic

呼！！！！！！终于真的来到Actor-Critic了，我真的要好好优化学习算法的门道了，虽然都用博客记录下来确实我自己很清楚整个算法的来龙去脉，但这也太耗时了！不过理解了上面的那些，接下来的Actor-Critic直接就可以轻松解决啦！

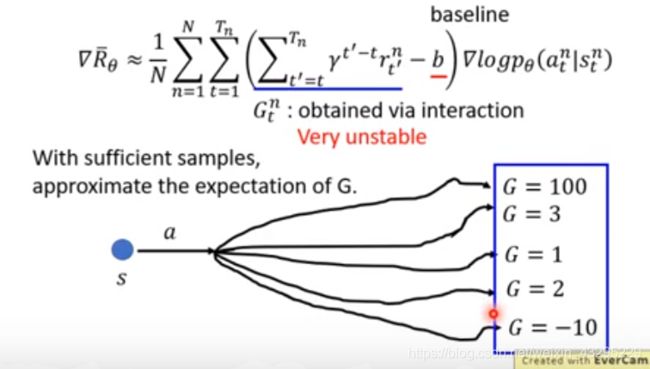
我喜欢学习他们这些算法推导的过程，总是对想出这些法子的大神们感到敬佩。我们可以看到如上图，如图所示G所指代的部分，其实随着我们sample到的数据变化，G也会变化。意思就是说，现在上式中G指代的部分，会随着我们sample的随机性，同样具备一定的随机性。所以同样，为了减少随机性带来的影响，我们取G的一个期望值E[G]。
那么这里就要提到两个来自Q-Learning的概念了，不过不打算过度深入的阐述：

简单来说，$V^{\pi }\left(s\right)$指的就是使用actor $\pi$(我们也可以认为是上面所说的策略),当我们观测到状态s时，它之后累计的reward值的一个期望值。
而$Q^{\pi }\left(s,a\right)$则指的时，使用actor $\pi$，以及当前状态为s，当选择采取action a，之后累计的reward值的一个期望值。那么说到这里，其实要知道上面的E[G]其实正是Q的定义呀！所以在Actor-Critic里面，我们直接用Q去替换之前的E[G]，再用V去替代b，得到如下：

所以本质上还是沿用了Policy-Gradient的路子。然后再这一步我们就会想，既然有Q又有V，莫非要用两个网络分别去训练这两个值？或者说有什么方法可以将这两者联系统一在一块？答案是有的，只要做出一点让步就行。

根据Q的定义我们得到的是上面的式子，但这里我们直接假设成下面的式子，这其中牺牲了一个求期望的过程，因此在这一块会出现一个方差。不过我们牺牲了这个换来的是什么呢，我们就可以用V去替换Q，得到：

我们这样就可以只训练一个用于求出V的网络啦（原先还得求Q呢）。当然这一部分的网络也就是Actor-Critic当中的Critic部分啦，就是用于输入状态向量S训练产生V值。
Actor网络的作用就是利用上述的梯度公式，用梯度上升的方式去训练，预测一个动作向量action，其中包括了各个动作的probability。
Critic预测的$V\left(s_n\right)$和$V\left(s_{n+1}\right)$会如上述公式所示最终作用于梯度公式，然后作用于Actor网络，进而影响action向量的产生。
整个拓扑结构基本如下：

四、代码实现

不上代码都是耍流氓哈！就以课程作业要用的Cartpole为例吧！

from keras.models import Sequential
from keras.optimizers import Adam
from keras.layers import Dense,Input
from keras.models import Model
import sys
import gym
import pylab
import numpy as np

class A2CAgent:
    def __init__(self, state_size, action_size,load_model=False):
        self.load_model = load_model
        self.state_size = state_size
        self.action_size = action_size
        self.value_size = 1

		#模型参数
        self.dense1_num=48;
        self.action_dense_num=32;
        self.critic_dense_num=16;
        self.discount_factor = 0.99#衰减因子
        self.actor_lr = 0.001#actor网络学习率
        self.critic_lr = 0.005#critic网络学习率
        self.actor,self.critic=self.build_model()

        if self.load_model:
            self.actor.load_weights("./model/actor.h5")
            self.critic.load_weights("./model/critic.h5")
	
	def build_model(self):#构建Actor-Critic模型如下
        input=Input(shape=(self.state_size,))
        dense1=Dense(self.dense1_num,activation='relu')(input)

        actor_dense=Dense(self.action_dense_num,activation='relu')(dense1)
        actor_output=Dense(self.action_size,activation='softmax')(actor_dense)
        actor=Model(input,actor_output)
        actor.compile(loss='categorical_crossentropy',optimizer=Adam(lr=self.actor_lr))#采用交叉熵，求最小交叉熵等于求极大似然

        critic_dense=Dense(self.critic_dense_num,activation='relu')(dense1)
        critic_output=Dense(self.value_size,activation='linear')(critic_dense)
        critic=Model(input,critic_output)
        critic.compile(loss='mse',optimizer=Adam(lr=self.critic_lr))

        return actor,critic
	    def get_action(self, state):#利用Actor部分进行网络的预测
        policy = self.actor.predict(state).flatten()
        return np.random.choice(self.action_size, 1, p=policy)[0]

    #训练模型
    def train_model(self, state, action, reward, next_state, done):
        target = np.zeros((1, self.value_size))
        advantages = np.zeros((1, self.action_size))#优势函数

        value = self.critic.predict(state)[0]#critic网络预测当前状态V值
        next_value = self.critic.predict(next_state)[0]#critic网络预测下个状态V值

        if done:
            advantages[0][action] = reward - value
            target[0][0] = reward
        else:
            #优势函数
            advantages[0][action] = reward + self.discount_factor * (next_value) - value#用于更新actor网络
            target[0][0] = reward + self.discount_factor * next_value#用于更新critic网络

        self.actor.fit(state, advantages, epochs=1, verbose=0)#不用展示详细训练过程
        self.critic.fit(state, target, epochs=1, verbose=0)
EPISODES = 1000

if __name__ == "__main__":
    env = gym.make('CartPole-v1')
    state_size = env.observation_space.shape[0]
    action_size = env.action_space.n
    agent = A2CAgent(state_size, action_size,load_model=False)
    scores, episodes = [], []

    for e in range(EPISODES):
        done = False
        score = 0
        state = env.reset()
        state = np.reshape(state, [1, state_size])

        while not done:
            env.render()
            action = agent.get_action(state)
            next_state, reward, done, info = env.step(action)
            next_state = np.reshape(next_state, [1, state_size])
            # 设定reward奖惩值
            reward = reward if not done or score == 499 else -100

            agent.train_model(state, action, reward, next_state, done)#每执行一次action训练一次

            score += reward
            state = next_state

            if done:
                score = score if score == 500.0 else score + 100
                scores.append(score)
                print("episode:", e, "  score:", score)

                # 如果连续十次记录score的平均值大于490，认为他已经训练好啦
                if np.mean(scores[-min(10, len(scores)):]) > 490:
                    sys.exit()

        # 保存模型
        if e % 50 == 0:
            agent.actor.save_weights("./model/actor.h5")
            agent.critic.save_weights("./model/critic.h5")

/