深度强化学习（8）Proximal Policy Optimization(PPO)

1. Trust region policy optimization(TRPO)

我们先来介绍TRPO。TRPO是英文单词Trust region policy optimization的简称，翻译成中文是置信域策略优化。
根据策略梯度方法，参数更新方程式为：

${\theta }_{new}={\theta }_{old}+\alpha {\nabla }_{\theta }J$

策略梯度算法的硬伤就在更新步长 $\alpha$ ，当步长不合适时，更新的参数所对应的策略是一个更不好的策略，当利用这个更不好的策略进行采样学习时，再次更新的参数会更差，因此很容易导致越学越差，最后崩溃。所以，合适的步长对于强化学习非常关键。

什么叫合适的步长？

所谓合适的步长是指当策略更新后，回报函数的值不能更差。如何选择这个步长？或者说，如何找到新的策略使得新的回报函数的值单调增，或单调不减。这是TRPO要解决的问题。
用 $\tau$ 表示一组状态-行为序列 $s_0,u_0,\cdots ,s_H,u_H$ ，强化学习的回报函数为：

$\eta \left(\tilde{\pi }\right)=E_{\tau |\tilde{\pi }}\left[{\sum }_{t=0}^{\infty }{\gamma }^t\left(r\left(s_t\right)\right)\right]$

这里，我们用 $\tilde{\pi }$ 表示策略。
刚才已经说过，TRPO是找到新的策略，使得回报函数单调不减，一个自然地想法是能不能将新的策略所对应的回报函数分解成旧的策略所对应的回报函数+其它项。只要新的策略所对应的其它项大于等于零，那么新的策略就能保证回报函数单调不减。其实是存在这样的等式，这个等式是2002年Sham Kakade提出来的。TRPO的起点便是这样一个等式：

$\eta \left(\tilde{\pi }\right)=\eta \left(\pi \right)+E_{s_0,a_0,\cdots \tilde{\pi }}\left[{\sum }_{t=0}^{\infty }{\gamma }^t{A}_{\pi }\left(s_t,a_t\right)\right]$ （1-1）

这里我们用 $\pi$ 表示旧的策略，用 $\tilde{\pi }$ 表示新的策略。其中，

$$\begin{gathered} A_{\pi }\left(s,a\right)=Q_{\pi }\left(s,a\right)-V_{\pi }\left(s\right) \\ =E_{s^{\prime }P\left(s^{\prime }|s,a\right)}\left[r\left(s\right)+\gamma V^{\pi }\left(s^{\prime }\right)-V^{\pi }\left(s\right)\right] \end{gathered}$$

称为优势函数。
（1-1）式可以展开为：

$\eta \left(\tilde{\pi }\right)=\eta \left(\pi \right)+{\sum }_{t=0}^{\infty }{\sum }_{s}P\left(s_t=s|\tilde{\pi }\right){\sum }_a\tilde{\pi }\left(a|s\right){\gamma }^t{A}_{\pi }\left(s,a\right)$

其中 $P\left(s_t=s|\tilde{\pi }\right)\tilde{\pi }\left(a|s\right)$ 为 (s,a) 的联合概率， ${\sum }_a\tilde{\pi }(a|s)$为求对动作 a 的边际分布，也就是说在状态s对整个动作空间求和；${\sum }_{s}P\left(s_t=s|\tilde{\pi }\right)$ 为求对状态 s 的边际分布，即对整个状态空间求和。
定义 ${\rho }_{\pi }\left(s\right)=P\left(s_0=s\right)+\gamma P\left(s_1=s\right)+{\gamma }^{2}P\left(s_2=s\right)+\cdots$
则：

$\eta \left(\tilde{\pi }\right)=\eta \left(\pi \right)+{\sum }_s{\rho }_{\tilde{\pi }}\left(s\right){\sum }_a\tilde{\pi }\left(a|s\right)A^{\pi }\left(s,a\right)$

如图所示：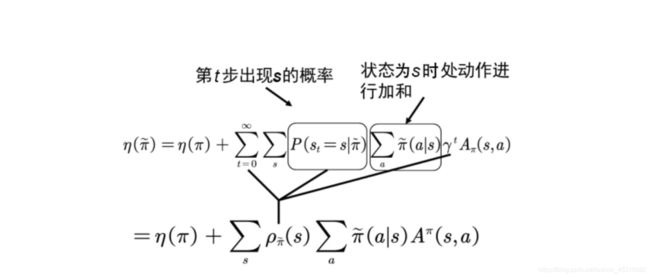
注意这里s是由新分布产生的，对新分布有很强的依赖性。这个公式其实在应用中完全无法达到，因为我们是为了得到新的策略，所以这里的其他项完全无从所知，为此，TRPO采取了一些技巧来解决这个问题。

TRPO第一个技巧

这时，我们引入TRPO的第一个技巧对状态分布进行处理。我们忽略状态分布的变化，依然采用旧的策略所对应的状态分布。这个技巧是对原代价函数的第一次近似。其实，当新旧参数很接近时，我们将用旧的状态分布代替新的状态分布也是合理的。这时，原来的代价函数变成了：

$L_{\pi }\left(\tilde{\pi }\right)=\eta \left(\pi \right)+{\sum }_s{\rho }_{\pi }\left(s\right){\sum }_a\tilde{\pi }\left(a|s\right)A^{\pi }\left(s,a\right)$

我们再看上式的第二项策略部分，这时的动作a是由新的策略 $\tilde{\pi }$ 产生。可是新的策略 $\tilde{\pi }$ 是带参数 $\theta$ 的，这个参数是未知的，因此无法用来产生动作。这时，我们引入TRPO的第二个技巧。

TRPO第二个技巧

TRPO的第二个技巧是利用重要性采样对动作分布进行的处理。

${\sum }_a{\tilde{\pi }}_{\theta }\left(a|s_n\right)A_{{\theta }_{old}}\left(s_n,a\right)=E_{aq}\left[\frac{{\tilde{\pi }}_{\theta }\left(a|s_n\right)}{q\left(a|s_n\right)}{A}_{{\theta }_{old}}\left(s_n,a\right)\right]$

通过利用两个技巧，我们再利用 $\frac{1}{1-\gamma }{E}_{s{\rho }_{{\theta }_{old}}}\left[\cdots \right]$ 代替 ${\sum }_s{\rho }_{{\theta }_{old}}\left(s\right)\left[\cdots \right]$ ；取 $q\left(a|s_n\right)={\pi }_{{\theta }_{old}}\left(a|s_n\right)$ ；

替代回报函数变为：

$L_{\pi }\left(\tilde{\pi }\right)=\eta \left(\pi \right)+E_{s{\rho }_{{\theta }_{old}},a{\pi }_{{\theta }_{old}}}\left[\frac{{\tilde{\pi }}_{\theta }\left(a|s\right)}{{\pi }_{{\theta }_{old}}\left(a|s\right)}{A}_{{\theta }_{old}}\left(s,a\right)\right]$

将 $L_{\pi }\left(\tilde{\pi }\right)\text{，}\eta \left(\tilde{\pi }\right)$ 都看成是策略 $\tilde{\pi }$ 的函数，则 $L_{\pi }\left(\tilde{\pi }\right)\text{，}\eta \left(\tilde{\pi }\right)$ 在策略 ${\pi }_{{\theta }_{old}}$ 处一阶近似。
在 ${\theta }_{old}$ 附近，能改善L的策略也能改善原回报函数。问题是步长多大呢？

再次引入第二个重量级的不等式:

$$\begin{gathered} \eta \left(\tilde{\pi }\right)⩾L_{\pi }\left(\tilde{\pi }\right)-C{D}_{KL}^{\max }\left(\pi ,\tilde{\pi }\right) \\ whereC=\frac{2\epsilon \gamma }{{\left(1-\gamma \right)}^2} \end{gathered}$$ （1-2）

其中 $D_{KL}\left(\pi ,\tilde{\pi }\right)$ 是两个分布的KL散度。我们在这里看一看，该不等式给了我们什么启示。

首先，该不等式给了 $\eta \left(\tilde{\pi }\right)$ 的下界，我们定义这个下界为
$M_i\left(\pi \right)=L_{{\pi }_i}\left(\pi \right)-C{D}_{KL}^{\max }\left({\pi }_i,\pi \right)$

下面利用这个下界，我们证明策略的单调性。
证明：
$\eta \left({\pi }_{i+1}\right)⩾M_i\left({\pi }_{i+1}\right)$且 $\eta \left({\pi }_i\right)=M_i\left({\pi }_i\right)$
则： $\eta \left({\pi }_{i+1}\right)-\eta \left({\pi }_i\right)⩾M_i\left({\pi }_{i+1}\right)-M\left({\pi }_i\right)$

如果新的策略 ${\pi }_{i+1}$ 能使得 $M_i$ 变大，那么有不等式 $M_i\left({\pi }_{i+1}\right)-M\left({\pi }_i\right)⩾0$ ，则 $\eta \left({\pi }_{i+1}\right)-\eta \left({\pi }_i\right)⩾0$，这个使得 $M_i$ 变大的新的策略就是我们一直在苦苦找的要更新的策略。那么这个策略如何得到呢？
（要找的更新策略其实就是使得不等式（1-2）下界最大的策略）
该问题可形式化为：

$maximiz{e}_{\theta }\left[L_{{\theta }_{old}}\left(\theta \right)-C{D}_{KL}^{\max }\left({\theta }_{old},\theta \right)\right]$

如果利用惩罚因子$C$则每次迭代步长很小，因此问题可转化为：

$$\begin{gathered} maximiz{e}_{\theta }{E}_{s{\rho }_{{\theta }_{old}},a{\pi }_{{\theta }_{old}}}\left[\frac{{\pi }_{\theta }\left(a|s\right)}{{\pi }_{{\theta }_{old}}\left(a|s\right)}{A}_{{\theta }_{old}}\left(s,a\right)\right] \\ subjectto \\ {D}_{KL}^{\max }\left({\theta }_{old},\theta \right)\le \delta \end{gathered}$$

需要注意的是，因为有无穷多的状态，因此约束条件 $D_{KL}^{\max }\left({\theta }_{old},\theta \right)$ 有无穷多个。问题不可解。

TRPO第三个技巧

在约束条件中，利用平均KL散度代替最大KL散度，即：

$subjectto{\bar{D}}_{KL}^{{\rho }_{{\theta }_{old}}}\left({\theta }_{old},\theta \right)\le \delta$

TRPO第四个技巧

$s\sim {\rho }_{{\theta }_{old}}\to s\sim {\pi }_{{\theta }_{old}}$

最终TRPO问题化简为：

$$\begin{gathered} maximiz{e}_{\theta }{E}_{s{\pi }_{{\theta }_{old}},a{\pi }_{{\theta }_{old}}}\left[\frac{{\pi }_{\theta }\left(a|s\right)}{{\pi }_{{\theta }_{old}}\left(a|s\right)}{A}_{{\theta }_{old}}\left(s,a\right)\right] \\ subjectto{E}_{s{\pi }_{{\theta }_{old}}}\left[D_{KL}\left({\pi }_{{\theta }_{old}}\left(\cdot |s\right)||{\pi }_{\theta }\left(\cdot |s\right)\right)\right]\le \delta \end{gathered}$$

2. PPO

PPO是基于Actor-Critic架构实现的一种策略算法， 属于TRPO的进阶版本。

PPO1
PPO1对应的 Policy 更新公式为：

$L^{KLPEN}(\theta )={\hat{\mathbb{E}}}_t\left[\frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{{\theta }_{\text{ old }}}\left(a_t|s_t\right)}{\hat{A}}_t-\beta \mathrm{K}\mathrm{L}\left[{\pi }_{{\theta }_{\text{ old }}}\left(\cdot |s_t\right),{\pi }_{\theta }\left(\cdot |s_t\right)\right]\right]$

在TRPO里，我们希望θ和θ’不能差太远，这并不是说参数的值不能差太多，而是说，输入同样的state，网络得到的动作的概率分布不能差太远。为了得到动作的概率分布的相似程度，可以用KL散度来计算。
PPO1算法的思想很简单，既然TRPO认为在惩罚的时候有一个超参数$\beta$难以确定，因而选择了限制而非惩罚。因此PPO1通过下面的规则来避免超参数的选择而自适应地决定$\beta$:

Compute $d={\hat{\mathbb{E}}}_t\left[\mathrm{K}\mathrm{L}\left[{\pi }_{{\theta }_{\mathrm{o}\mathrm{l}\mathrm{d}}}\left(\cdot |s_t\right),{\pi }_{\theta }\left(\cdot |s_t\right)\right]\right]$
If $d<d_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}}/1.5,\beta \leftarrow \beta /2$
If $d>d_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}}\times 1.5,\beta \leftarrow \beta \times 2$

PPO2
除此之外，原论文中还提出了另一种的方法来限制每次更新的步长，我们一般称之为PPO2，论文里说PPO2的效果要比PPO1要好，所以我们平时说PPO都是指的是PPO2，PPO2的思想也很简单，思想的起点来源于对表达式的观察。

首先做出如下定义：

$r_t(\theta )=\frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{{\theta }_{\text{ old }}}\left(a_t|s_t\right)},$ so $r\left({\theta }_{\text{ old }}\right)=1$

对应的 Policy 更新公式为：

$L^{CLIP}(\theta )={\hat{\mathbb{E}}}_t\left[\min \left(r_t(\theta ){\hat{A}}_t,\mathrm{clip}\left(r_t(\theta ),1-ϵ,1+ϵ\right){\hat{A}}_t\right)\right]$

在这种情况下可以保证两次更新之间的分布差距不大，防止了$\theta$更新太快。

PPO算法流程

参考文献：

[1] Trust Region Policy Optimization
[2] Proximal Policy Optimization Algorithms
[3] https://zhuanlan.zhihu.com/p/26308073
[4] https://www.jianshu.com/p/f4d383b0bd4c