数据结构笔记（4）——树（主要是关于二叉树）

这次讲讲树。

首先上定义：

树的定义

要注意的是：

1. 只有一个根结点（最顶上的那个结点）
2. 子树不相交

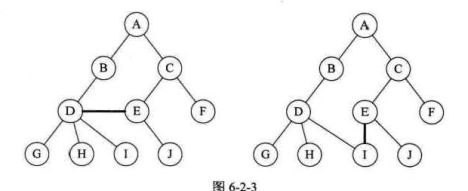
如上图所示，这就是子树相交的情况。

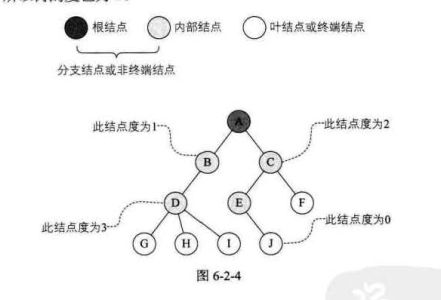
结点分类

结点之间关系

双亲是因为结点雌雄同体，同时是父亲也是母亲。

层

树的层（level）的概念是从根开始定义的，根是第一层，根的孩子为第二层，如此类推。

此外，如果将树中结点的子树看成从左至右有次序，不能互换，那么称为有序树，否则称为无序树。

---

二叉树

其实上面的大概知道就可以了，因为真正的重点是二叉树。

用图来表示就是：

总之，记住每个结点下的子结点最多只能够有两个就对了。

二叉树特点

1. 每个结点最多两颗子树
2. 左子树和右子树有顺序
3. 即使树中某结点只有一颗子树，也要区分左右

二叉树的五种形态

1. 空二叉树
2. 只有一个根结点
3. 根节点只有左子树
4. 根节点只有右子树
5. 根节点既有左子树又有右子树

上图为皇帝的空二叉树

只有一个根结点

根结点只有左子树

根结点既有左子树又有右子树

特殊二叉树

斜树

所有结点只有左子树就是左斜树， 反之是右斜树，两者统称斜树。

左斜树

右斜树

满二叉树

即一颗二叉树中，所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上。

完全二叉树

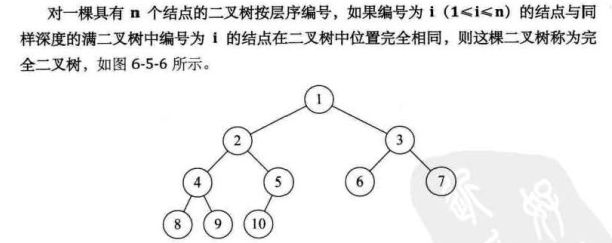
完全二叉树和满二叉树的不同在于，完全二叉树是满二叉树的子集，满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

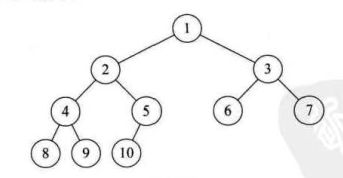
此外，完全二叉树的结点与同样深度的满二叉树，在按照层序编号的时候编号是一一对应的。例如：

对应的满二叉树：

由此可得出完全二叉树的一些特点：

1. 叶子结点只能出现在最下面的两层
2. 最下层的叶子一定集中在左部连续位置
3. 倒数二层如果有叶子结点一定都在右部连续位置
4. 如果结点度数为1，那么该节点只有左孩子，即不存在只有右子树的情况
5. 同样节点数的二叉树，完全二叉树的深度最小

所以判断一个二叉树是不是完全二叉树的方法就是：直接给每个结点按照层序进行编号，如果编号出现空当那么就说明不是完全二叉树。

二叉树性质

1. 在二叉树的第$i$层上最多有$2^{i-1}$个结点（$i\ge 1$）。
2. 深度为$k$的二叉树最多有$2^k-1$个结点。
3. 二叉树中，如果终端结点数为$n_0$，那么度为2的结点数为$n_2$，则$n_0=n_2+1$（终端节点数即叶子结点数）
4. 具有$n$个结点的完全二叉树深度为$\lfloor {\log }_{2}n\rfloor +1$（$\lfloor x\rfloor$是指对$x$向下取整）
5. 对一颗有$n$个结点的完全二叉树的结点按照层序编号，则对于每一个节点：

• 如果$i=1$那么结点$i$是二叉树的根，无双亲；如果$i>1$，那么其双亲是$\lfloor \frac{i}{2}\rfloor$；
• 如果$2i>n$，那么结点$i$无左孩子（即$i$是叶子结点），否则其左孩子是$2i$；
• 如果$2i+1>n$，那么$i$无右孩子，否则其右孩子是$2i+1$

性质1的证明（这里的性质都是用数学归纳法证明的）：

性质2：

性质3：

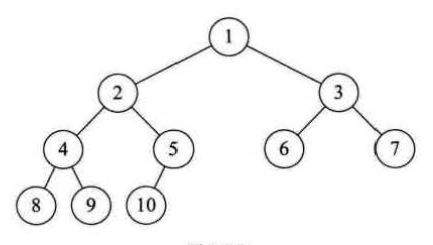
叶子结点：5（图中白色部分），度为2节点：4（图中深色部分）。

性质4：

可以直接通过性质2证明，这里就不多说了。

性质5：

二叉树的存储结构

分顺序存储结构和链式存储结构，顺序存储结构只能在二叉树是完全二叉树的情况下使用，不怎么用这种存储方式，所以这里就不说了。重点是二叉链表。

二叉链表

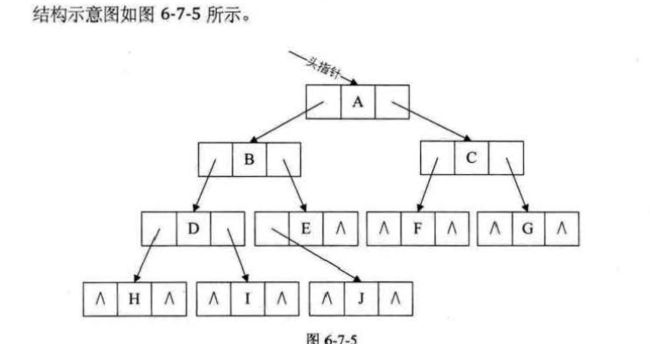
就是这玩意，data是数据域，lchild和rchild是指针域，分别指向左孩子和右孩子。

定义代码：

typedef struct BiTNode {
	TElemType data;
	struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

在这个结构的基础上建立的二叉树的结构如下图所示：

在这个基础上还有一些改进的版本，如为了更快速地进行遍历，添加了指向兄弟节点的指针域，这里就不提了。

二叉树的遍历

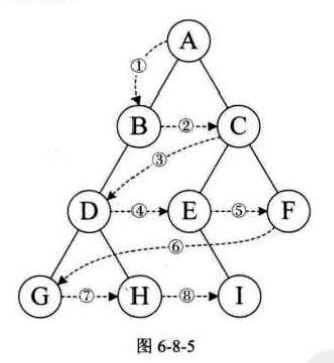
前序遍历

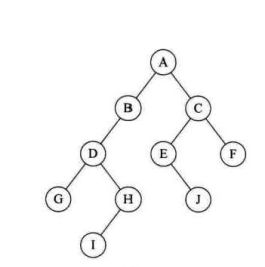
口诀：根左右。以此来分析下上图，首先从根开始，所以A，然后左，所以B，此时根设定为B，继续，左，D，左，G。G为根的时候发现没有左孩子和右孩子，所以返回D，最后，右，H。H没有孩子，所以返回D，D已经遍历过了，以此类推，返回到A，开始右，C。然后还是左，E，根结点为E时发现没有左孩子，所以遍历到I，最后I没有孩子，所以返回到E，E已经遍历过了，所以回到C，开始遍历右侧，所以F。所以最后的输出顺序是ABDGHCEIF。

中序遍历

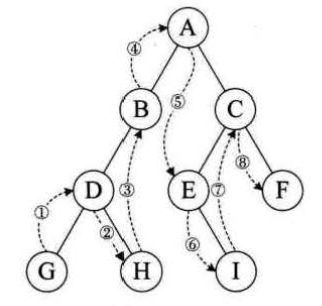
口诀：左根右（当成优先级来看待，优先遍历最左边的，其次根，最后右）

后序遍历

口诀：左右根

前中后序遍历的C++实现：

/* Given a binary tree, print its nodes according to the 
"bottom-up" postorder traversal. */
// 后序
void printPostorder(struct Node* node) 
{ 
    if (node == NULL) 
        return; 
  
    // first recur on left subtree 
    printPostorder(node->left); 
  
    // then recur on right subtree 
    printPostorder(node->right); 
  
    // now deal with the node 
    // 注意这行的位置，其实前中后序的实现组合是一样的，只是顺序不一样
    cout << node->data << " "; 
} 
  
/* Given a binary tree, print its nodes in inorder*/
// 中序
void printInorder(struct Node* node) 
{ 
    if (node == NULL) 
        return; 
  
    /* first recur on left child */
    printInorder(node->left); 
  
    /* then print the data of node */
    cout << node->data << " "; 
  
    /* now recur on right child */
    printInorder(node->right); 
} 
  
/* Given a binary tree, print its nodes in preorder*/
// 前序
void printPreorder(struct Node* node) 
{ 
    if (node == NULL) 
        return; 
  
    /* first print data of node */
    cout << node->data << " "; 
  
    /* then recur on left sutree */
    printPreorder(node->left);  
  
    /* now recur on right subtree */
    printPreorder(node->right); 
}  

层序遍历

即遍历完同一层再遍历下一层。

参考

《大话数据结构》：其实这本入门看看还行，深入的话还得看别的书……
Tree Traversals (Inorder, Preorder and Postorder)
关于前中后序排列