每日一题，每日一练。22编辑距离（被迫用动态规划时，没有一个子问题是无辜的）

72.编辑距离
给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = “horse”, word2 = “ros” 输出：3
解释： horse -> rorse (将 ‘h’ 替换为’r’) rorse -> rose (删除 ‘r’) rose -> ros (删除 ‘e’)

示例 2：

输入：word1 = “intention”, word2 = “execution” 输出：5
解释： intention ->inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

这是一道看上去非常难的题但是转述起来非常简单的题，我们现在把这道题转述一下，
给定两个字符串word1和word2，你可以往word1或word2中添加字符，或者修改word1的字符（这点也和修改word2的字符等价），求使得word1和word2相等的最小操作。
是的，由于这题并不需要最终字符串的最小长度，你可以将删除视为对另一个字符串的增加，于是这个问题变成了一个单向的问题，那么既然是单向，在相等的前一时刻我们是怎么操作的呢，我们有三种选择：
1：我们给word1加上一个字符，之后word1和word2就相等辣
2：我们给word2加上一个字符，之后。。。。。。。相等辣
3：我们换掉一个字符，之后。。。。。。。。辣

很显然，最终时刻相等的操作是每个时刻的相等的操作的集合，因此我们需要利用动态规划，于是我们先建立dp及边框（以1为例）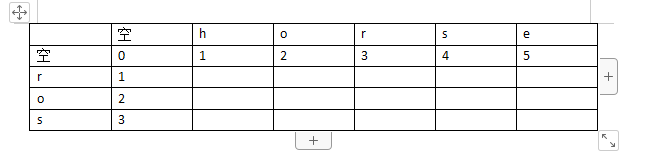
，
这里需要记住三点
1：每个位置的值是当前word1，word2需要达到相同经历的操作次数，也就是每个位置在经历这么多操作次数后已经达到了相等状态
2：在新的字符引入后，我们需要思考如何达到新的相等，比如如果word1多一个h，我们要么给对面加一个h，要么在对面的尾端（因为前面的字符串已经处理完成了）改一个h
3（重点）：我们需要知道是在什么基础状态下产生了新的待处理字符，这决定了我们之前是哪个状态的累计操作次数
边框的建立很简单因为最简单的是一个字符串为空的时候，我们只需要增加这个字符串就行了。做的操作次数就是字符串的长度，然后我们对每个部分进行来源查找，这里我们以word1=“h”，word2=“r”举例，也就是本表格中3行3列的位置，我们比较上一时刻的相等状态有三种办法，请记住我们只有增加和改动，删除已经等同于增加另一个。

1：可以看成由2行3列，也就是在h，空可以在一步操作到相等的状况下在word2又的尾端又需要多处理了一个r，变到了这里，那么相应的，我们需要给对面加一个r，多出一步操作
2：也有可能是3行2列，在空，r可以在一步操作到相等的状况下的时候，word1的尾端由需要多处理一个h，那么相应的，我们需要给对面加一个h，多出一步操作。
3：也有可能在2行2列，在空，空可以不进行操作相等的时候，两边同时多出一个字符分别为h和r，这个时候我们进行一步修改操作，让h变成r，用这一步来形成新的相等。

由于我们只进行一个字符的改动，因此只存在这三种情况（因为我们前文提到每一步的操作只有三种操作，也只有这三种可能通过一步操作达成新的相等）可以在一步改动中到达新的相等状态，这也是动态规划很重要的一点，就是逐步推进。即在之前已经确认状况的情况下，当前可能是一下三种状况之一。

我们需要再多处理一个word1字符
我们需要再多处理一个word2字符
我们需要再多处理一个word1字符和word2字符，用修改让他们相等

那么我们比较这三种方式那种更好，实际上的状态转移就是

dp[ii][i]=min(dp[ii-1][i]+1,dp[ii][i-1]+1,dp[ii-1][i-1]+1)

也就是在当前时刻，我们需要判断这个状态是比之前多处理word1的一个字符（多处理一行），还是比之前多处理word2的一个字符（多处理一列），还是word1和word2都比之前增加一个字符，而这个字符通过改变处理，这三种方式那个方式形成新的操作次数最少，注意这三种之前并不是一种状态，我们只用这三种是因为只有这三种形成的新状态符合动态规划，即一步操作可以形成新的相等

当然，有的人可能发现了问题，在增加操作不会有什么问题，因为如果我们视为这个状态是比之前增加一个字符，我们只要在另一个字符串也加一个字符就行了，这是固定的一步，但如果我们视为处理状况多两个字符，那么当出现表4行4列，word1=“ho”,而word2=“ro”时，如果我们把它视为第三种情况，即表3行3列word1=“h”而word2=‘r’时新增两个待处理字符通过修改解决的情况，我们会发现新增的字符并不需要修改，o和o是相等的，因此，我们需要对动态转移方程的第三步重新设定一个值check，如果新加入的两个字符是相等的，那么check=0，否则=1，新的DP方程构建如下

dp[ii][i]=min(dp[ii-1][i]+1,dp[ii][i-1]+1,dp[ii-1][i-1]+check)

我们再来回顾一下整道题的步骤

建立dp边界
从都有字符串的时候开始，推导之前的基础状况
更新当前状态的最小操作次数

代码如下：

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        dp=[[0 for i in range(len(word2)+1)]for i in range(len(word1)+1)]
        for i in range(len(dp[0])):#建立边界
            dp[0][i]=i
        for i in range(len(dp)):#建立边界
            dp[i][0]=i
        for ii in range(1,len(dp)):
            for i in range(1,len(dp[0])):
                if(word1[ii-1]!=word2[i-1]):
                    check=1
                else:
                    check=0
                dp[ii][i]=min(dp[ii-1][i]+1,dp[ii][i-1]+1,dp[ii-1][i-1]+check)#基于前三种状态看从哪边过来更好
        return dp[-1][-1]#回复给的这个状态需要多少次

逐步推进，稳扎稳打，学习也是大抵如此.