二叉树介绍,及简单二叉树存储(数组、链表),先序遍历序列创建二叉树,二叉树的三种简单遍历方式
一、树基本概念
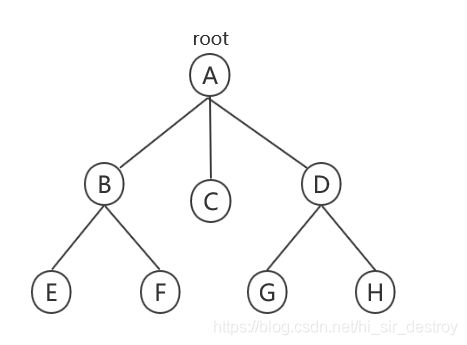
树:一种非线性的数据结构
结点:A、B、C等都是结点,结点不仅包含数据元素,而且包含指向子树的分支。
结点的度:结点拥有的子树个数或者分支个数。如A结点有3个子树,所以度为3
树的度:树中各结点度的最大值,如例子中结点最大的度为3(A的度),所以树的度为3,最小为0(叶子结点)
叶子结点:又叫终端结点,指度为0的结点,如E\F\G\H
孩子:结点的子树的跟,如A的孩子:BCD
双亲:子树的上层即双亲,如BCD双亲是A
祖先:从根到某节点路劲上的所有结点,如E的双亲是AB
层次:从根开始是第一层,根的孩子是第二层,....
树的高度:跟结点到某个叶子结点最长的路劲,如ABE ABF ADG ADH,都是3,所以树高为3
叶子结点:终端结点,如:EFGHC
二、二叉树
1.每个结点最多只有两个子树,即二叉树中的结点的度只能为0、1、2
2.二叉树有左右之分,不能颠倒
3.在一个二叉树中,如果所有的分支结点都有左孩子和右孩子结点,并且叶子结点都集中在二叉树的最后一层,则称为满二叉树
4.完全二叉树:要求最后一层叶子结点,均集中在左部连续位置,如存在结点为1的情况,则最后一个叶子结点只能是左子树。其余层结点如满二叉树。
5.二叉树结点总数 = 叶子结点个数 + 双分支结点个数 + 单分支结点个数 = 双分支结点个数 * 2 + 单分支个数结点 + 1 (+1是因为根节点前面没有分子)
6.二叉树分支总数 = 双分支结点个数 * 2 + 单分支个数结点 = 总结点数 - 1
7.非空二叉树上叶子结点个数 = 双分支结点数 + 1
8.二叉树的第i层最多有 2^(i-1)个结点(i>=1)
9.高度为K的二叉树。总结点数最多有 2^K-1个结点
10.给定n个结点,能构成C(n,2n)/(n+1)种不同的二叉树
11.具有n个结点的完全二叉树的高度(或深度)为log2(n) +1 向上取整,或为Log2(n+1)向下取整
12.二叉树存储结构(顺序存储结构):用一个数组来存,这种存储方式适合完全二叉树,存储一般二叉树会浪费较大空间。将完全二叉树种的结点值按编号依次存入一个一维数组中。
例,我们知道二叉树的某非叶子结点下标为i,且有孩子结点,则A的左孩子结点,只需访问Tree[2*i+1]即可,则A的右孩子结点,只需访问Tree[2*i+2]即可,
#include
#include
int tree[100];
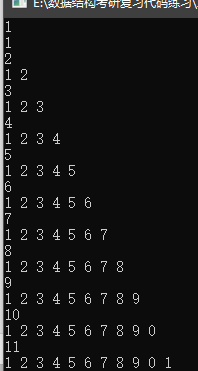
/* 二叉树 15个元素 假设二叉树的数据是1 2 3 4 5 6 7 8 9 0 1 …… 一直循环
1
2 3
4 5 6 7
8 9 0 1 2 3 4 5
*/
void print(int m)
{
for(int i=0;i 效果:每一行,一个数字的表示,待存储二叉树的个数,下面即存储的二叉树的数据。
13、链式存储结构。用链表实现,单个结点定义:
typedef struct node{
int data; //数据
struct node *lchild; //左孩子结点
struct node *rchild; //右孩子结点
}node; #include
#include
typedef struct node{
char data;
struct node *lchild;
struct node *rchild;
}node;
char chin[100];
int m;
/* 二叉树 15个元素 假设二叉树的数据是1 2 3 4 5 6 7 8 9 0 1 …… 一直循环
1
2 3
4 5 6 7
8 9 0 1 2 3 4 5
*/
//创建二叉树,按照上述数组形式创建的二叉树
void initChainTree(node *&q,int step) //从0开始。
{
if(step>=m||chin[step]=='0') //出口必须放在函数首部
{
return;
}
if(q==NULL)
{
q=(node *)malloc(sizeof(node));
q->lchild=NULL;
q->rchild=NULL;
}
q->data=chin[step];
printf("%c ",q->data);
initChainTree(q->lchild,step*2+1);
initChainTree(q->rchild,step*2+2);
}
void printChain(node *p)
{
while(p!=NULL)
{
printf("%d ",p->data);
//p->
}
}
int main() {
while(scanf("%s",chin)!=EOF)
{
//initArrayTree(m);
m=0;
while(chin[m]!='\0')
{
m+=1;
}
printf("%d ",m);
node *q;
q=NULL;
initChainTree(q,0) ;
}
} 以先序遍历序列的顺序创建二叉树
测试样例:ABC000DE0F00G00 (这是一个先序序列,0表示当前结点为空)
int initChain(node *&q,int step)
{
if(step>=m||chin[step]=='0')
{
return step;
}
if(q==NULL)
{
q=(node *)malloc(sizeof(node));
q->lchild=NULL;
q->rchild=NULL;
}
q->data=chin[step];
//printf("%c ",q->data);
step=initChain(q->lchild,++step);
step=initChain(q->rchild,++step);
}三、二叉树的三种遍历方式(如果二叉树为空树,就不访问结点信息)
1.先序遍历
1)访问根结点
2)先序遍历左子树
3)先序遍历右子树
void xianChine(node *q)
{
if(q!=NULL)
{
printf("%c ",q->data);
xianChine(q->lchild);
xianChine(q->rchild);
}
else
{
return;
}
} 2.中序遍历
1)先序遍历左子树
2)访问根结点
3)先序遍历右子树
void midChine(node *q)
{
if(q!=NULL)
{
midChine(q->lchild);
printf("%c ",q->data);
midChine(q->rchild);
}
else
{
return;
}
} 3.后序遍历
1)先序遍历左子树
2)先序遍历右子树
3)访问根结点
void lastChine(node *q)
{
if(q!=NULL)
{
lastChine(q->lchild);
lastChine(q->rchild);
printf("%c ",q->data);
}
else
{
return;
}
} 例子:
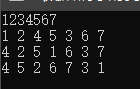
第一行 先构造数组、链表二叉树:1234567
第二行 先序遍历结果
第三行 中序遍历结果
第四行 后序遍历结果