leetcode42.接雨水/单调栈

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

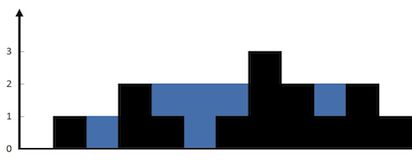
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/trapping-rain-water
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

基本思想

参考：leetcode
求这一列可以装多少水，按列求解。
求该列能够装多少水时，需要看该列两边的最大高度中较小的，分三种情况

• 较小的比该列还要小，那该列无法装水
• 较小的等于该列，该列也无法装水
• 较小的大于该列，该列可装的水等于较小的减去该列

class Solution {
public:
    int trap(vector<int>& height) {
        if(height.size()<3)
            return 0;
        int i,j,res=0;
        for(i=0;i<height.size();++i){
            //找该列左面的最大值
            int max_l=0;
            for(j=i-1;j>=0;--j){
                if(height[j]>height[max_l])
                    max_l=j;
            }
            
            //找该列右面的最大值
            int max_r=height.size()-1;
            for(j=i+1;j<height.size();++j){
                if(height[j]>height[max_r])
                    max_r=j;
            }
            
            j=(height[max_l]<height[max_r])?max_l:max_r;
            if(height[j]>height[i])
                res+=height[j]-height[i];
            
            //cout<<"i="<}
        return res;
    }
};

执行结果：通过
显示详情
执行用时 :536 ms, 在所有 C++ 提交中击败了5.08%的用户
内存消耗 :8.9 MB, 在所有 C++ 提交中击败了97.45%的用户

上述代码中其实存在着冗余，在寻找该元素的左面最大和右面最大的时候其实在每次寻找的时候会做很多重复的工作。
实际上如果左面的最大比该元素大，他依旧是左面的最大；如果右面的最大不是该元素，他依旧是右面的最大。

首先用两个数组，max_left [i] 代表第 i 列左边最高的墙的高度，max_right[i] 代表第 i 列右边最高的墙的高度。（一定要注意下，第 i 列左（右）边最高的墙，是不包括自身的，和 leetcode 上边的讲的有些不同）

对于 max_left我们其实可以这样求。

max_left [i] = Max(max_left [i-1],height[i-1])。它前边的墙的左边的最高高度和它前边的墙的高度选一个较大的，就是当前列左边最高的墙了。

对于 max_right我们可以这样求。

max_right[i] = Max(max_right[i+1],height[i+1]) 。它后边的墙的右边的最高高度和它后边的墙的高度选一个较大的，就是当前列右边最高的墙了。

class Solution {
public:
    int trap(vector& height) {
        //用时间换空间
        if(height.size()<3)
            return 0;
        vector max_l(height.size());//存放i左边的最大值
        vector max_r(height.size());//存放i右边的最大值
        //先求左面
        max_l[0]=0;
        for(int i=1;isize();++i){
            if(height[i-1]>max_l[i-1])
                max_l[i]=height[i-1];
            else
                max_l[i]=max_l[i-1];
        }
        //求右面
        max_r[height.size()-1]=0;
        for(int i=height.size()-2;i>=0;--i){
            if(height[i+1]>max_r[i+1])
                max_r[i]=height[i+1];
            else
                max_r[i]=max_r[i+1];
        }
        //求最终结果
        int res=0;
        for(int i=0;isize();++i){
            int cur=(max_l[i])?max_l[i]:max_r[i];
            if(cur>height[i])
                res+=(cur-height[i]);
        }
        return res;
    }
};

执行结果：通过
显示详情
执行用时 :4 ms, 在所有 C++ 提交中击败了95.83%的用户
内存消耗 :9 MB, 在所有 C++ 提交中击败了89.60%的用户

双指针法
参考：leetcode
其实上述思想可以继续优化，当前列的存水量是和左右两边的最大值中较小的有关系

• 初始情况，因为第0列和最后一列都无法装水，那再计算的时候左面left从第1列开始，右面从倒数第2列开始，那左面的最大值就是第0列的值，右面的最大值就是最后一列的值
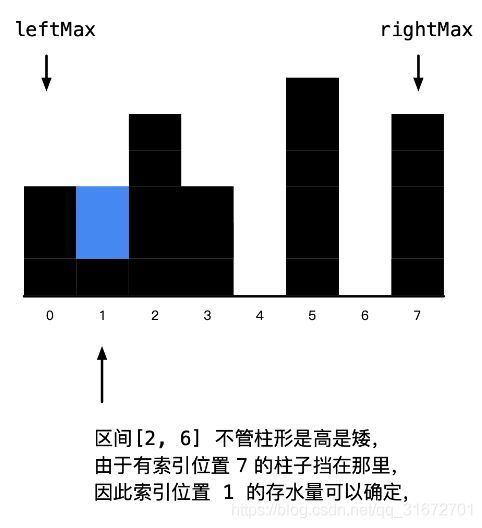
• 求解过程：每次都更新左面的最大值和右面的最大值相比较小的那一边，因为较小的那一边是决定因素（其左面或者右面的最大值），而另一边不一定是其真正的最大值，只是保证了他能装水的情况。就如下图所示：此时更新的是左面的情况，第1列左面的最大值是leftMax,其右面的最大值并不是rightMax,但rightMax保证了该列能装水，因为rightMax>leftMax
• 

class Solution {
public:
    int trap(vector& height) {
        //双指针法
        if(height.size()<3)
            return 0;
        int max_l=height[0];//左面的最大值
        int max_r=height[height.size()-1];//右面的最大值
        int left=1,right=height.size()-2;
        int res=0;
        while(left<=right){
            if(max_l{//左面的最大值小，靠近左面的装水                
                if(max_l>height[left])
                    res+=max_l-height[left];
                max_l=(max_l>height[left])?max_l:height[left];
                ++left;
            }
            else{//右面的最大值小，右面的装水               
                if(max_r>height[right])
                    res+=max_r-height[right];
                 max_r=(max_r>height[right])?max_r:height[right];
                --right;
            }
        }
        return res;
    }
};

栈
基本思想：

• 当前列的高度小于栈顶高度直接入栈
• 当前列的高度大于栈顶高度，栈顶出栈，计算当前元素和新的栈顶构成的区域的水，计算完后判断当前列和栈顶的高度，持续计算，直到走到最后一列

上述思想在计算的时候，当前列和新的栈顶相当于上述思想的右面的最大值和左面的最大值，计算的是出栈的这一列能盛多少水。
相当于横着计算水量。

class Solution {
public:
    int trap(vector<int>& height) {
        //用栈来实现
        stack<int> q;//栈存放的是下标
        if(height.size() < 3)
            return 0;
        q.push(0);
        int res = 0,i=1;
        while(i<height.size()){
            //当前列的值大于栈顶元素时，计算出栈列能盛多少水
            while(!q.empty()&&height[i]>height[q.top()]){
                int t=q.top();//当前出栈的列
                q.pop();
                
                //计算出栈列的水量,当前列和栈顶列之间的水量
                if(!q.empty()){
                    int min=(height[i]<height[q.top()])?height[i]:height[q.top()];
                    res+=(i-q.top()-1)*(min-height[t]);
                }                
            }
            q.push(i);
            ++i;
        }
        return res;
    }
};

执行结果：通过
显示详情
执行用时 :4 ms, 在所有 C++ 提交中击败了95.83%的用户
内存消耗 :9.7 MB, 在所有 C++ 提交中击败了69.64%的用户

单调栈

class Solution {
public:
    int trap(vector<int>& height) {
        if(height.size() < 3)
            return 0;
        stack<int> st;
        
        int res = 0;
        for(int i = 0; i < height.size(); ++i){
            if(st.empty() || height[i] < height[st.top()])
                st.push(i);
            else{
                while(!st.empty() && height[i] > height[st.top()]){
                    int h = height[st.top()];
                    st.pop();
                    if(st.empty())
                        break;
                    int w = i - st.top() - 1;
                    res += w * (min(height[i], height[st.top()]) - h);
                    
                }
                st.push(i);
            }
        }
        return res;
    }
};
/*
一层一层的计算雨水
遍历数组，寻找比当前元素大的两边的最近的元素，计算此围城的雨水
维护一个单调递减栈，当出现单调增的元素时，说明此元素可作为墙
*/