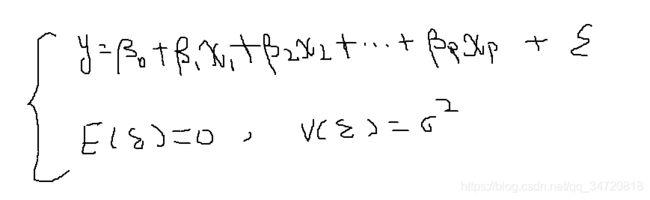从统计学中学习机器学习的基本知识梳理

从统计学中学习机器学习的基本知识梳理

前言：

本文从统计学入手，梳理统计学中机器学习的基本知识，从概念和思想上理解统计学的基础以及监督学习，非监督学习，半监督学习和强化学习。

一、统计学框架

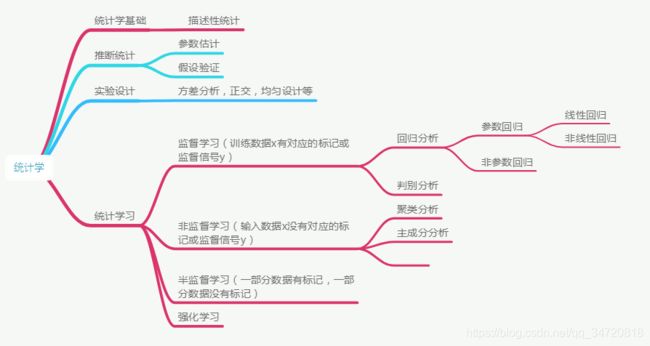
统计学：研究随机现象和统计规律性的一门学科。研究如何以有效的方式收集、整理和分析受随机因素影响的数据。它以概率论为基础推断或预测受随机因素影响的数据。本文讲解统计学内容如下：

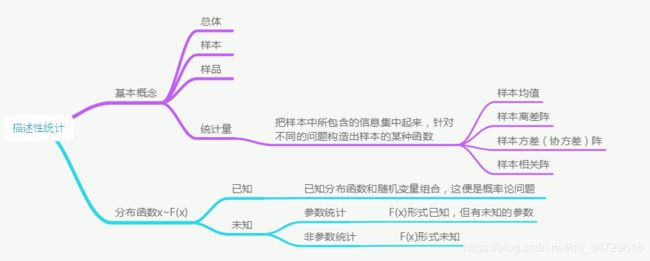
二、描述性统计

1、总体、个体、样品、样本、样本容量之间的关系

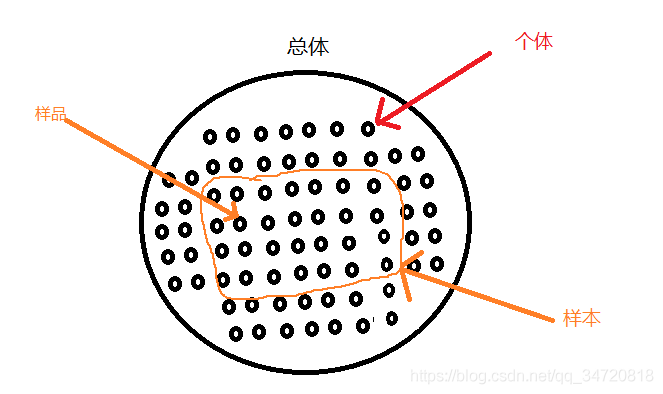
个体组成总体，总体抽取若干个体形成样本，样本由样品组成，因此样品一定是个体，而个体不一定是样品，样本的数量称为样本容量。他们之间关系的示意图如下：

2、样本表示为x₍₁₎ ，x₍₂₎ ，… ，x_(n) ，其中x_(i)=(x_i1，x_i2，…，x_ip)^T

3、样本矩阵表示为

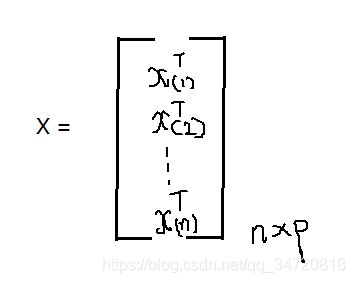
4、设x₍₁₎ ，x₍₂₎ ，… ，x_(n)是总体X的样本，T（x₍₁₎ ，x₍₂₎ ，… ，x_(n)）是样本的实值函数，且不包含任何位置参数，则成T（x₍₁₎ ，x₍₂₎ ，… ，x_(n)）为统计量。对于单总体常见的统计量有：

5、对于多总体情况：k个总体 G₁，G₂，…，G_k
对于每个总体G_α(α=1,2,…,k),都有相应的样本矩阵X_α=(x_ij^(α))，维数：n_α*p
把k个样本矩阵拼在一起（上下叠在一起）构成一个总的样本矩阵

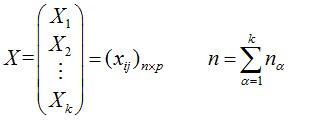
三、监督学习

1、对于样本数据x有对应标记y的监督学习，根据研究对象y为定性或者定量数据的情况，分别进行判别或者回归分析。
2、定性数据是连续量，取值无限且数据有大小；定性数据是离散量，取值很少（一般2-10个），通常数据无大小。其实定性和定量并没有一个明确的界限。
3、回归分析是研究自变量和因变量之间的关系，回归模型如下：

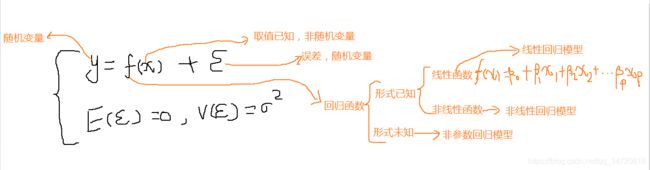
4、经验回归方程用于对模型进行估计，方程如下：

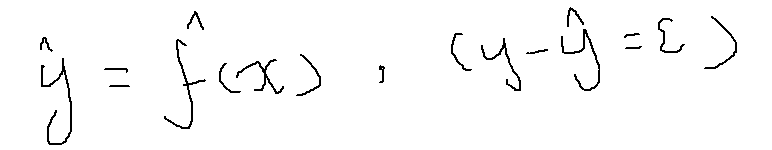
四、线性回归

1、线性回归模型如下
2、线性回归工作流程：

1、参数估计，解出β₀，β₁，β₂，…，β_p
2、假设检验回归函数是否为线性（通过F统计量检验）
3、得到经验回归方程y尖，进行估计
4、变量选择
5、模型评价

3、回归模型误差平方和Q公式如下：

4、最小二乘估计

1、使得误差平方和Q达到最小值的方法就是最小二乘估计，推导得最小二乘估计公式如下

2、最小二乘估计的优点是公式简单显示，直接套公式就可以得到结果且是无偏估计；缺点是公式中一旦|Z^TZ|=0，则无法得到结果。

3、|Z^TZ|=0的常见情况有两种，一种是样本数量n<

5、最小一乘估计和岭估计
1、误差绝对值之和公式如下：

2、使得误差绝对值之和达到最小的方法称为最小一乘估计

3、岭估计是对最小二乘估计缺点的优化，其减少了|Z^TZ|=0的情况，公式如下：

6、线性回归模型效果评价（检验）
1、对于回归模型效果的评价，差用误差平方和的方法进行评价。若训练出的回归模型在样本数据中计算的误差平方和越小，则表明该模型越好。

2、但仅仅使用训练样本计算误差平方和去评价模型的好坏很明显有所有不足，因为训练样本计算的误差平方和值仅仅表明回带效果或拟合效果，而不能表明预测效果的好坏。因此需要将样本数据在使用前划分为两个样本，一个用于训练模型和检验拟合效果，这个样本称为训练样本；另一个用于检验预测效果，这个样本称为测试样本。

3、那么如何在训练模型之前将样本数据划分为训练样本和测试样本两个部分呢？
如果样本数据充足，那么一般按照8：2的比例将样本数据分别划分为训练样本和测试样本；
如果样本数据太少，那么可以使用K折法，或者留一法（K折法中的k取1）进行样本数据的划分。
总之，模型更注重的是预测效果的好坏，在保证拟合效果和预测效果的同时，需要更加注重预测效果，可以参照此原则进行样本数据的划分。

7、线性回归模型函数中变量的选择
1、如果模型中变量过多会导致计算复杂、预测y值很复杂（就像医生检查病一样，如果指标太多了，那么检查的程序就很复杂）并且很可能导致高维数据（正常线性回归模型要求n>5p，即样本数量是变量的5倍）

2、传统的变量选择有
向前法：一个一个的加入变量，同时一个一个的计算误差平方和进行评价，最终得到合适数量的变量。
向后法：先得到一个考虑所有变量的复杂模型，再一个一个的删除变量，同时一个一个的计算误差平方和进行评价，最终得到合适数量的变量。
逐步法：是为了解决向前或向后存在的增加或者删除变量后就无法再将其删除或者增加进模型中的问题。逐步法及考虑在模型中加入变量又考虑删除变量
全部法：衡量和评价所有变量组合模型的好坏（全局最优），但一般计算量太大，目前几乎不能在现实中运用。

3、采用参数估计与变量选择同时进行的方法
比如LASSO方法，在参数估计的同时，结果得到的解中很多变量的参数为0（稀疏解），其中参数为0的变量就可以舍去，这就起到了变量选择的作用。

五、非参数回归

1、对于一个回归模型，如果并不知道回归函数的形式，那么这种情况下，我们及不必考虑回归函数形式，而是直奔主题，直接估计待估计y_n+1的值。

2、非参数回归的思想是： 通过确定样本数据中每个标记y_i对于所需求的y_n+1所造成的影响大小即权重w_i，进而将各个y_i与权重w_i相乘并求和得到的结果就是y_n+1的估计值。

举个例子：比如有一个样本数据是某班级所有女同学的体重和身高数据，那么某一天一个漂亮的妹子转入本班，妹纸知道自己的体重但并不知道自己的身高，那么如何得知她的身高是多少呢？这种情况我就可以采取权重求和来解决，首先将班级中体重与她相近的女同学的身高赋予较大的权重，相差较大的赋予较小的权重，之后进行加权求和求平均，就可以得到这个妹子的大概身高。这种思路就是非参数回归思想。

3、非参数回归模型的经验回归方程如下

4、那么有两个问题
第一、如何选择权重函数呢？
基本原则是x_i与x_n+1关系越接近，那么权重值越大

第二、用什么衡量x_i与x_n+1的关系呢？
大部分用x_i与x_n+1之间的距离来衡量，距离越小，则相关越大。因此可以理解核函数中k(u)中的(x_i – x)是x与x_i之间的距离。

5、基于第一个问题的原则，那么核函数k(u)应满足以下条件：

6、常用的核函数有高斯核和均匀核

7、因此非参数回归必须要确定三件事
首先，确定核函数k(u)
其次，确定窗宽h_n
最后，确定如何计算x_i与x之间的距离

根据研究结果表明，核函数的选择不是很重要，关键是窗宽的选择对结果影响很大。所以，我们大可不必纠结用什么核函数（大多是用高斯核），而应该把重心放在如何确定自己的窗宽

六、判别分析

1、距离判别

距离判别的思想就是样品x距离哪个总体G_α最近，那么就把这个样品判别为总体G_α。即对于任一样品x，若D（x，G_i）=minD（x，G_α）其中，1=<α<=k，则判定x属于G_i

根据上面距离判别思想的解释，我们可以知道距离判别关键在于距离的求解，那么距离是什么呢？又如何求距离呢？

1.1、首先，只要满足三个公理就是距离
第一、非负性 D(x,y)>=0
第二、对称性 D(x,y)=D(y,x)
第三、满足三角不等式 D(x,y)<=D(x,z)+D(z,y)
满足这三个条件的情况很多，因此距离也有很多，常见的距离有：

1.2、每个样品都是一个p维向量，我们可以把样品看作p维空间上的一个点。具体距离包括如下：

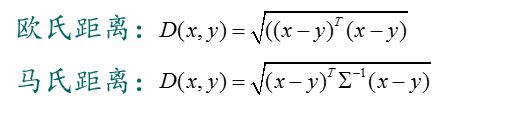
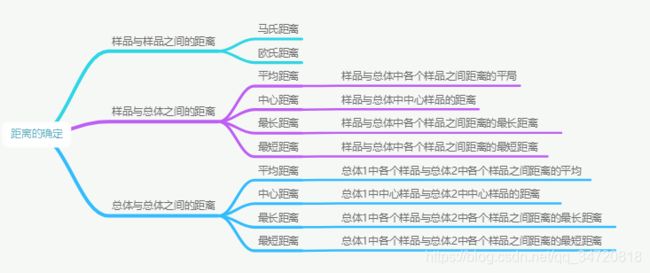
1.3、具体距离计算公式如下：
样品与样品之间的距离，设样品x₁，x₂来自总体G={x₁，x₂，…，x_n}

样品与总体之间的距离，设样品为x，总体为G={x₁，x₂，…，x_n}，总体的均值为  μ，方差为∑。

总体与总体之间的距离，总体1为G₁={x₁，x₂，…，x_n}，总体1的均值μ₁，方差为∑₁；总体2为G₂={y₁，y₂，…，y_m}，总体1的均值为μ₂，方差为∑₂。

1.4、判别方法评价
使用正确率来评价判别方法的好坏，正确率是经判别方法，正确样本个数m与总样品个数n之比，即m/n；

回代正确率：用训练样本计算的正确率，表明回代效果（拟合效果）
预测正确率：用测试样本计算的正确率，表明预测效果

1.5、距离判别优缺点
优点：简单直观
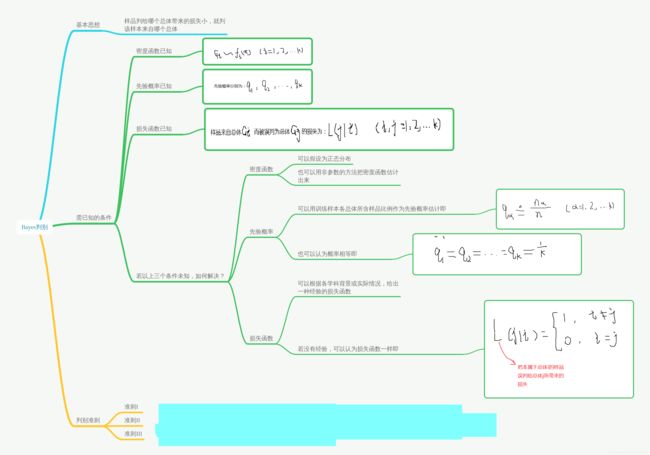
缺点：不知如何确定距离（距离类型很多）；把总体等同看待，没有考虑到总体会以不同的概率出现，认为判别方法与总体各自出现的概率大小无关，判别方法与判错之后所造成的损失无关，没有考虑误判之后所造成的损失差异。

2、Bayes判别

1、Bayes判别准则I

对任一样品x，计算样品判给G_α所造成的损失D_α(x)，判给哪个总体的损失越小，就把该样品判给哪个总体，即若D_t(x)=min D_α(x) （1=<α<=k），则判定x属于G_t，D_α(x)计算公式如下：

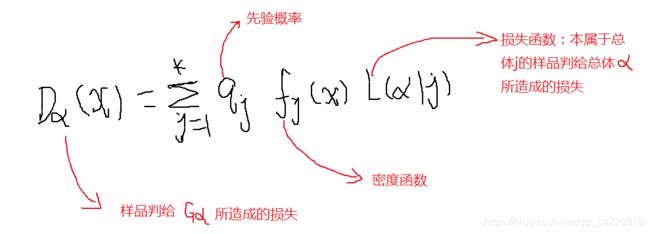
2、Bayes判别准则II

如果损失函数L(j|i)在i不等于j时都相同，则采用概率最大原则，即对任一样品x，若q_tf_t(x) = max q_αf_α(x) 其中1=<α<=k，则判定x属于G_t，这种判别方法不要将损失函数计算其中了。

3、Bayes判别准则III
待更新…

3、Fisher判别

待更新…

4、支持向量机

待更新…

5、随机深林

5.1、集成学习思想
5.2、自助法
5.3、bagging
5.4、决策树

待更新…

七、非监督学习

1、主成分分析

1.1、理论思想、算法和相关注意






1.2、简单例子
某中学生身体四项指标数据

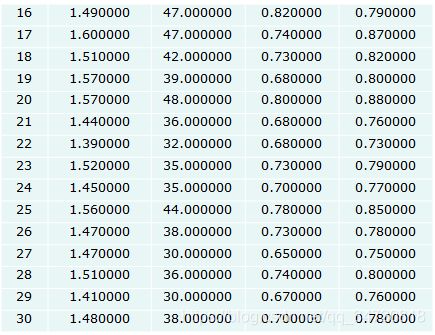
2、聚类分析

1、聚类分析整体框架图

2、系统聚类法（谱系聚类法）知识结构图

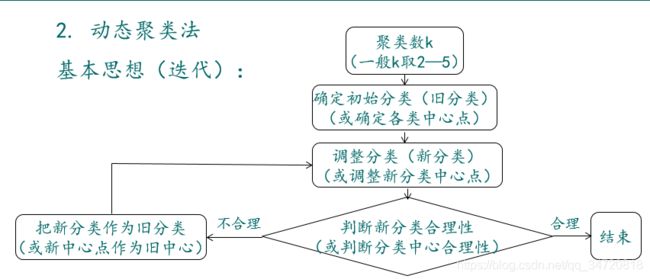
2.1、基本算法：
基本算法：用k表示剩下的总类数，用i表示聚类的次数。
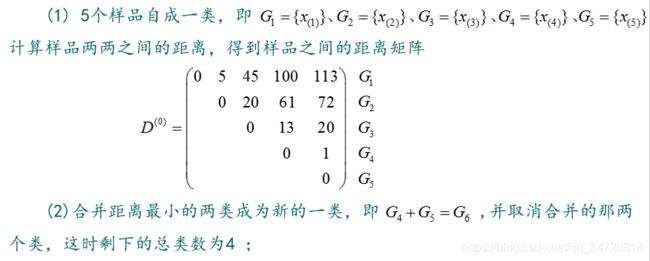
(1)每个样品自成一类，计算样品两两之间的距离，得到样品之间的距离矩阵 D⁽⁰⁾ =(d⁽⁰⁾_ij)_n*n ，这时i=1,k=n；
(2)合并距离最小的两类成为新的一类，并取消合并的那两个类，这时剩下的总类数k=n-i；
(3)计算距离矩阵D⁽ⁱ⁾ =(d⁽ⁱ⁾_ij)_k*k：对矩阵 D^(i-1) ，删除合并的那两个类所在的行和列，再增加一行一列，即新类与剩余的其它类之间的距离，就得到D⁽ⁱ⁾；
(4) i=i+1;
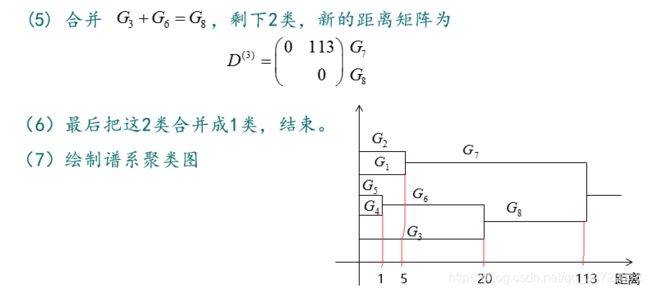
(5) 重复步骤(2)～(4)，直到 k=1 ；
(6) 绘制聚类图。
2.2 、简单例子

3、动态聚类（k-means）知识结构图

3.1、k-means（关注中心点）的简单例子