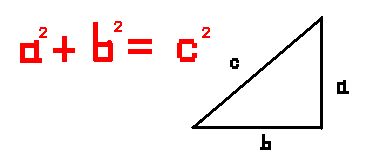最短路(Floyed-Warshall、Dijkstra、Bellman-Ford、SPFA)

Description

平面上有n个点(N<=100)，每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。若有连线，则表示可从一个点到达另一个点，即两点间有通路，通路的距离为两点直线的距离。现在的任务是找出从一点到另一点之间的最短路径。

Input

输入文件short.in共有n+m+3行，其中：
第一行为一个整数n。
第2行到第n+1行（共n行），每行的两个整数x和y，描述一个点的坐标(以一个空格隔开)。
第n+2行为一个整数m，表示图中的连线个数。
此后的m行，每行描述一条连线，由两个整数I,j组成，表示第i个点和第j个点之间有连线。
最后一行：两个整数s和t，分别表示源点和目标点。

Output

输出文件short.out仅一行，一个实数(保留两位小数)，表示从S到T的最短路径的长度。

---

4种做法

知道俩点的坐标之后，就可以用勾股定理求出它们之间的距离了。

勾股定理

---

1. Floyed-Warshall算法O(N^3)
2. Dijkstra算法O(N^2)
3. Bellman-Ford算法O(NE)
4. SPFA算法O(kE)

---

1.Floyed-Warshall算法O(N^3)

Floyed-Warshall可以算出任何俩个点之间的最优解，而且不排除有负值的情况。
具体算法大概是
枚举一个点k，接着枚举，i，j。
然后看看借k从i到j比直接从i到j是否更近一点。
（看上去十分简单暴力）

Floyed-Warshall代码

#include
#include
#include
using namespace std;
int t=0,n,m,x[101],y[101];
double D[101][101];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
	  scanf("%d%d",&x[i],&y[i]);
	scanf("%d",&m);
	int xx,yy;
	memset(D,0x7f,sizeof(D));
	for(int i=1;i<=m;++i){
		scanf("%d%d",&xx,&yy);
		D[xx][yy]=D[yy][xx]=sqrt(pow(double(x[xx]-x[yy]),2)+pow(double(y[xx]-y[yy]),2));
	}
	int q,z;
	scanf("%d%d",&q,&z);
	for(int k=1;k<=n;++k)
	  for(int i=1;i<=n;++i)
	    for(int j=1;j<=n;++j)
	      if(i!=j&&i!=k&&k!=j&&D[i][j]>D[i][k]+D[k][j])
	        D[i][j]=D[i][k]+D[k][j];
	printf("%0.2f",D[q][z]);
}

---

2.Dijkstra算法O(N^2)

Dijkstra无法处理带有负权值的图。
它从一个点开始，寻找到最近的一个点，判断、改变那个点连接的其他点 到原点的距离。然后再找另外的一个最近的点，重复操作。

Dijkstra代码

#include
#include
#include
using namespace std;
int t=0,n,m,x[101],y[101];
double D[101][101],c[101];
bool B[101];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
	  scanf("%d%d",&x[i],&y[i]);
	scanf("%d",&m);
	int xx,yy;
	for(int i=1;i<=n;++i)
	  for(int j=1;j<=n;++j)
	    D[i][j]=1e30;
	for(int i=1;i<=m;++i){
		scanf("%d%d",&xx,&yy);
		D[xx][yy]=D[yy][xx]=sqrt((x[xx]-x[yy])*(x[xx]-x[yy])+(y[xx]-y[yy])*(y[xx]-y[yy]));
	}
	int q,z;
	scanf("%d%d",&q,&z);
	for(int i=1;i<=n;++i)
	  c[i]=D[q][i];
	B[q]=1;
	c[q]=0;
	for(int i=1;i<n;++i){ 
		double minn=1e30;
		int k=0;
		for(int j=1;j<=n;++j) 
           if((!B[j])&&c[j]<minn){
                minn=c[j];
                k=j;
            }
        if(k==0) break;
        B[k]=1;
        for(int j=1;j<=n;j++)
           if(c[j]>c[k]+D[k][j]&&!B[j]) 
             c[j]=c[k]+D[k][j];
	}
	printf("%0.2lf\n",c[z]);
}

---

3.Bellman-Ford算法O(NE)

Bellman-Ford无法处理带负权回路的情况。
所以它是可以判断一个图是否有环的！（？？
原理大概是枚举所有的边，然后更新边连接的俩个点的距离。如果n轮过后，所有的点都没有更新，即现在就是最优解了。

Bellman-Ford代码

#include
#include
#include
#include
using namespace std;
int n,x[101],y[101],m,A[10001],B[10001],q,z;
double K[101],Z[10001];
bool L;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
		scanf("%d%d",&x[i],&y[i]);
	scanf("%d",&m);
	for(int i=1;i<=m;++i){
		scanf("%d%d",&A[i],&B[i]);
		Z[i]=sqrt(double((x[A[i]]-x[B[i]])*(x[A[i]]-x[B[i]]))
		+double((y[A[i]]-y[B[i]])*(y[A[i]]-y[B[i]])));
	}
	scanf("%d%d",&q,&z);
	memset(K,0x7f,sizeof(K));
	K[q]=0;
	for(int i=1;i<n;++i){  //这个算法顶多计算n-1轮，不然就是图上存在环

		L=false;
		for(int j=1;j<=m;++j){  //枚举边
			if(K[A[j]]+Z[j]<K[B[j]])  //是否能更新
			{
				K[B[j]]=K[A[j]]+Z[j];
				L=1;
			}
			if(K[B[j]]+Z[j]<K[A[j]])
			{
				K[A[j]]=K[B[j]]+Z[j];
				L=1;
			}
		
		}
		if(!L) break;  //没有更新过
	}
	printf("%.2lf",K[z]);
	return 0;
}

---

4.SPFA算法O(kE)

关于SPFA，（他死了），用于求一个点到其他点的最优距离
对比Bellman-Ford算法，SPFA少了更多的沉余操作。我们发现，Bellman-Ford 中，有很多边进行了没用的计算，所以SPFA算法就只算了新更新的点所连接的边。
（所以，邻接表派上用场了！！！）
这个算法莫明像Bellman-Ford与Dijkstra的结合体？？？

#include
#include
#include
#include
using namespace std;
int n,m,L[101],x[101],y[101],t=0;
double C[101],J[101][101];
bool B[101];
struct KKK{
	int y,next;
} a[10001];
void SPFA(int k){
	queue<int> Q;
	Q.push(k);
	memset(C,0x7f,sizeof(C));
	C[k]=0;
	while(Q.size()){  //还有更新过的点
		int l=Q.front();  //取出队头
		Q.pop();  //弹出
		B[l]=false;
		for(int i=L[l];i;i=a[i].next)  //枚举连接的点
		  if(C[a[i].y]>C[l]+J[a[i].y][l]){  //如果可以更新距离
		  	C[a[i].y]=C[l]+J[a[i].y][l];
		  	if(!B[a[i].y])  //压入队列
		  		Q.push(a[i].y);
		  }
	}
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
	  scanf("%d%d",&x[i],&y[i]);
	scanf("%d",&m);
	int l1,l2;
	for(int i=1;i<=m;++i){
		scanf("%d%d",&l1,&l2);
		J[l1][l2]=J[l2][l1]=sqrt((x[l1]-x[l2])*(x[l1]-x[l2])+(y[l1]-y[l2])*(y[l1]-y[l2]));  
		//计算直线距离
		a[++t].y=l2;a[t].next=L[l1];L[l1]=t;  //邻接表储存
		a[++t].y=l1;a[t].next=L[l2];L[l2]=t;
	}
	scanf("%d%d",&l1,&l2);
	SPFA(l1);
	printf("%.2f",C[l2]);
}