最短路入门合辑(附模板代码及水题)
最短路
大致题意:求一个点到另一个点的最短距离
解法:Floyd、Dijkstra、Bellman-ford、Spfa
关键名词:
1、源:
可以理解为图的起点,很好理解,就像是一条流水线的源头。
2、有向和无向
有向就是这个图的方向是固定的,只能从这边到那边,那边过不来,无向就是方向不固定。
3、权值、负权值、负圈:
权值:边的距离, 负权值:边权是负的,负圈:图中的一个环,边权全部为负边权。
4、重边
相同的边,就比如 1->2 权值为3,数据中又出现 1->2 权值为4。
5、松弛:
先给出一张无向图
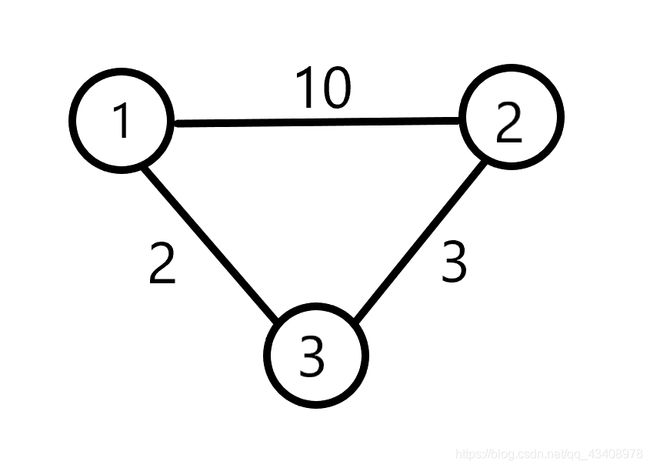
城市1到城市2有一条路长为10
城市1到城市3有一条路长为2
城市2到城市3有一条路长为3
现在要问城市1到城市2的最短距离是多少?
显然…答案是5,肉眼可以轻易看出来,但如果图一复杂,这种问题还是交给代码解决来的高效。
专业术语解这题 :
源是1,用dis[i]表示源到各点的最短距离,ma[i][j]表示城市i到城市j的距离。
初始时:dis[1] = 0; dis[2] = 10; dis[3] = 2;
ma[1][2] = ma[2][1] = 10; ma[1][3] = ma[3][1] = 2;
ma[2][3] = ma[3][2] = 3;
我们的目标是更新这个dis数组,让它成为真正的最短路径。暴力枚举后会找到一个式子dis[2] > dis[3] + ma[3][2],则更改dis[2] = dis[3] + ma[3][2],这一步,就是松弛。
在下列算法中宏定义V为点的数量,E为边的数量。
Floyd算法:多源、可以负边权、无负圈,时间复杂度V3 ,时间复杂度V2
这个算法就是直接把ma这个数组里的数据作为最短路径去松弛。
以hdu2544为例
#include<bits/stdc++.h>
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define pii pair<int, int>
using namespace std;
typedef long long ll;
template<class T>
void read(T &res) {
int f = 1; res = 0;
char c = getchar();
while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
res *= f;
}
const int N = 103;
const int INF = 0x3f3f3f3f; //相当于正无穷
int ma[N][N]; //i->j最短路径
int n, m; //点数、边数
int main() {
int u, v, w; // u - v 权值为w
while(scanf("%d%d", &n, &m), n+m) {
memset(ma, INF, sizeof(ma));
while(m--) {
read(u); read(v); read(w);
if(w < ma[u][v]) //防止有重边
ma[u][v] = ma[v][u] = w;
}
//开始暴力枚举,这里复杂度极高,后续算法大多是对这里进行优化
for(int k = 1; k <= n; ++k) {
for(int i = 1; i <= n; ++i) {
if(ma[i][k] == INF) continue; //剪枝
for(int j = 1; j <= n; ++j) {
if(ma[i][j] > ma[i][k] + ma[k][j]) { //松弛
ma[i][j] = ma[i][k] + ma[k][j];
}
//ma[i][j] = min(ma[i][j], ma[i][k] + ma[k][j]);
}
}
}
printf("%d\n", ma[1][n]);
}
return 0;
}
这个算法的优越性在于,它是多源的,并且可以处理无向图的最小环问题,大概就是在一个无向图中找出最小环的价值这样,对于松弛过的点,如果还能进行松弛就表示有环,运用这个特点,找最小环 。
以hdu1599为例
#include<bits/stdc++.h>
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define pii pair<int, int>
using namespace std;
typedef long long ll;
template<class T>
void read(T &res) {
int f = 1; res = 0;
char c = getchar();
while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
res *= f;
}
const int N = 110;
const int INF = 2e6; //因为爆精疯狂WA,调小一点
int mincycle, sum, n, m, dis[N][N], ma[N][N];
/*
mincycle表示最小环的价值,sum表示最小环的数量(跟这题没啥关系),n表示点数,m表示边数,
dis[i][j]表示i->j的最短路,ma存图
*/
void floyd() {
mincycle = INF;
for(int k = 1; k <= n; ++k) {
for(int i = 1; i < k; ++i) //更新最小环,以及更新最小环数量
for(int j = i+1; j < k; ++j) {
if(mincycle > dis[i][j] + ma[i][k] + ma[k][j])
{ mincycle = dis[i][j] + ma[i][k] + ma[k][j]; sum = 1; }
else if(mincycle == dis[i][j] + ma[i][k] + ma[k][j]) sum++;
}
for(int i = 1; i <= n; ++i) //路径还是要松弛的嘛
for(int j = 1; j <= n; ++j)
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
int main() {
int u, v, w;
while(~scanf("%d%d", &n, &m)) {
for(int i = 1; i <= n; ++i) //初始化
for(int j = 1; j <= n; ++j)
ma[i][j] = dis[i][j] = INF;
while(m--) {
read(u); read(v); read(w);
if(w < ma[u][v]) //防止重边
ma[u][v] = ma[v][u] = dis[u][v] = dis[v][u] = w;
}
floyd();
if(mincycle < INF) printf("%d\n", mincycle);
else puts("It's impossible.");
}
return 0;
}
dijkstra算法:单源,无负边权,时间复杂度是V2及以下,空间的话看具体优化。
这个算法需要用到dis数组,这个算法相对于上一个算法的优化就是,暴力枚举的时候每次选取dis值最小的点,而不是暴力枚举k,这样可以将其降到V2。
邻接矩阵(针对边多点少的情况)实现:以hdu2544为例
#include<bits/stdc++.h>
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define pii pair<int, int>
using namespace std;
typedef long long ll;
template<class T>
void read(T &res) {
int f = 1; res = 0;
char c = getchar();
while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
res *= f;
}
const int N = 1e3;
const int INF = 0x3f3f3f3f;
int ma[N][N], n;
int dis[N], vis[N];
//dis表示从起点到各个点的最短路,dis[i]表示s->i的最短路
//vis记录该点是否已经被松弛
void dij() {
int m = INF, mi;
for(int i = 1; i <= n; i++) { //先初始化dis数组
dis[i] = ma[1][i]; vis[i] = 0; //把dis中的值赋值为起点练得所有边的权值
}
dis[1] = 0; vis[1] = 1;
for(int j = 1; j <= n; j++) { //表示每个点都需要被松弛
m = INF; //初始化最小值
for(int i = 1; i <= n; i++) {
if(!vis[i] && dis[i] < m) {
//如果这个点没有被松弛,且这个点是以s为起点最小的
m = dis[i]; //就把找到的最小值的路径长赋值为该点
mi = i; //记录下该点是哪个点
}
}
vis[mi] = 1; //表示该点已经被松弛
for(int i = 1; i <= n; i++) {
if(!vis[i] && m + ma[mi][i] < dis[i]) { //若这个点没有松弛过且可以松弛
//如果最小值+以该最小值点为起点的路径长是不是小于以s为起点的路径长
dis[i] = m + ma[mi][i];
//更新dis数组
}
}
}
}
int main() {
int m, u, v, w;
while(scanf("%d%d", &n, &m), (n + m)) {
memset(ma, INF, sizeof(ma));
while(m--) {
read(u); read(v); read(w);
if(w < ma[u][v]) //防止有重边
ma[u][v] = ma[v][u] = w; //无向边
}
dij();
printf("%d\n", dis[n]);
}
return 0;
}
优先队列+结构体(针对点多边少的情况)实现:以hdu2544为例
#include<bits/stdc++.h>
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define pii pair<int, int> //dis, i
using namespace std;
typedef long long ll;
template<class T>
void read(T &res) {
int f = 1; res = 0;
char c = getchar();
while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
res *= f;
}
const int N = 103;
const int INF = 0x3f3f3f3f;
int n, m;
struct xx {
int to, cost;
};
int dis[N], vis[N];
vector<xx> v[N];
// v[i].to与v[i].cost分别表示 i -> to 这个点有一条边,花费为cost;
void dij() {
priority_queue< pii, vector<pii>, greater<pii> > q; //按照first升序排序
while(!q.empty()) q.pop();
dis[1] = 0; q.push(pii{0, 1});
//初始化列表方法把起始点放进优先队列
while(!q.empty()) {
//用一个优先队列存{dis[i], i} == s->i的距离 与 i
pii pp = q.top(); q.pop();
int vv = pp.second; //pp.second 表示当前需要松弛的点
if(vis[vv]) continue; //如果该点已被松弛, 循环继续
vis[vv] = 1; //松弛前把该点 标记为已被松弛
for(int i = 0; i < v[vv].size(); i++) { // 松弛过程
dis[v[vv][i].to] = min(dis[v[vv][i].to], v[vv][i].cost + dis[vv]);
q.push(pii{dis[v[vv][i].to], v[vv][i].to});
}
}
}
int main() {
int a, b, c;
while(scanf("%d%d", &n, &m), n+m) {
for(int i = 1; i <= n; ++i) { //跟邻接矩阵第一步相同,初始化dis数组
v[i].clear(); dis[i] = INF; vis[i] = 0;
}
while(m--) {
read(a); read(b); read(c);
v[a].push_back({b, c});
v[b].push_back({a, c});
}
dij();
printf("%d\n", dis[n]);
}
return 0;
}
优先队列+链式前向星优化:这个做法比较常用,是一个较优的算法,首先,前向星存图的方法,贴一个比较好理解一点的博客:链式前向星存图,以hdu2544为例
#include<bits/stdc++.h>
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define pii pair<int, int>
using namespace std;
typedef long long ll;
template<class T>
void read(T &res) {
int f = 1; res = 0;
char c = getchar();
while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
res *= f;
}
const int M = 1e4+4;
const int N = 103;
const int INF = 0x3f3f3f3f;
int n, m, s, t, cnt;
struct xx {
int next, to, w;
}edge[M];
//前向星存边的结构体
int vis[N], dis[N], head[N];
// vis常规记录该点是否已经松弛,dis常规记录源点到其他各点的距离,head是前向星存图的核心
priority_queue<pii, vector<pii>, greater<pii> > pq;
//优先队列优化
pii cur;
//松弛时简化代码使用
void add(int u, int v, int w) {
edge[cnt].w = w;
edge[cnt].to = v;
edge[cnt].next = head[u];
head[u] = cnt++;
}
//前向星加边
void dij() {
for(int i = 1; i <= n; ++i) { dis[i] = INF; vis[i] = 0; }
dis[1] = 0;
while(!pq.empty()) pq.pop();
pq.push(pii(dis[1], 1));
//常规初始化
while(!pq.empty()) {
cur = pq.top();
pq.pop();
if(vis[cur.second]) continue; //如果已经松弛过,跳过
vis[cur.second] = 1;
for(int i = head[cur.second]; i; i = edge[i].next) { //前向星访问边的基本形式
if(dis[edge[i].to] > cur.first + edge[i].w) { //松弛
dis[edge[i].to] = cur.first + edge[i].w;
pq.push(pii (dis[edge[i].to], edge[i].to)); //入队
}
}
}
}
int main() {
int u, v, w;
while(scanf("%d%d", &n, &m), n + m) {
cnt = 1;
memset(head, 0, sizeof(head));
for(int i = 1; i <= m; ++i) {
read(u); read(v); read(w);
add(u, v, w); add(v, u, w); //无向图存边形式
}
dij();
printf("%d\n", dis[n]);
}
return 0;
}
Bellman-Ford算法:单源,可以判断负环,时间复杂度VE。
这里实现一下打印路径,用一个pre数组保存当前节点的上一个节点,最后打印的时候用一个栈维护,比较好理解,代码量也很少。以hdu1224为例,嗯…然后我为了体现这个算法的突出之处,把板子总结了一下,所以这当中有个判断负环的步骤对这题是没用的。
#include<bits/stdc++.h>
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
using namespace std;
typedef long long ll;
template<class T>
void read(T &res) {
int f = 1; res = 0;
char c = getchar();
while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
res *= f;
}
const int N = 103;
const int INF = 0x3f3f3f3f;
struct xx {
int u, v, w;
}edge[N*N];
//结构体存边的形式实现,当然也可以用链式前向星实现...后续会提到
int n, m, a[N], dis[N], pre[N];
//点数,边数,a数组存每个城市的满足点,dis还是常规源点到各点的最短路,pre记录了当前节点的上一个节点。
int cnt, t;
//这个是为了题目要求的格式化..因为这个还P了一发
bool bellman_ford() {
bool f; int ok;
//f为了判断负环使用,ok是剪枝使用
for(int i = 1; i <= n + 1; ++i) dis[i] = -INF, pre[i] = 0;
dis[1] = 0; pre[1] = 1;
//常规初始化,让起点的pre值为自己
for(int i = 1; i <= n; ++i) { //每个点都要松弛一次
ok = 1;
for(int j = 1; j <= m; ++j) { //遍历边的形式
if(dis[edge[j].v] < dis[edge[j].u] + edge[j].w) { //松弛
dis[edge[j].v] = dis[edge[j].u] + edge[j].w;
pre[edge[j].v] = edge[j].u;
ok = 0;
}
}
if(ok) break; //如果当前没有边可以让点松弛,剪枝
}
f = 1; //这里在判断负环,跟floyd方法类似
for(int i = 1; i <= m; ++i) {
if(dis[edge[i].v] < dis[edge[i].u] + edge[i].w) {
f = 0; break;
}
}
return f;
}
//打印路径
void Print(int root) {
printf("CASE %d#\n", ++cnt);
printf("points : %d\n", dis[n+1]);
printf("circuit : ");
if(root == 2) printf("1\n");
else {
stack<int> sk; //用栈维护
while(!sk.empty()) sk.pop();
while(root != pre[root]) {
sk.push(root);
root = pre[root];
}
if(root == pre[root]) sk.push(root);
while(sk.size() > 1) { printf("%d->", sk.top() == n + 1 ? 1 : sk.top()); sk.pop(); }
if(sk.size() == 1) printf("%d\n", sk.top() == n + 1 ? 1 : sk.top());
if(cnt < t) puts(""); //控制格式
}
}
int main() {
read(t);
int u, v;
for(int k = 1; k <= t; ++k) {
read(n);
for(int i = 1; i <= n; ++i) {
read(a[i]);
}
a[n+1] = 0;
read(m);
for(int i = 1; i <= m; ++i) {
read(u); read(v);
if(u > v) swap(u, v); //这里指定了只能从小节点城市向大节点城市旅游
if(u == v) continue;
edge[i].u = u; edge[i].v = v; edge[i].w = a[v];
}
bellman_ford();
Print(n+1);
}
return 0;
}
spfa:单源,可以检测负圈,是Bellman-Ford的队列优化,不稳定,时间复杂度kE (k << V),不过最坏的情况还是会到达VE,只是大大优化了Bellman-Ford的复杂度
这个!我见过的最多!其次就是Dijsktra!
这里实现我用了前向星优化,以hdu2544为例
#include<bits/stdc++.h>
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
using namespace std;
typedef long long ll;
template<class T>
void read(T &res) {
int f = 1; res = 0;
char c = getchar();
while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
res *= f;
}
const int N = 103;
const int INF = 0x3f3f3f3f;
struct Node { //前向星结构体
int to, next, w;
//to 表示v, next里面跟u相同的边有关,w是u,v的距离
}edge[N*N];
int vis[N], outqueue[N], head[N], dis[N];
//outqueue关键是用来检测有没有负环出现,vis是常规操作,防止重复推进队列,标记..,head[i]是前向星中u = i这个点存在的最后一条边
int n, m, cnt;
void add(int u, int v, int w) { //前向星关键
edge[cnt].w = w;
edge[cnt].to = v;
edge[cnt].next = head[u];
head[u] = cnt++;
}
bool spfa() {
for(int i = 1; i <= n; ++i) {
dis[i] = INF; vis[i] = 0;
}
dis[1] = 0; vis[1] = 1;
queue <int> q;
q.push(1);
int cur;
while(!q.empty()) {
cur = q.front();
q.pop();
vis[cur] = 0; outqueue[cur]++;
if(outqueue[cur] > n) return false; // 负环出现
for(int i = head[cur]; i; i = edge[i].next) { //前向星的循环方式
if(dis[edge[i].to] > dis[cur] + edge[i].w) { //松弛
dis[edge[i].to] = dis[cur] + edge[i].w;
if(!vis[edge[i].to]) {
vis[edge[i].to] = 1; q.push(edge[i].to);
}
}
}
}
return true;
}
int main() {
int u, v, w;
while(scanf("%d%d", &n, &m), n + m) {
memset(head, -1, sizeof(head));
memset(outqueue, 0, sizeof(outqueue));
cnt = 1;
while(m--) {
read(u); read(v); read(w);
add(u, v, w);
add(v, u, w); //无向图
}
if(spfa()) {
printf("%d\n", dis[n]);
} else printf("have negative circle\n"); //有负环,跟这题没有这种情况
}
return 0;
}
啊,终于填完了这个坑,但是!没有差分约束的最短路是不完整的,但是如果了解了最短路,差分约束很好理解。
差分约束
大致题意:给出几个不等式条件,要得到某个不等式条件
描述:有这样一组不等式
{ x 1 − x 2 ≤ y 1 x 2 − x 3 ≤ y 2 x 3 − x 4 ≤ y 3 ⋯ x i − x j ≤ y k \begin{cases} x_1-x_2\leq y_1\\ x_2-x_3\leq y_2 \\ x_3-x_4\leq y_3 \\ \cdots \\ x_i-x_j\leq y_k \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧x1−x2≤y1x2−x3≤y2x3−x4≤y3⋯xi−xj≤yk
要根据这些关系计算出 x n − x 1 ≤ ? x_n-x1\leq ? xn−x1≤?
这样的问题可以转化为最短路方法解决,看到这些不等式,有没有想起来最短路里面的松弛,最简单的差分约束,就是一个三角形了,两边之和一定大于第三边,可以转化为上述的等式。目前制作过差分约束的水题,只要找到不等式,建边求最短路或者最长路就可以完成这道题了。
一般有两种形式,一种是像上面的<=,还有一种是>=。
<= :建边方式 x2->x1建立一条边权为y1的边,x3->x2建立一条边权为y2的边…xj->xi建立一条边权为yk的边,然后用这些边去求x1->xn的最短路。
>= :建边方式 x2->x1建立一条边权为y1的边,x3->x2建立一条边权为y2的边…xj->xi建立一条边权为yk的边,然后用这些边去求x1->xn的最长路。
以及有时候会出现既有>=号又有<=号的情况,看问题是要求啥,可以进行相应的转换,例如 4-3>=1 可以转化为 3-4<=-1,所以大部分差分约束问题都是用spfa解决的,因为可能包含负边权。
以hdu1384为例
这题就可以转化为差分约束来求解
#include<bits/stdc++.h>
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define pii pair<int, int>
using namespace std;
typedef long long ll;
template<class T>
void read(T &res) {
int f = 1; res = 0;
char c = getchar();
while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
res *= f;
}
const int N = 2e5+5;
const int INF = 0x3f3f3f3f;
struct xx {
int next, to, w;
}edge[N];
int n, cnt;
int vis[N], dis[N], head[N];
void add(int u, int v, int w) {
edge[cnt].w = w;
edge[cnt].to = v;
edge[cnt].next = head[u];
head[u] = cnt++;
}
//spfa方法求最短路
void spfa(int start, int ed) {
memset(dis, -INF, sizeof(dis));
memset(vis, 0, sizeof(vis));
queue<int> pq;
int cur;
dis[start] = 0; vis[start] = 1;
pq.push(start);
while(!pq.empty()) {
cur = pq.front();
pq.pop();
vis[cur] = 0;
for(int i = head[cur]; ~i; i = edge[i].next) {
if(dis[edge[i].to] < dis[cur] + edge[i].w) {
dis[edge[i].to] = dis[cur] + edge[i].w;
if(!vis[edge[i].to]) {
vis[edge[i].to] = 1;
pq.push(edge[i].to);
}
}
}
}
}
int main() {
int u, v, w, mx, mi;
while(~scanf("%d", &n)) {
cnt = 1; mx = 0; mi = INF;
memset(head, -1, sizeof(head));
for(int i = 1; i <= n; ++i) {
read(u); read(v); read(w);
add(u, v+1, w);
//列出不等式加边
mx = max(mx, v+1); mi = min(mi, u);
}
for(int i = mi; i < mx; ++i) {
add(i, i+1, 0); add(i+1, i, -1);
//这里是隐含条件,好好想想噢
}
spfa(mi, mx);
printf("%d\n", dis[mx]);
}
return 0;
}
真·水题!都是hdu的 0.0
基础最短路系列:
- 2544 最短路
- 1548 A strange lift
- 3790 最短路径问题
- 2066 一个人的旅行
- 2112 HDU Today
- 1874 畅通工程续
- 1217 Arbitrage
- 1869 六度分离
- 1690 Bus System
- 2722 Here We Go(relians) Again
- 1599 find the mincost route (floyd找最小环)
- 1224 free DIY Tour(输出路径)
差分约束系列:
- 1384 Intervals
- 1531 King
- 3440 House Man
- 3592 World Exhibition
终于填完了这个坑,马上要开学了,内心是拒绝的,就不能让我多躺两天 ,还要继续努力鸭~