Codeforces Round #641 (Div. 2) C. Orac and LCM（gcd和lcm的重要理解）

传送门

---

实际上不难发现序列中a₁对应的lcm对为n-1对，a₂对应的n-2对…以此类推，关键是如何化简如下的表达式：

gcd { lcm(a₁,a₂)，lcm(a₁,a₃)，…，lcm(a₁,a_n) }

---

GCD和LCM在质因数分解下的意义

假设a经过质因数分解后为P₁^k1*P₂^k2,…*P_n^kn，b经过质因数分解为Q₁^t1*Q₂^t2,…*Q_m^tm

假设质因子p为a和b共有的质因子，在a中p的幂次为k₁，在b中p的幂次为k₂，又因为所有的质因子两两互质，互不影响

那么gcd(a,b)的质因子p实际上的幂次为min{ k₁,k₂ }，lcm(a,b)的质因子p实际上的幂次为max{ k₁,k₂ }

---

那么现在我们再看上式，对于所有数的一个公共的质因子p，假设幂次分别为k₁,k₂,…k_n，上式的意义为：

min { max(k₁,k₂)，max(k₁,k₃)，…，max(k₁,k_n) }

然后该式等价于：

max { k₁，min {k₂,k₃,…,k_n) } }

即化为表达式：

lcm { k₁，gcd { k₂,k₃,…,k_n } }

因此我们得到等式：

gcd { lcm(a₁,a₂)，lcm(a₁,a₃)，…，lcm(a₁,a_n) } = lcm { k₁，gcd { k₂,k₃,…,k_n } }

其它收获

得知上述等式后，我们对左边和右边lcm化gcd得到：

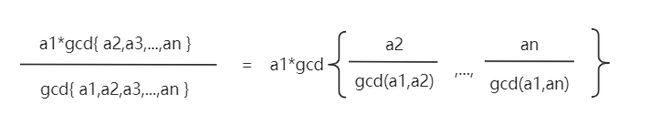
然后两边约去a₁：

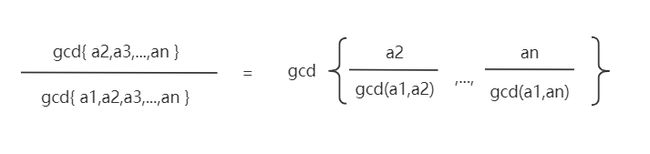
对于左式的分母，等价于gcd{ a₁,gcd{ a₂,a₃,…,a_n } }，那么我们将a₁看做x，将gcd{ a₂,a₃,…,a_n }看作y，那么左式实际上变成了：

y/gcd(x,y)

那么，实际意义就是将y和x相同的最大公因数从y中约去，而这时再看右式，不难发现实际就是将y中的每一部分与x相同的最大公因数约去，又因为gcd运算和乘法的交换性（即k*gcd(a,b)=gcd(k*a,k*b））最后再求gcd即约去了整体与x的最大公因数

---

最后对于本题，我们只需预处理后缀的gcd即可

PS:本题的公式还可用另外方法证明，见mrcrack的博客

#include <set>
#include <map>
#include <stack>
#include <queue>
#include <math.h>
#include <cstdio>
#include <string>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define lowbit(x) (x&(-x))
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const double eps=1e-8;
const double pi=acos(-1.0);
const int inf=0x3f3f3f3f;
const ll INF=1e18;
const int Mod=1e9+7;
const int maxn=2e5+10;

int a[maxn],sub[maxn];

ll gcd(ll a,ll b){
    return b==0?a:gcd(b,a%b);
}

ll lcm(ll a,ll b){
    return a/gcd(a,b)*b;
}

int main(){
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    sub[n]=a[n];
    for(int i=n-1;i>=1;i--)
        sub[i]=gcd(sub[i+1],a[i]);
    ll ans=0;
    for(int i=1;i<=n;i++)
        ans=gcd(ans,lcm(a[i],sub[i+1]));
    cout<<ans<<endl;
    return 0;
}