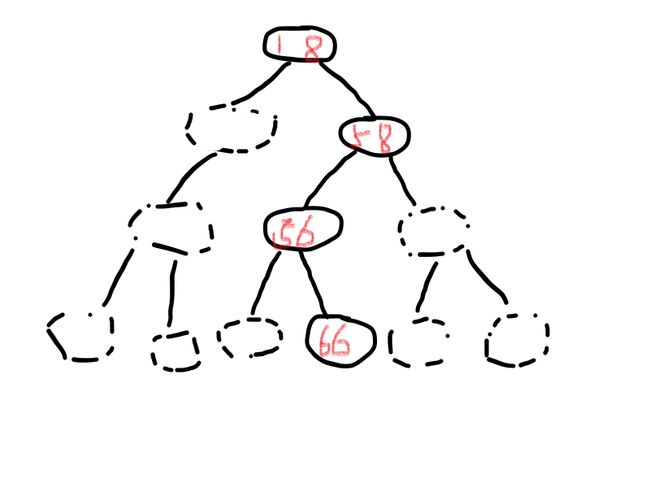
简介:
发现,有的时候,线段树需要维护的区间很大很大,但是实际用到的节点很少很少。
那么,我们干脆就不要开这么多的节点,用到的时候再向内存要。
也就是说,我们建立了一棵残疾的线段树,缺少很多枝叶,但是绝对够用了。
画个图大概理解一下(虽然也不太对)
实心边框的点都是我们申请内存给的,虚的点是没用的。就算申请也不用,实在是浪费资源。
所以,
我们开局只有一个根,
装备全靠给。
枝叶全靠给。
例如我们要建立一个权值线段树,但是在线操作不让你离散化,值域又是inf级别的,
像这样,即使这个区间的范围很大,但是如果询问q比较少的话,我们只需要qloginf个节点,就可以办到。
具体代码实现:
不同的操作,但是大同小异。
还是类似于一般线段树的。
框架:
function(int &x,int l,int r,int blablabla){
if(!x){
//建新节点,并处理信息
if(l==r) //叶子节点由于是真正要用的节点(对于单点),往往还要特殊记录信息
}
if(blablabla) return ???//判断是否能返回等等
(int ret) // 如果需要返回时停留更新信息,就弄一个ret
if(blablabla) return (t[x].ls,l,mid,blablabla)
if(blablabla) return (t[x].rs,mid+1,r,blablabla);
(pushup(x)) //回溯后更新
}
发现和主席树有点像,但是省空间的思想还是有些不同的。
主席树是:多棵线段树,利用相邻之间有很大部分是相同的。可以在之前线段树基础上建立线段树。
特点:许多线段树共用儿子节点
动态开点线段树:一棵线段树,利用实际用到的点不多,少开了很多节点。
特点:区间范围很大(通常不能直接开下)
共同点:(都是线段树)
都通过新加入的节点有限,进行的空间优化。使得时间空间复杂度都是logn/次
例题:(里面也有本篇的部分讲解)
NOIP2017 列队
upda:2018.9.22
主席树相邻的有很大的关系,那么动态开点线段树呢?
动态开点线段树也可以支持合并。
函数:
int merge(int x,int y,int l,int r){
if(!x||!y) return x|y;
if(l==r){
do something on the leaf
}
else{
t[x].ls=merge(t[x].ls,t[y].ls,l,mid);
t[x].rs=merge(t[x].rs,t[y].rs,mid+1,r);
pushup(x);
}
return x;
}
理解:空节点直接返回,然后本质其实是相当于利用y的儿子们,修改x儿子们的信息。
同样也是会达到共用儿子的目的。
注意叶子节点的特判暴力合并。
其实类似左偏树的合并。
但是复杂度的原理证明不太相同。
这个merge的证明主要是通过,每成功合并一次,节点数会少1个。
如果开始有mlogn个节点,那么最多合并mlogn次,复杂度就可以保证。
空间复杂度:总共nlogn,也就是开始节点个数。
发现,其实我们把动态开点线段树和主席树联系起来了!
但是,主席树不能直接合并多棵(其实也可以,但就和动态开点线段树没区别了。),必须在一棵基础上建立,而且不能灵活支持修改。
动态开点线段树就可以支持一次次地合并多棵为一棵,但是同样,合并后,再修改就比较麻烦了。
例题:
[Vani有约会]雨天的尾巴——树上差分+动态开点线段树合并
upda:2018.11.1
根据上面两个题的做法,
动态开点线段树,还经常开很多棵,
对于某个点要打很多不同的标记,并且父子之间标记要快速合并的话,
那么每个点动态开点线段树就比较优秀了。
(相较于一般的差分只是差分一种标记,这个就比较强大了。)
甚至:
天天爱跑步——树上差分
这个题用个动态开点线段树直接打差分标记也是可以的。。。(如果你不会全局桶的骚操作的话)