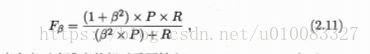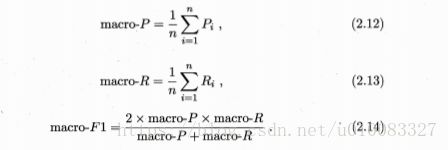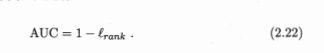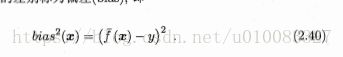《机器学习（周志华）》Chapter2 模型评估与选择

    这一章几乎把整个机器学习的工作流程都介绍了一遍，能让读者了解到如何一步步的搭建一个机器学习项目。下面先把整个流程大致的梳理一遍：

一、评估方法：

我们在拿到数据之后首先要处理的就是将数据划分为训练集和测试集，西瓜书提供了三种方法，分别是：留出法、交叉验证法和自助法。

1、留出法：将数据集划分为两个互斥的集合，将70%划分为训练集，30%划分为测试集。如果我们希望评估的是整个训练集的模型性能，而留出法将整体数据集划分为训练集合测试集，若训练集包含绝大多数样本，则训练出的模型可能更接近整体数据的模型，而测试集符合的样本比较少，评估的结果可能就不稳定准确；若测试集多包涵一些样本，则训练集合整体样本差别就更大，训练出的模型与整体训练处的模型相差较大，从而降低了评估结果的保真性。

2、交叉验证法：将数据集划分成k个大小相同的互斥子集，将k-1个子集的并集作为训练集，剩余的一个子集作为测试集，最后求k组训练测试集的均值。

3、自助法：如果我们希望评估的是整体数据集，用留出法或交叉验证法，都会导致训练集变小，为解决这个问题就引入了自助法。若有m个样本的数据集，从数据集中采样一个样本放入另外一个集合，再将该样本放回原数据集，重复m次，就采用到了另外一个大小也为m的集合，将这个集合作为训练集，原数据集除开新集合剩余的数据作为训练集，称为自助法。自助法在小数据集和集成学习上有很大的好处，但是改变了原数据集的分布，会引入估计偏差，所以在数据量足够时，留出法和交叉验证法还是常用一些。

二、调参与最终模型

三、性能度量

模型训练完之后最终要应用到现实任务上，这就需要知道训练好的模型的泛化能力如何，这就是性能度量。

1、错误率与精度

错误率：

精度：

或者：

2、查准率、查全率与F1：

不同重视程度下的F1：

其β>0，度量了查全率对查准率的相对重要性。β=1为标准的F1；β>1查全率影响更大；β<1查准率影响更大。

对多个查准率、查全率求平均称为宏查准率、宏查全率、宏F1：

对TP、FP、TN、FN求平均值，再计算称为微查准率、微查全率和微F1:

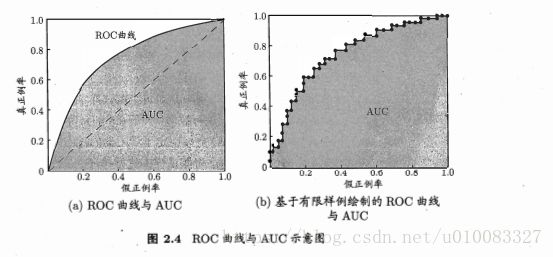
3、ROC与AUC

TPR真正例率、FPR假正例率

绘图过程：给定m+个正例和m-个反例，根据学习器预测结果对样例排序，若将分类阀值设为最大，即所有样本均为反例，则TP和FP均为零，即得坐标（0,0），若分类阀值设为最小，即所有样本均为正例，则FN和TN均为零，即得坐标（1,1）。将分例阀值从最大值依次减小为每个样本大小，即依次将每个样本划分为正例，设前一个坐标为（x,y），若当前样本预测为真正例，因为TP+FN始终等于m+，所以增加一个真正例即纵坐标增加1/m+，则对应坐标为(x, y+1/m+),同理若为假正例，对应坐标为（x+1/m-, y），然后用线段将相邻点依次相连就形成了ROC曲线

AUC为ROC曲线下的面积，AUC越大性能越好。

排序损失定义为：

正例的预测值小于反例，记一个罚分，正例等于反例记0.5个罚分。

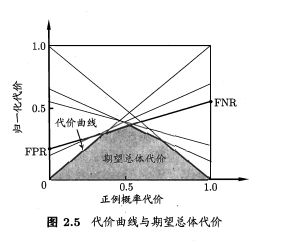
4、代价敏感错误率与代价曲线

解决不同类型的错误造成不同的后果，衍生出了代价敏感错误率。

代价敏感错误率为：

cost01大于cost10,0类判别为1类所造成的损失更大；

正例概率代价为：

其中p是样例为正例的概率；归一化代价：

四、比较检验

先使用某种实验评估方法测得学习器的某个性能度量结果，然后对结果进行比较。但是这个比较不是简单的比较过程，第一、我们希望比较的是泛化性能，泛化性能与测试集性能未必相等；第二、测试集的性能与选择有关；第三、很多机器学习算法本身有一定的随机性。

1、假设验证

简单的介绍一下假设验证，以抛硬币为例，如果我们想通过硬币来进行赌博，但我们不知道硬币是否是正常的，也就是说不知道对方有没有在硬币上做手脚让自己获胜的概率大一些，但是对方又不答应将硬币给我们检查，该如何判断硬币是否正常呢？我们可以假设硬币没有问题，然后进行试抛，如果抛一次是正面，概率为0.5，不足以证明硬币有无问题，抛两次都是正面，概率为0.25，也不足以说明；但是如果抛10次，全部都为正面，概率为0.5的10次方，我们就有一定的把我说这个硬币是有问题的。

首先根据测试错误率估推出泛化错误率的分布。泛化错误率为ε的学习器被测得测试错误率为ε的概率：

对进行假设验证，1-α为置信度

若测试错误率小于临界错误率，则得出结论：在α显著度下，假设成立，即能以1-α的置信度认为，学习器的泛化错误率不大于ε0

2、t检验

如果有多个测试错误率，则可以用t检验，平均测试错误率和方差为：

对假设和显著度α可以计算最大错误率，即临界值。在临界范围内假设成立，否则假设不成立。

交叉t检验：

5X2交叉验证：

3、McNemar检验

4、Friedman检验与Nemenyi后续检验

若在同一组数据集上对多个算法进行比较，则可使用该检验

五、偏差与方差：

学习算法的期望预测为：

方差：

噪声：

偏差：

《机器学习（周志华）》Chapter2 模型评估与选择 课后习题答案

参考网址：

假设检验
https://www.zhihu.com/question/23149768/answer/282842210
t检验
https://www.zhihu.com/question/30753175?sort=created

置信区间
https://www.zhihu.com/question/26419030/answer/274472266
95%置信区间
https://www.zhihu.com/question/23149768/answer/282842210
正态分布和t分布：
https://wenku.baidu.com/view/638df78c84868762caaed5fc.html