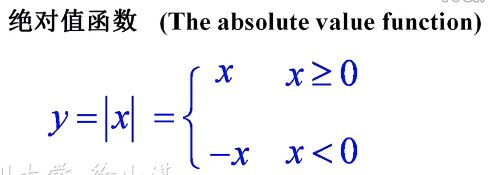高数(上)学习(1.1)——函数及其性质(中学复习篇)
1.1.1 集合
集合:具有某种特定性质事物的全体称为集合。
元素:组成这个集合的事物称为该集合的元素。
集合与元素的关系:属于∈,不属于∉。
不含任何元素的集合称为空集,记作∅。
集合的表示方法:列举法,描述法。
- 列举法:按某种方式列出集合中的全体元素。
- 描述法:M={ x | x所具有的特征 }
补充:两个整数互质(或互素)是指它们没有大于1的整数因子。
1.1.2 集合的运算
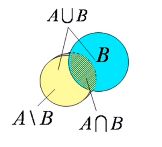
基本运算:并、交、差。
并集:A U B = { x | x∈A 或 x∈B }
交集:A ∩ B = { x | x∈A 且 x∈B }
差集:A \ B = { x | x∈A 且 x∉B }
全集\基本集:研究的问题所限定的大集合。
余集\补集:I - A或者AC 。
运算规律:交换律、结合律、分配律、对偶律、幂等律、吸收律。
1.1.3 区间与领域
有限区间:开区间(a,b) 闭区间[a,b] 半开区间[a,b) (a,b]。b-a:区间长度
无限区间:开区间(a,+∞) (-∞,a) -∞,+∞) 半开区间[a,+∞) (-∞,a]
邻域:以点x0为中心的任何开区间称为点x0的邻域,记作U(x0)。若δ是某一正数,则开区间(x0-δ,x0+δ)是点x0的一个邻域,记作U(x0,δ)。
左邻域:(x0-δ,x0)
右邻域:(x0,x0+δ)
1.1.4 映射
X,Y是两个非空集合,存在一个法则f,使得对X中的每个元素x,按法则f在Y中有唯一确定的元素y与之对应,则称f为X到Y的一个映射。
定义域D(f),值域R(f)或f(X)。
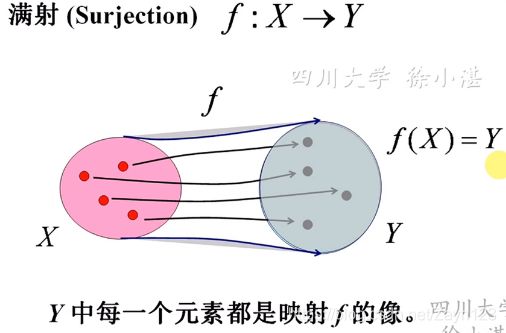
满射:
非满射:
单射:f(x1) ≠ f(x2)
在函数图像中,一个y值对应一个x值。
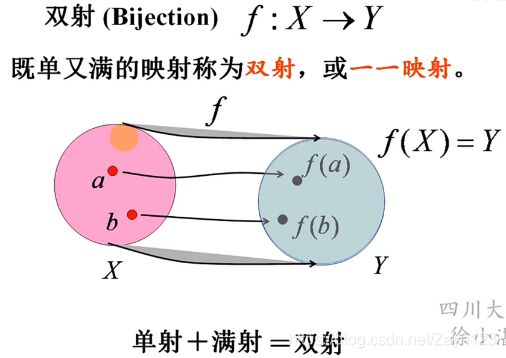
一 一映射:满射+单射
单射很重要:
- 每一个单射都可诱导一个双映射。
- 每一个单射也可以诱导一个逆映射。
泛函、变换、函数
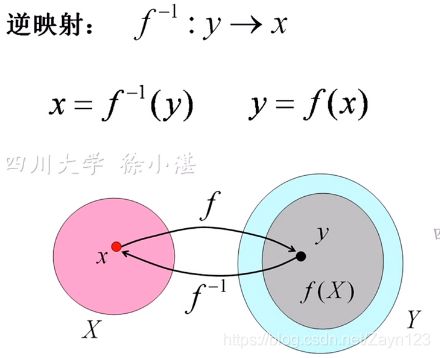
逆映射:g:R(f) -> X (f是单射,y = f(x),则 x = g(y))
复合映射:g:X->Y1,f:Y2->Z,Y1包含于Y2, f g:X->Z。
1.1.5 函数
D是实数集,称f:D->R为定义在D上的函数。y = f(x),x∈D。y是因变量,x是自变量,D称为定义域。\
1.1.6 几个分段函数
绝对值函数:
符号函数:
取整函数:向上取整、向下取整、向零取整
1.1.7 函数的三要素
(1)定义域
考点1:定义域(分母不为0、根号里非负数、真数大于0)
考点2:整体法求定义域
考点3:判断两个函数是否是同一函数
(2)函数关系
(3)值域
1.1.8 函数的特性
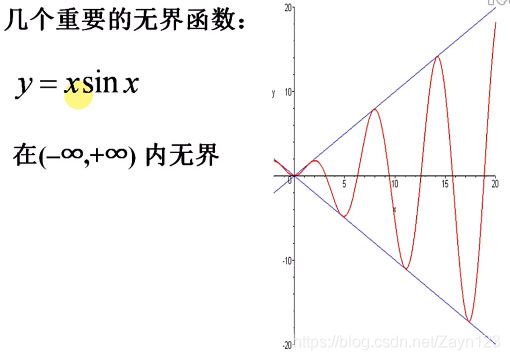
(1)函数的有界性
X包含于D,若存在M使得f(x) <= M,则称f(x)在X上有上界,类似可得下界的定义。数M使得|f(x)| <= M(x∈X),则称f(x)在X上有界。
注意:在求复合函数的时候,外函数有界,复合函数必有界。
(2)函数的单调性
区间I包含于D,若对于I上的任意两点x1,x2,当x1
(3)函数的奇偶性
定义域D关于原点对称,即若x∈D,则-x∈D。
若对任意的x∈D,都有f(x) = -f(-x),则称为奇函数;若对任意的x∈D,都有f(x) = f(-x),则称为偶函数。
偶函数:f(-x)=f(x)图像关于y轴对称
奇函数:f(-x)=-f(x)图像关于原点对称
(4)函数的周期性
定义域D,若存在一个整数T,使得对任意x∈D,有(x+-T)∈D,且恒成立,则称f(x)为周期函数。
f(x+T)=f(x),周期函数
1.1.9 反函数和复合函数
函数f:D->f(D)是单射,存在逆映射f-1:f(D)->D,称此映射为函数f的反函数。
若f是单调函数,则必存在反函数,且反函数也是单调函数。
一个函数有反函数的条件:它是一个单映射。
y=f(u),D(f),R(f) u=g(x) D(g),R(g) R(g)包含于D(f),复合映射确定的函数为复合函数。
1.1.10 函数的四则运算
和(差)f +- g:(f +- g)(x) = f(x) +- g(x),x∈D;
积 f * g:(f * g)(x) = f(x) * g(x),x∈D;
商 f / g:(f / g)(x) = f(x) / g(x),x∈D \ { x | g(x) = 0, x∈D };
1.1.11 初等函数
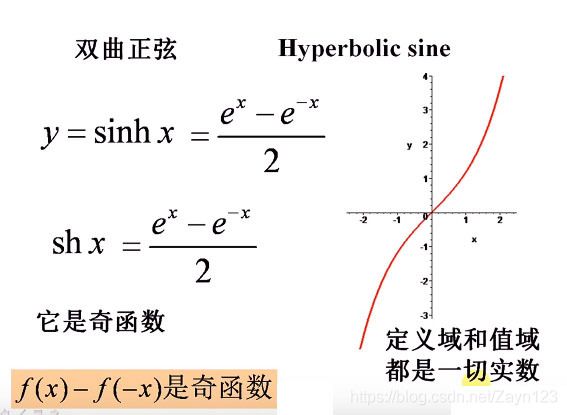
幂函数、质数函数、对数函数、三角函数、反三角函数、双曲正弦、双曲余弦、双曲正切、反双曲正弦、反双曲余弦、反双曲正切等。
不常见初等函数:
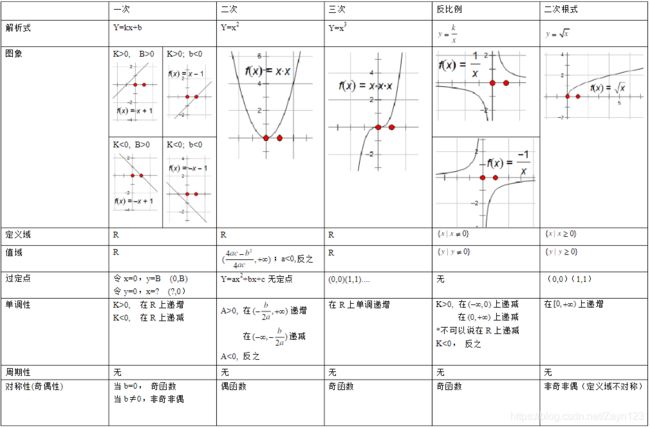
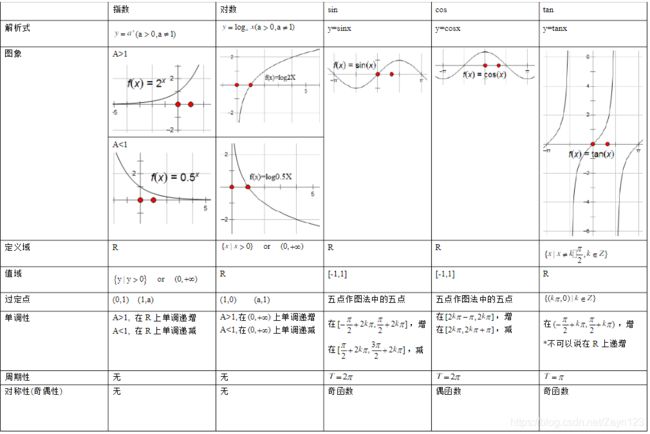
附常见基本初等函数: