Python Scikit-opt调包实践
今天看见原来Python也有相应的优化算法包scikit-opt,但安装时出现了问题,具体可见博客。
接下来就开始快乐的学习调包吧!
今天主要学习遗传算法和模拟退火算法实现,先对这两种算法做一个简单介绍。
遗传算法
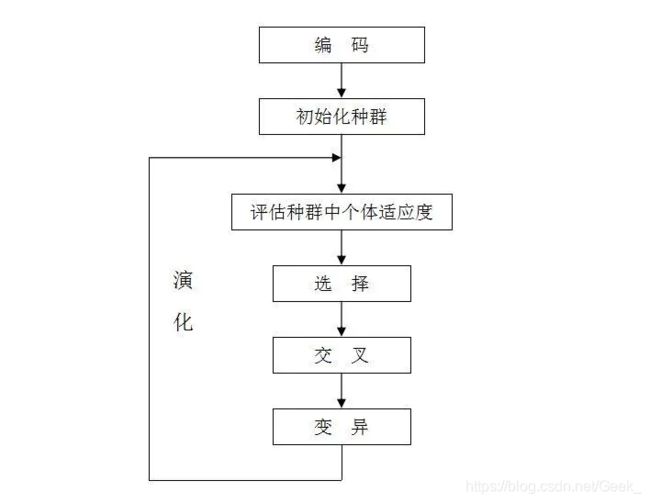
遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,不需要确定的规则就能自动获取和指导优化的搜索空间,自适应地调整搜索方向。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
遗传算法过程图解
模拟退火算法
为了解决局部最优解问题, 1983年,Kirkpatrick等提出了模拟退火算法(SA)能有效的解决局部最优解问题。我们知道在分子和原子的世界中,能量越大,意味着分子和原子越不稳定,当能量越低时,原子越稳定。‘退火’是物理学术语,指对物体加温在冷却的过程。模拟退火算法来源于晶体冷却的过程,如果固体不处于最低能量状态,给固体加热再冷却,随着温度缓慢下降,固体中的原子按照一定形状排列,形成高密度、低能量的有规则晶体,对应于算法中的全局最优解。而如果温度下降过快,可能导致原子缺少足够的时间排列成晶体的结构,结果产生了具有较高能量的非晶体,这就是局部最优解。因此就可以根据退火的过程,给其在增加一点能量,然后在冷却,如果增加能量,跳出了局部最优解,这本次退火就是成功的。
模拟退火的步骤:
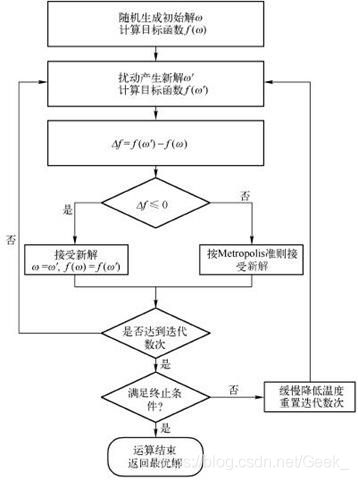
1.模拟退火算法可以分解为解空间、目标函数和初始解三部分。
2.模拟退火的基本思想:
(1) 初始化:初始温度T(充分大),初始解状态S(是算法迭代的起点),每个T值的迭代次数L
(2) 对k=1, …, L做第(3)至第6步:
(3) 产生新解S′
(4) 计算增量ΔT=C(S′)-C(S),其中C(S)为代价函数
(5) 若ΔT<0则接受S′作为新的当前解,否则以概率exp(-ΔT/T)接受S′作为新的当前解.
(6) 如果满足终止条件则输出当前解作为最优解,结束程序。
终止条件通常取为连续若干个新解都没有被接受时终止算法。
(7) T逐渐减少,且T->0,然后转第2步。
流程图
调包时刻
首先对于jupyter使用小技巧记录下,原先一直都是通过Anaconda直接打开,但这样目录就固定了,对于需要写多个不同程序就会很不方便,因此,可以采用下面方法,在需要放代码的目录下,打开cmd窗口,输入
jupyter notebook
即可在当前目录工作。
遗传算法
首先定义目标函数
def demo_func(p):
'''
This function has plenty of local minimum, with strong shocks
global minimum at (0,0) with value 0
'''
x1, x2 = p
x = np.square(x1) + np.square(x2)
return 0.5 + (np.sin(x) - 0.5) / np.square(1 + 0.001 * x)
用遗传算法求解
from sko.GA import GA
import numpy as np
#2个变量,每代取50个,800次迭代,上下界及精度
ga = GA(func=demo_func, n_dim=2, size_pop=50, max_iter=800, lb=[-1, -1], ub=[1, 1], precision=1e-7)
best_x, best_y = ga.run()
print('best_x:', best_x, '\n', 'best_y:', best_y)
模拟退火算法
首先定义目标函数
def demo_func(x):
x1, x2, x3 = x
return x1 ** 2 + (x2 - 0.05) ** 2 + x3 ** 2
- Fast Simulated Annealing
from sko.SA import SAFast
sa_fast = SAFast(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_fast.run()
print('Fast Simulated Annealing: best_x is ', sa_fast.best_x, 'best_y is ', sa_fast.best_y)

2. Boltzmann Simulated Annealing
from sko.SA import SABoltzmann
sa_boltzmann = SABoltzmann(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_boltzmann.run()
print('Boltzmann Simulated Annealing: best_x is ', sa_boltzmann.best_x, 'best_y is ', sa_fast.best_y)
from sko.SA import SACauchy
sa_cauchy = SACauchy(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_cauchy.run()
print('Cauchy Simulated Annealing: best_x is ', sa_cauchy.best_x, 'best_y is ', sa_cauchy.best_y)