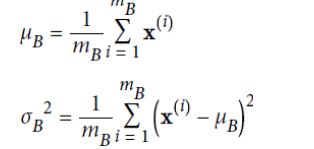【深度学习篇】--神经网络中解决梯度弥散问题
一、前述
在梯度下降中,随着算法反向反馈到前面几层,梯度会越来越小,最终,没有变化,这时或许还没有收敛到比较好的解,这就是梯度消失问题,深度学习遭受不稳定的梯度,不同层学习在不同的速度上
二、解决梯度弥散和消失方法一,初始化权重使用he_initialization
1、举例
如果我们看逻辑激活函数,当输入比较大,不管正负,将会饱和在0或1,这样梯度就是0,因此当反向传播开始,它几乎没有梯度传播回神经网络,所以就会导致只更改高的几层,低的几层不会变化,这就是为什么替代Relu函数的原因。
2、初始化
我们需要每层输出的方差等于它的输入的方差,并且我们同时需要梯度有相同的方差,当反向传播进入这层时和离开这层,方差也一样。
上面理论不能同时保证,除非层有相同的输入连接和输出连接,
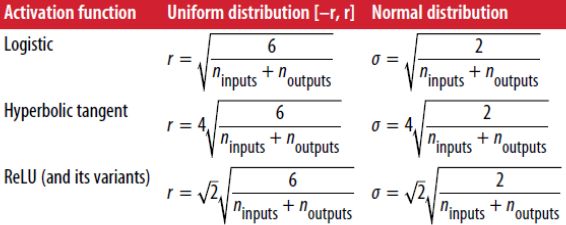
但是有一个不错的妥协在实际验证中,连接权重被随机初始化,n_inputs和n_outputs是输入和输出的连接,也叫fan_in和fan_out,
这种初始化的策略叫Xaiver initialization
3、具体应用
看输入和输出的连接数找到对应公式计算半径来随机初始化权重,是最合理的,是最不容易产生梯度弥散的初始化权重。
4、He Initialization(变形的Relu激活函数)
初始化策略对应ReLU激活函数或者它的变形叫做He initialization
fully_connected()函数默认使用Xavier初始化对应uniform distribution(full_connected默认会初始化参数和bias)
我们可以改成He initialization使用variance_scaling_initializer()函数,如下
三、解决梯度弥散问题方法二,使用不饱和激活函数解决单边抑制
1、场景
选择ReLU更多因为对于正数时候不饱和,同时因为它计算速度快
但是不幸的是,ReLU激活函数不完美,有个问题是dying ReLU,在训练的时候一些神经元死了。
2、解决方法
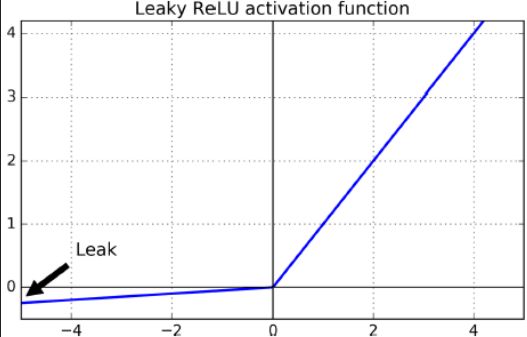
当它们输出小于0,去解决这个,使用leaky ReLU,max(a*z,z),a=0.01,在乎运行性能速度,可以试试
3、常用不饱和激活函数
leaky ReLU a是一个固定的值,需要手动实现
RReLU,Random,a是一个在给定范围内随机取值的数在训练时,在测试的时候取a得平均值,过拟合
可以试试
PReLU,Parametric,a是一个在训练过程中需要学习的超参数,它会被修改在反向传播中,适合
大数据集
ELU,exponential,计算梯度的速度会慢一些,但是整体因为没有死的神经元,整体收敛快,超参
数0.01(实际中用的不多),解决零点不可导的问题,ELU可以直接使用。
![]()
选择激活函数结论:
ELU > leaky ReLU > ReLU > tanh > logistic
四、解决梯度弥散方法三,利用Batch Normalization
1、场景
尽管使用He initialization和ELU可以很大程度减少梯度弥散问题在一开始训练,但是不保证在训练的后面不会发生
Batch Normalization可以更好解决问题。它应用于每层激活函数之前,就是做均值和方差归一化,对于每一批次数据并且还做放大缩小,平移,为了梯度下降的时候收敛的时候速度更快。
相当于把数据都拉到中间的位置了,有这个就不需要Dropout,Relu等等
2、本质
本质就是均值,归一化,放大,缩小
![]()
3、具体使用原理
在测试时,使用全部训练集的均值、方差,在Batch Normalization层,总共4个超参数被学习,
scale,offset,mean,standard deviation。
scale,offset,如下
mean,standard deviation。如下,B是每一批次
利用Batch Normalization即使是用饱和的激活函数,梯度弥散问题也可以很好减轻
利用Batch Normalization对权重初始化就不那么敏感了,用不用he_initlinze无所谓了,但最好用
利用Batch Normalization可以使用大一点的学习率来提速了。
利用Batch Normalization同样的准确率,4.9% top-5错误率,速度减少14倍
利用Batch Normalization也是一种正则化,就没必要使用dropout了或其他技术了
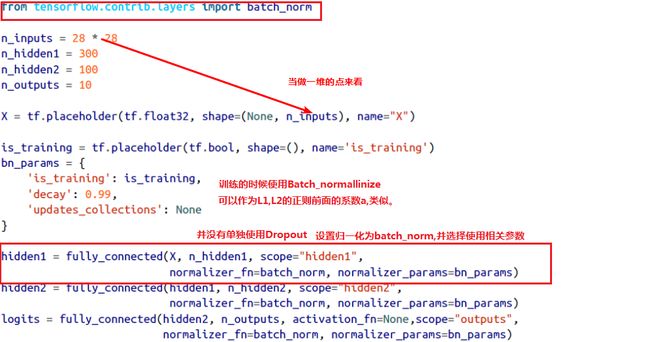
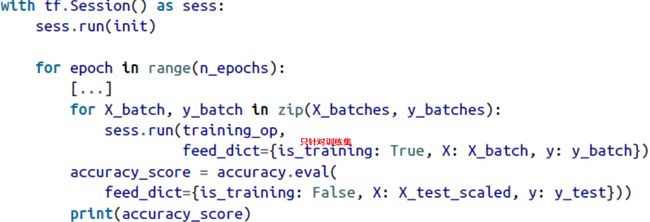
3、具体使用代码
4、代码优化
真正运行的时候代码如下: