- 文本识别论文大全
CV小蜗牛
文本识别文本识别ocr代码计算机视觉深度学习
文本识别论文*CODE表示官方代码CODE表示非官方代码具体详见github,欢迎star,fork,pr,issue等Conf.DateTitleHighlightcodeAAAI2022TextGestalt:Stroke-AwareSceneTextImageSuper-ResolutionAttention*CODEAAAI2022VisualSemanticsAllowforTextua
- 【重磅整理】180篇NIPS-2020顶会《强化学习领域》Accept论文大全
深度强化学习实验室
人工智能强化学习xhtml微软敏捷开发
深度强化学习实验室作者:《DeepRL-Lab》&《AMiner.cn》联合发布来源:https://neurips.cc/Conferences/2020/编辑:DeepRL(图片来自新智元)NeurIPS终于放榜,提交数再次创新高,与去年相比增加了38%,共计达到9454篇,总接收1900篇,其中谷歌以169篇傲视群雄,清华大学63篇,南京大学周志华教授团队3篇。论文接收率20.09%较去年有
- 什么?语音合成开源代码不会跑,follow me!
摘要:本文描述的深度神经网络模型结构::NaturalTTSsynthesisbyconditioningWavenetonMELspectogrampredictions。本文分享自华为云社区《什么?语音合成开源代码不会跑,我来教你跑Tacotron2》,作者:白马过平川。Tacotron-2:TTS论文大全:https://github.com/lifefeel/S... DeepMind的
- 【重磅整理】180篇NeurIPS2020顶会《强化学习领域》Accept论文大全
AMiner科技
AMiner会议论文推荐自然语言处理神经网络机器学习深度学习数据挖掘
NeurIPS终于放榜,提交数再次创新高,与去年相比增加了38%,共计达到9454篇,总接收1900篇,其中谷歌以169篇傲视群雄,清华大学63篇,南京大学周志华教授团队3篇。论文接收率20.09%较去年有所下降,其中论文主题占比和结构图如下:算法(29%)深度学习(19%)强化学习(9%)作者:《DeepRL-Lab》&《AMiner.cn》联合发布来源:https://neurips.cc/C
- 《元学习meta learning)》2020综述论文大全!
Mr.Jk.Zhang
深度学习
【导读】元学习旨在学会学习,是当下研究热点之一。最近来自爱丁堡大学的学者发布了关于元学习最新综述论文《Meta-LearninginNeuralNetworks:ASurvey》,值得关注,详述了元学习体系,包括定义、方法、应用、挑战。成为不可缺少的文献。近年来,元学习领域,或者说“学会学习的学习”,引起了人们极大的兴趣。与传统的人工智能方法(使用固定的学习算法从头开始解决给定的任务)不同,元学习
- 行人检测论文大全
Ddreaming
行人检测
行人检测论文汇总马上就研二了,压力山大,回想研一整个一年,忙忙碌碌,却没出什么成绩,真是。。回首研一,可能就做了一点点工资,学习一些基本知识,比如常用机器学习算法、opencv、图像处理等等,然后开始接触行人检测,读dollar大神的论文,读他的工具包等等,现在感觉有点入门了,下面是dollar大神整理的资源,里面有行人检测领域最新最经典的论文,准备利用一两个月把这些经典的论文都读一读,原文地址:
- 【HC3i电子病历论文大全】截止2010年8月19日共计95篇
紫凝
生活职场休闲HC3i
帖子中包含了目前HC3i资源版块中关于电子病历的所有论文精选(截止到2010年8月19日),目的主要是方便需要电子病历的用户查找相关论文。由于我本身对电子病历论文分类不是很擅长,所以,仅仅是汇总而已,也许有一些论文是废话,也许有一些论文甚至观点是错的,这些我都不能保证。以下精选电子病历论文基本都是网友上传,至于附件质量,我也不能全部保证,大家还是有选择的下载,下载自己真正需要的资料。也许这几个专题
- 毕业论文大全 (本科)
sunlzx
.net教育读书asp.netasp
毕业论文大全 (本科)
分享
陈文江 昨天 21:50分享
毕业论文大全,暂时用不到你也留着,不然四、五月你着急吧
不要希望在网上可以免费找到你的毕业论文(除非你论文答辩不想过了),更不要觉得下面东西没用,当你做论文时最快的帮你找到资料、文献.
[
http://www.51lw.com (免费论文下载)
http://www.teachercn
- 项目管理与项目经理
lcj8
工作项目管理活动工具任务Motorola
项目管理与项目经理 [论文大全-经济学论文]【打印】【字体:大 中 小】 项目管理与项目经理2001-07-31一、项目管理的产生与发展项目是一种一次性的工作,它应当在规定的时间内,在明确的目标和可利用资源的约束下,由专门组织起来的人员运用多种学科知识来完成。美国项目管理学会PMI(Project Management Instiute)对项目的定义是:将人力资源和非人力资源结合成一个短期组织以
- 项目管理与项目经理
逆风的香1314
工作项目管理活动招聘电信
项目管理与项目经理 [
论文大全 -
经济学论文]
【打印】 【字体:
大
中
小】 项目管理与项目经理
2001-07-31
一、项目管理的产生与发展
项目是一种一次性的工作,它应当在规定的时间内,在明确的目标和可利用资源的约束下,由专门组织起来的人员运用多种学科知识来完成。美国项
- java数字签名三种方式
知了ing
javajdk
以下3钟数字签名都是基于jdk7的
1,RSA
String password="test";
// 1.初始化密钥
KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("RSA");
keyPairGenerator.initialize(51
- Hibernate学习笔记
caoyong
Hibernate
1>、Hibernate是数据访问层框架,是一个ORM(Object Relation Mapping)框架,作者为:Gavin King
2>、搭建Hibernate的开发环境
a>、添加jar包:
aa>、hibernatte开发包中/lib/required/所
- 设计模式之装饰器模式Decorator(结构型)
漂泊一剑客
Decorator
1. 概述
若你从事过面向对象开发,实现给一个类或对象增加行为,使用继承机制,这是所有面向对象语言的一个基本特性。如果已经存在的一个类缺少某些方法,或者须要给方法添加更多的功能(魅力),你也许会仅仅继承这个类来产生一个新类—这建立在额外的代码上。
- 读取磁盘文件txt,并输入String
一炮送你回车库
String
public static void main(String[] args) throws IOException {
String fileContent = readFileContent("d:/aaa.txt");
System.out.println(fileContent);
- js三级联动下拉框
3213213333332132
三级联动
//三级联动
省/直辖市<select id="province"></select>
市/省直辖<select id="city"></select>
县/区 <select id="area"></select>
- erlang之parse_transform编译选项的应用
616050468
parse_transform游戏服务器属性同步abstract_code
最近使用erlang重构了游戏服务器的所有代码,之前看过C++/lua写的服务器引擎代码,引擎实现了玩家属性自动同步给前端和增量更新玩家数据到数据库的功能,这也是现在很多游戏服务器的优化方向,在引擎层面去解决数据同步和数据持久化,数据发生变化了业务层不需要关心怎么去同步给前端。由于游戏过程中玩家每个业务中玩家数据更改的量其实是很少
- JAVA JSON的解析
darkranger
java
// {
// “Total”:“条数”,
// Code: 1,
//
// “PaymentItems”:[
// {
// “PaymentItemID”:”支款单ID”,
// “PaymentCode”:”支款单编号”,
// “PaymentTime”:”支款日期”,
// ”ContractNo”:”合同号”,
//
- POJ-1273-Drainage Ditches
aijuans
ACM_POJ
POJ-1273-Drainage Ditches
http://poj.org/problem?id=1273
基本的最大流,按LRJ的白书写的
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
#define INF 0x7fffffff
int ma
- 工作流Activiti5表的命名及含义
atongyeye
工作流Activiti
activiti5 - http://activiti.org/designer/update在线插件安装
activiti5一共23张表
Activiti的表都以ACT_开头。 第二部分是表示表的用途的两个字母标识。 用途也和服务的API对应。
ACT_RE_*: 'RE'表示repository。 这个前缀的表包含了流程定义和流程静态资源 (图片,规则,等等)。
A
- android的广播机制和广播的简单使用
百合不是茶
android广播机制广播的注册
Android广播机制简介 在Android中,有一些操作完成以后,会发送广播,比如说发出一条短信,或打出一个电话,如果某个程序接收了这个广播,就会做相应的处理。这个广播跟我们传统意义中的电台广播有些相似之处。之所以叫做广播,就是因为它只负责“说”而不管你“听不听”,也就是不管你接收方如何处理。另外,广播可以被不只一个应用程序所接收,当然也可能不被任何应
- Spring事务传播行为详解
bijian1013
javaspring事务传播行为
在service类前加上@Transactional,声明这个service所有方法需要事务管理。每一个业务方法开始时都会打开一个事务。
Spring默认情况下会对运行期例外(RunTimeException)进行事务回滚。这
- eidtplus operate
征客丶
eidtplus
开启列模式: Alt+C 鼠标选择 OR Alt+鼠标左键拖动
列模式替换或复制内容(多行):
右键-->格式-->填充所选内容-->选择相应操作
OR
Ctrl+Shift+V(复制多行数据,必须行数一致)
-------------------------------------------------------
- 【Kafka一】Kafka入门
bit1129
kafka
这篇文章来自Spark集成Kafka(http://bit1129.iteye.com/blog/2174765),这里把它单独取出来,作为Kafka的入门吧
下载Kafka
http://mirror.bit.edu.cn/apache/kafka/0.8.1.1/kafka_2.10-0.8.1.1.tgz
2.10表示Scala的版本,而0.8.1.1表示Kafka
- Spring 事务实现机制
BlueSkator
spring代理事务
Spring是以代理的方式实现对事务的管理。我们在Action中所使用的Service对象,其实是代理对象的实例,并不是我们所写的Service对象实例。既然是两个不同的对象,那为什么我们在Action中可以象使用Service对象一样的使用代理对象呢?为了说明问题,假设有个Service类叫AService,它的Spring事务代理类为AProxyService,AService实现了一个接口
- bootstrap源码学习与示例:bootstrap-dropdown(转帖)
BreakingBad
bootstrapdropdown
bootstrap-dropdown组件是个烂东西,我读后的整体感觉。
一个下拉开菜单的设计:
<ul class="nav pull-right">
<li id="fat-menu" class="dropdown">
- 读《研磨设计模式》-代码笔记-中介者模式-Mediator
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/*
* 中介者模式(Mediator):用一个中介对象来封装一系列的对象交互。
* 中介者使各对象不需要显式地相互引用,从而使其耦合松散,而且可以独立地改变它们之间的交互。
*
* 在我看来,Mediator模式是把多个对象(
- 常用代码记录
chenjunt3
UIExcelJ#
1、单据设置某行或某字段不能修改
//i是行号,"cash"是字段名称
getBillCardPanelWrapper().getBillCardPanel().getBillModel().setCellEditable(i, "cash", false);
//取得单据表体所有项用以上语句做循环就能设置整行了
getBillC
- 搜索引擎与工作流引擎
comsci
算法工作搜索引擎网络应用
最近在公司做和搜索有关的工作,(只是简单的应用开源工具集成到自己的产品中)工作流系统的进一步设计暂时放在一边了,偶然看到谷歌的研究员吴军写的数学之美系列中的搜索引擎与图论这篇文章中的介绍,我发现这样一个关系(仅仅是猜想)
-----搜索引擎和流程引擎的基础--都是图论,至少像在我在JWFD中引擎算法中用到的是自定义的广度优先
- oracle Health Monitor
daizj
oracleHealth Monitor
About Health Monitor
Beginning with Release 11g, Oracle Database includes a framework called Health Monitor for running diagnostic checks on the database.
About Health Monitor Checks
Health M
- JSON字符串转换为对象
dieslrae
javajson
作为前言,首先是要吐槽一下公司的脑残编译部署方式,web和core分开部署本来没什么问题,但是这丫居然不把json的包作为基础包而作为web的包,导致了core端不能使用,而且我们的core是可以当web来用的(不要在意这些细节),所以在core中处理json串就是个问题.没办法,跟编译那帮人也扯不清楚,只有自己写json的解析了.
- C语言学习八结构体,综合应用,学生管理系统
dcj3sjt126com
C语言
实现功能的代码:
# include <stdio.h>
# include <malloc.h>
struct Student
{
int age;
float score;
char name[100];
};
int main(void)
{
int len;
struct Student * pArr;
int i,
- vagrant学习笔记
dcj3sjt126com
vagrant
想了解多主机是如何定义和使用的, 所以又学习了一遍vagrant
1. vagrant virtualbox 下载安装
https://www.vagrantup.com/downloads.html
https://www.virtualbox.org/wiki/Downloads
查看安装在命令行输入vagrant
2.
- 14.性能优化-优化-软件配置优化
frank1234
软件配置性能优化
1.Tomcat线程池
修改tomcat的server.xml文件:
<Connector port="8080" protocol="HTTP/1.1" connectionTimeout="20000" redirectPort="8443" maxThreads="1200" m
- 一个不错的shell 脚本教程 入门级
HarborChung
linuxshell
一个不错的shell 脚本教程 入门级
建立一个脚本 Linux中有好多中不同的shell,但是通常我们使用bash (bourne again shell) 进行shell编程,因为bash是免费的并且很容易使用。所以在本文中笔者所提供的脚本都是使用bash(但是在大多数情况下,这些脚本同样可以在 bash的大姐,bourne shell中运行)。 如同其他语言一样
- Spring4新特性——核心容器的其他改进
jinnianshilongnian
spring动态代理spring4依赖注入
Spring4新特性——泛型限定式依赖注入
Spring4新特性——核心容器的其他改进
Spring4新特性——Web开发的增强
Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC
Spring4新特性——Groovy Bean定义DSL
Spring4新特性——更好的Java泛型操作API
Spring4新
- Linux设置tomcat开机启动
liuxingguome
tomcatlinux开机自启动
执行命令sudo gedit /etc/init.d/tomcat6
然后把以下英文部分复制过去。(注意第一句#!/bin/sh如果不写,就不是一个shell文件。然后将对应的jdk和tomcat换成你自己的目录就行了。
#!/bin/bash
#
# /etc/rc.d/init.d/tomcat
# init script for tomcat precesses
- 第13章 Ajax进阶(下)
onestopweb
Ajax
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- Troubleshooting Crystal Reports off BW
blueoxygen
BO
http://wiki.sdn.sap.com/wiki/display/BOBJ/Troubleshooting+Crystal+Reports+off+BW#TroubleshootingCrystalReportsoffBW-TracingBOE
Quite useful, especially this part:
SAP BW connectivity
For t
- Java开发熟手该当心的11个错误
tomcat_oracle
javajvm多线程单元测试
#1、不在属性文件或XML文件中外化配置属性。比如,没有把批处理使用的线程数设置成可在属性文件中配置。你的批处理程序无论在DEV环境中,还是UAT(用户验收
测试)环境中,都可以顺畅无阻地运行,但是一旦部署在PROD 上,把它作为多线程程序处理更大的数据集时,就会抛出IOException,原因可能是JDBC驱动版本不同,也可能是#2中讨论的问题。如果线程数目 可以在属性文件中配置,那么使它成为
- 正则表达式大全
yang852220741
html编程正则表达式
今天向大家分享正则表达式大全,它可以大提高你的工作效率
正则表达式也可以被当作是一门语言,当你学习一门新的编程语言的时候,他们是一个小的子语言。初看时觉得它没有任何的意义,但是很多时候,你不得不阅读一些教程,或文章来理解这些简单的描述模式。
一、校验数字的表达式
数字:^[0-9]*$
n位的数字:^\d{n}$
至少n位的数字:^\d{n,}$
m-n位的数字:^\d{m,n}$
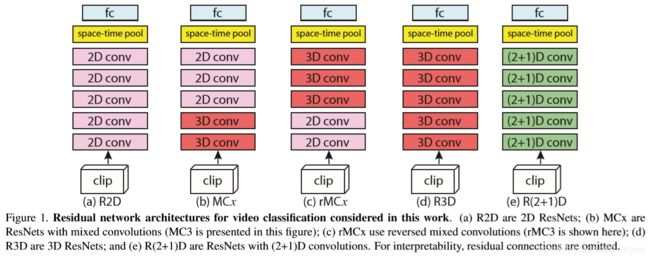

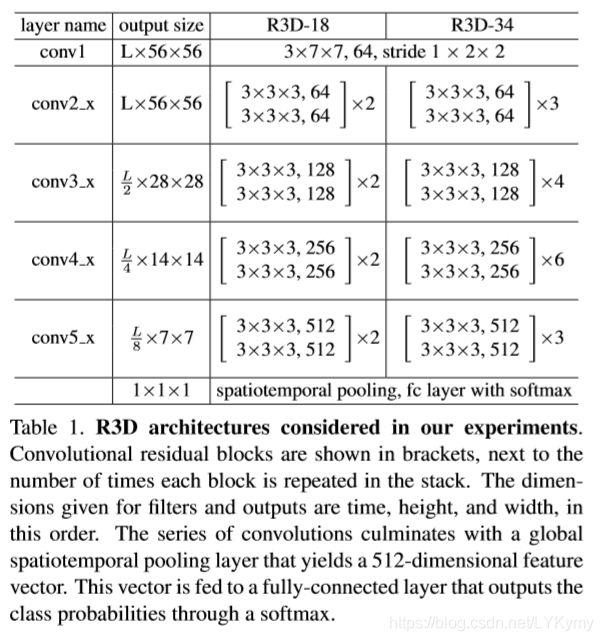

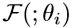 实现了由权重θi参数化的两个卷积的合成以及ReLU函数的应用。 在这项工作中,我们考虑网络,其中卷积残差块的序列最终达到顶层,在整个时空量上执行全局平均池化,并负责最终分类预测。
实现了由权重θi参数化的两个卷积的合成以及ReLU函数的应用。 在这项工作中,我们考虑网络,其中卷积残差块的序列最终达到顶层,在整个时空量上执行全局平均池化,并负责最终分类预测。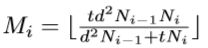 ,以便(2 + 1)D块中的参数数量大约等于实现完整3D卷积的参数数量。 我们注意到,这种时空分解可以应用于任何3D卷积层。 图2给出了简化设置的分解示意图,其中输入张量zi-1包含单个通道(即Ni-1 = 1)。 如果3D卷积具有空间或时间跨度(执行降采样),则该跨度将相应地分解为其空间或时间维度。 图1(e)中说明了这种架构。
,以便(2 + 1)D块中的参数数量大约等于实现完整3D卷积的参数数量。 我们注意到,这种时空分解可以应用于任何3D卷积层。 图2给出了简化设置的分解示意图,其中输入张量zi-1包含单个通道(即Ni-1 = 1)。 如果3D卷积具有空间或时间跨度(执行降采样),则该跨度将相应地分解为其空间或时间维度。 图1(e)中说明了这种架构。