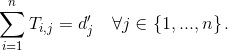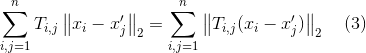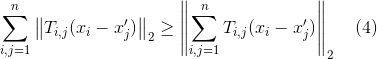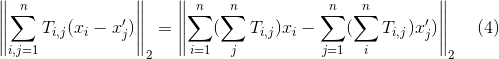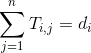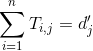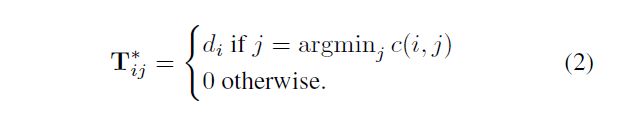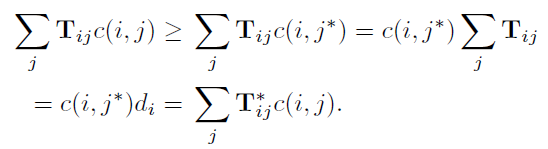From Word Embeddings To Document Distances - Review

前言：

本博文是对论文From Word Embeddings To Document Distances(Matt, Yu, Nicholas, Kilian, 2015)的一个问题， 第一部分是关于Abstract和第一小节的介绍内容。本文第二部分则是对原文第二部分和第三部分的一个简单总结，主要是介绍了一下对于文档分类技术的一个简单的源起和word2vec怎样运用到这个任务当中。本文第三部分，则会讨论算法的核心部分，也对应原文的第四部分。最后本文会概括性的介绍一下该模型的实验结果，总结还有一些个人的看法见解。

——————————————————————————————————————————————————

一、文章简介

这篇文章的基本思想在abstract已经完全说明了，就是运用在文档聚类技术上面的一个算法。首先引入词向量的值，然后就能在一个高维嵌入空间里面去计算两个单词的距离。由于word2vec之类的词向量技术的出现，使得我们能够用向量距离来表达两个词的相似度。于是本文作者就提出，如果我们能计算出两个文档之间词语的距离之和，那我们就能够用这个距离来估算相似性。这就是文中Word Mover's Distance(WMD) metric的由来，这种metric基于Earth Mover's Distance（EMD）metric。另外一个值得注意的是，这个模型没有超参数调节，这也使得其模型表现更为稳定，并为训练省却了很多麻烦。

接下来作者阐述了一些文档分类/聚类和相似度检测的基本原理。要能够测量文档的相似度，毫无疑问我们首先要找到办法表达文档。在传统的NLP中，两个可以使用的文档分类方法一个是bag of words（BOW），也就是简单的one-hot向量，在这种情况下虽然作者在此处未说明，但是最传统的对比方式毫无疑问就是列温斯顿距离。另一种较为传统的方法就是运用TF-IDF表示。这两种表达的问题都在于过于稀疏，以及经常会出现的特征空间的“近正交”（near orthogonality）问题。 这种表达还有一个短处就是，没办法衡量词与词之间的距离，这导致明明两句很相似的两句话在表达上则可能差距很大。一个例子就是”奥巴马在伊利诺伊州对媒体发表讲话"和”总统在芝加哥会见了各大传媒”（注：本文发表的2015年，奥巴马仍然是时任美国总统；另，芝加哥是伊利诺伊州的城市）。这两句话尽管每一个单词都不一样，但是表达的意思却几近相同。但是，由于单词选择的不同，在传统的表达方式里面，这两个词的特征空间几乎是正交的，换句话说，机器很可能判定他们是完全不同的两句话。这里插一句话，虽然作者在这里探讨的是文档分类和表达的问题。但是这个例子其实更靠近的是NLP里面另外一个非常经典的NLP任务，那就是共指消解问题。这个问题的定义就是，如何将两个指代同一个具体对象但文字表达却不同的词组词汇联系在一起。虽然运用词向量在很大程度上缓解了这个问题，但是我觉得却不是万能的。另外共指消解问题，在构建知识图谱抽取上也有着一定的作用。不过由于这里作者是在用这个例子来阐明两个文本之间的差距，而不是同一个文本之中，前后段落的指代问题。所以词向量以及足够去解决这个问题了。

作者接下来介绍了一些现有的用来解决刚才所说的特征正交问题的传统机器学习模型。 比如隐藏语义分析（LSI）和Latent Dirichlet Allocation（LDA）这类传统的文本主体统计模型。前者运用了矩阵的SVD分解来得出文本的主体模型。后者则是利用了贝叶斯学派的思想和迪莉切特模型来对文本向量进行分析。两者都在文本主题识别上有着不错的表现，都能够得出一个文本的主题分布模型。后文作者也会以这两个经典统计模型作为标杆来对比自己提出的算法的效果。作者接下来也引出了自己提出的新模型的思想，为了方便介绍，我会把这一段介绍放到本文的第二个部分来介绍。

二、相关工作，word2vec以及模型的基础思想

作者在第二部分简单介绍了一些早期的相关工作，并且引出了早期一些尝试使用EMD和LSI算法对比文本的工作。然后也介绍了一下EMD问题现有的研究，并且提到之前的相关研究的一个问题是在高维度特征计算上效率不高无法用GPU假设。所以作者重新设计了EMD的metric并提出了本文的主旨WMD。紧接着，原文的第三部分作者提到了著名的word2vec文本表达。并简单阐述了模型的基础原理，在这里作者距离的是skip-gram的word2vec，也就是根据一个词窗口选定中心词去最大化近邻词的后验概率的模型。并且特别强调了训练之后的词向量表达具有的距离特征。比如两个词如果十分类似，则它们的向量夹角距离会很小，以及对词语关系的向量表达。比如，v(爱因斯坦） - v（科学家） + v（毕加索）  v（画家）这样的关系在word2vec里面是存在的。

最后，让我们在此基础上再把WMD的基础思想过一遍。首先作者指出，这一距离的意义是建立在word2vec词向量表达所提供的特性上的。如同我之前提出的那些性质一样，如果两个单词直接能通过向量之间的距离来表达语义的差距，那么我们自然能够把文本之间相似度问题转化为其内部词向量的差距问题。进一步的，作者提出，如果我们把词向量代入到文本的词汇当中，并且赋予一个权重值，那么我们可以计算两个文档之间的一个距离值WMD。这个WMD是两个文档之间，所有单词A到所有单词B之间的最短距离和。而对WMD距离的优化则是要用到EMD问题的方法。 这个WMD距离的三个优点在于：第一是完全没有任何超参数需要调节；第二是它有很强的可解读性；第三就是有着不错的召回率。下一部分就让我们从细节入手来解读这篇论文的核心部分。

三、论文核心算法解读

在介绍算法之前，我们先申明和规定一些符号表达。首先我们假设我们的word2vec词嵌入空间表达是,其中n是词汇量，d则是表达空间的维度。换句话说，X就是一个巨大的词向量矩阵代表了所有的词汇。值得注意的是，这个矩阵的每一列代表一个单词的d维向量。我们假设用一个经过归一化处理的BOW模型去表达所有的文档，每一个单词i，如果在文档中出现了词，则我们用表达这个词的权重。一个文档向量我们表达为d（是的，我也觉得这么表达非常容易混淆），其中每一个维度i就是我们刚才说的一个词的权重表达，当然这种表达是稀疏的，因为大部分词都不会出现在某一个文档。

nBOW 表达： 这里作者又再次解释了一下BOW表达是什么，我就不再赘述了，具体可以回看本文第一部分的介绍。

Word travel cost： 然后作者引出了Word travel cost，并且用 来表达两个单词i，j之间的距离。注意，这里的距离计算实际上就类似于计算两个向量点的欧氏距离，并没有什么特殊的。

Document distance：接下来就是对文档距离的计算了，首先我们规定两个nBOW表达的文档向量d和d'，并且我们规定任何一个d中的单词都能够转变成d'中任意的一个单词，换句话说，我们不限定两个文档里的单词之间的映射关系。并且，我们用一个稀疏的浮点矩阵来表达两个文档之间单词变换的关系。这个矩阵中的每一个单元 代表的就是一个文档d中的单词i转换到文档d'中单词j的数量。这个地方要进行说明一下，大家应该还记得，在一个经过normalization处理后的nBOW表达的文档向量d中，每一个单词都有一个权重。这个值是该单词的出现频率归一化之后得来的。所以我们可以认为也代表了文档中某个单词i出现的次数。那么如果我们已知文档d中的某个词i出现了两次，但是这两次有分别应该对应文档d'中的单词j和k，那么i和j，k的映射值就分别为1(未进行归一化前）。从这里也能看出，其实这个距离最关键的地方在于，能够把两个文档之中相似的词对应起来的能力。当然，由于outgoing和incoming的映射关系应该守恒的原理，我们可以得出以及。我们可以这样来理解这两个公式，第一个公式里面等号左侧的意义就是对于某个文档d的单词i，我们将它所有和文档d'中的不同单词j的映射值加起来，应该等于其本身在文档d中出现的次数。比如我之前举的例子，的值就为2（未经归一化处理）。在理解这一点之后，我们就能把两个文档的距离表达为。这个表达其实也不难理解，就是把两个文档之间所有映射的权重和这些对应单词i，j之间的word travel cost取内积的结果。

Transportation problem：在上述的介绍之后，我们不难把对文档距离的优化问题写成以下形式：

                                   

Subject to:    

                    

到这里不难看出，我们原有的问题被转化成了一个线性规划的优化问题。这里的两个约束条件，其实就是我们之前介绍的两个outgoing和incoming映射守恒的条件。而这个问题也已经是一个早就被研究过的transportation problem，也是EMD的一个特例。

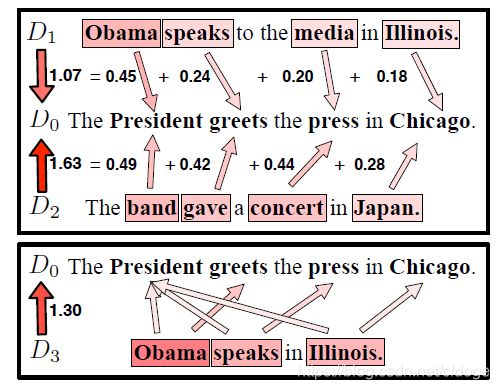
作者还在这里放了一张图来解释这个距离的原理：

从上图的例子我们可以一窥WMD的原理。在上半部分的例子里面，假设我们给定三个短文本，. 其中和相似度很高而和语义相似度很低。然后我们可以看到，通过WMD的优化，我们可以把语义最接近的两个词拿来计算距离。比如里的Obama和中的总统一次就有很低的距离，而中的乐队和中的总统一次的距离就是0.49，高于Obama的距离。而同样的，伊利诺伊和芝加哥的语义距离也比日本和芝加哥的语义距离小很多。

WMD的原理和算法我们就介绍完了，接下来作者又对计算WMD的算法进行了效率优化。作者首先指出当前的优化方式的复杂度是, 其中p代表一篇文档的词汇量大小，这一复杂度如果运用在较大的文档上无疑是太慢了。于是作者提出了三个优化方法。

word centroid distance：第一种优化方法是首先计算质心（centroid）距离，并且用该距离来作为WMD的lower bound进行过滤。我们可以用一个简单的数学过程证明这一个方案的可行性。

    我们把等号右半部分定位（2）式， 并通过变换得到（3）式如下：

并且，由于二次模函数是一个凸函数，我们能够运用Jason inequality（詹森不等式）性质如下：

对于凸函数f(x), .

这里，我们将看作凸函数f(x), 同时把加总函数看作g(x)就可以运用上述性质变换式（3）并得到不等式（4）如下：

而不等号右边的部分又能够做一个简单的变换得到等式（5)如下:

 

这一步的变换只是简单的运用了乘法分配律的性质而已。但是如果还记得之前我们提到的两个约束条件的话就不难实际上式子里的

，   于是我们可以变换式（4）右半边得到式（5）

 

而式（5）的右半边就正好等于我们之前要求的质心距离，我们将这个距离称作WCD，而不难看出这个计算复杂度线性于文档和词汇数量的O(dp)。得到的这个WCD现在就可以作为一个下确界使用，用以过滤调重复的计算。比如说，在进行k聚类算法的时候，我们先计算每一个文档的WCD值,这时候我们只花费了线性时间。而再从这些文档中，选取WCD值最小的前k或者前2k个文本和中心文本进行WMD比对，这样可以大大节省时间。

Relaxed word moving distance （RWMD）： 虽然我们证明了WCD是一个线性复杂度的WMD的下确界，但是作者认为，WCD还不够逼近WMD，于是打算使用一个更紧的下确界来进一步过滤计算。作者使用的方法是，放松两个限制条件中的一个，将原优化问题改成如下的问题：

Subject to:    

作者指出，这个放松之后的优化问题得到的最优解必然是原问题的一个lower bound，因为不管原问题怎样针对第二个条件进行优化，他都是建立在第一个优化条件的最优解集里面的。就找到最短距离的时候，假设找到了一个点为最优，另一个点不管怎么变换都是建立在第一个点固定的情况下。（想象挂一幅画，钉好了第一颗钉子对齐第二颗钉子的感觉）

这时我们可以将这个新的优化问题的最优解写成以下形式：

并且证明如下：

并且当我们移除一个限制条件以后，从d到d’的距离和反过来基本相同。于是我们把两个距离写作，，，并且我们尝试去寻找两个中比较大的一个作为最逼近的那个下确界，这种下确界的总体计算复杂度是

Prefetch and prune：最后一个技巧则是算法上通过结合两种不同的下确界WCD和RWMD来得到最优的速度和结果。作者再次以k聚类问题为例，我们首先还是使用WCD距离来对所有候选文档进行排序，随后选择其中k个WCD最小的候选文档。然后以第k个最小的WCD文档的RWMD值作为阈值，计算刚才筛选的k个文档以外的剩下的文档的RWMD值，并和阈值进行比对。大于阈值的文档，我们就直接不考虑了，否则就进行WMD的计算来最终确定它的距离。由于RWMD非常的逼近于WMD，所以在好的情况下，可以过滤95%的候选文档，节省了大量的时间。

四、结果与总结

本文的第五部分对这个WMD算法和经典的文档表达和分类算法进行了比对，分别在八个文档分类数据集上通过knn聚类来比对其效果。在比对当中，对文本进行去停词，和去低频词的基本清洗操作。结果是，WMD聚类在六个问题上做到了最好的效果（见下图），紧随其后的则是LSI，隐藏语义分析算法，而在bbcsport文档分类问题上WMD也败给了LSI分类的表现。

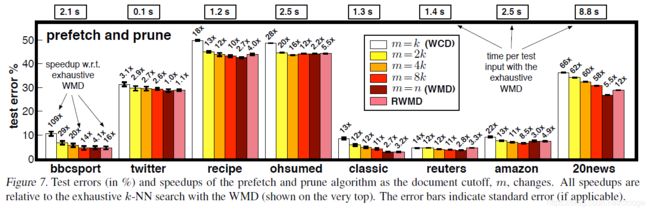
作者也对如何使用WCD和RWMD来过滤计算进行了实验（见下图），下图中每个条状图代表的是只计算通过WCD筛选出来的m个候选文本进行RWMD比对再计算WMD的优化算法的错误率，条状图上面的数字代表该方法几倍快于只使用WMD进行计算的时间。从图中不难看出，尽管通过WCD选取前k个候选文本的速度非常快，但是由于WCD的宽松性，使得准确度有所下降。当我们扩大WCD选取文本的数量为2k-8k个的时候，错误率就逐步下降。

个人总结：

在读完这篇文章后，个人对于怎样运用无监督预训练的词向量方面又有了新的理解。之前也有接触过一些通过使用word2vec的预训练向量来完成文本分类的任务。在不深度网络架构的前提下，一些模型对于词向量的处理都过于粗略，要么是直接把一句话的每个词语加权平均得出一个值，要么就是通过人为设定一些特征来使用词向量。这些方法个人觉得并没有能很好地利用到词与词之间的距离关系，尤其是简单的加总，对于短文本尚且可能有效，对于较长的文本就基本很难起效了，甚至不如一些不使用词向量的主题模型的效果。这篇文章虽然看似自然语言问题，词向量运用问题，但其实本质上是一个算法优化问题，线性规划问题。这种当时看来非常精妙的通过计算一个最小加总词向量距离的算法，确实是为解决文本分类提供了一个非深度网络的方法。

另外值得注意的一个地方是，这个算法还简介通过优化提供了一个文本对齐的副产品。在前神经网络时代的机器翻译里面，单词对齐的问题往往要通过一个后验概率模型来进行对齐。但这个分类通过最优化不同的词向量之间的距离，间接的为我们提供了这样一个对齐的功能，不知道这个思路能不能也运用在机器翻译上面呢。

最后，在优化部分，作者也使用两个不同下确界，一个较松但是运算容易，一个较紧但运算成本较高，来进行候选文本筛选。并且也是先通过较松但是计算容易的下确界来进行广泛的筛选，最终确定一个较小的范围。再通过较紧的下确界来筛选可能遗漏的文本，并最终通过成本最高的原本计算来进行最终筛选。这让我想起了前一篇读过的论文，Searching and Mining Trillions of Time Series Subsequences under Dynamic Time Warping （hanawin Rakthanmanon， 2012）里面的cascading lower bound算法。也是通过逐层使用由松到紧下确界来过滤重复计算的技巧。可见这种优化算法是可以推广到任意复杂计算的算法上的，只要满足以下两个条件：1.你能找到计算复杂度更低下确界（这几乎总是能找到），2.你能找到计算复杂度稍低的下确界，但却是相对逼近于真实值。

以上，就是我对本篇论文的一些粗浅理解。