强化学习策略梯度梳理2 - AC(附代码)
策略梯度梳理 AC
- Actor-Critic
- Actor-Critic Policy Gradient (QAC)
- QAC with shared network
- one-step AC
- AC( λ \lambda λ)
主要参考文献 Reinforcement Learning: An introduction,Sutton
主要参考课程 Intro to Reinforcement Learning,Bolei Zhou
相关文中代码 https://github.com/ThousandOfWind/RL-basic-alg.git
Actor-Critic
Actor-Critic Policy Gradient (QAC)
从REINFORCE到AC主要就是把MC的估计方式换成自举。
可以把REINFORCE里的 G t G_t Gt 替换为critic: Q ( S t , A t , w ) Q(S_t, A_t, \boldsymbol{w}) Q(St,At,w)
∇ J ( θ ) ∝ E π [ Q ( S t , A t , w ) ∇ ln ( π ( A t ∣ S t , θ ) ) ] \nabla J(\boldsymbol{\theta}) \propto \mathbb{E}_{\pi}\left[Q(S_t, A_t, \boldsymbol{w})\nabla \operatorname{ln}(\pi(A_t \mid S_t, \boldsymbol{\theta}))\right] ∇J(θ)∝Eπ[Q(St,At,w)∇ln(π(At∣St,θ))]
这个Q可以简单的用TD更新
def get_action(self, observation, *arg):
obs = th.FloatTensor(observation)
pi = self.pi(obs=obs)
m = Categorical(pi)
action_index = m.sample()
self.log_pi_batch.append(m.log_prob(action_index))
self.value_batch.append(self.Q(obs=obs)[action_index])
return int(action_index), pi
def learn(self, memory):
batch = memory.get_last_trajectory()
reward = th.FloatTensor(batch['reward'][0])
log_pi = th.stack(self.log_pi_batch)
value = th.stack(self.value_batch)
mask = th.ones_like(value)
mask[-1] = 0
next_value = th.cat([value[1:], value[0:1]],dim=-1) * mask
td_error = reward + self.gamma * next_value.detach() - value
td_loss = (td_error ** 2).mean()
J = - (value.detach() * log_pi).mean()
loss = J + td_loss
self.writer.add_scalar('Loss/J', J.item(), self._episode)
self.writer.add_scalar('Loss/TD_loss', td_loss.item(), self._episode)
self.writer.add_scalar('Loss/loss', loss.item(), self._episode)
self.optimiser.zero_grad()
loss.backward()
grad_norm = th.nn.utils.clip_grad_norm_(self.params, 10)
self.optimiser.step()
self._episode += 1
QAC with shared network
这个理论其实很简单,只是是共享actor网络和critic网络的特征提取层
但是常常担心会发生耦合而同流合污
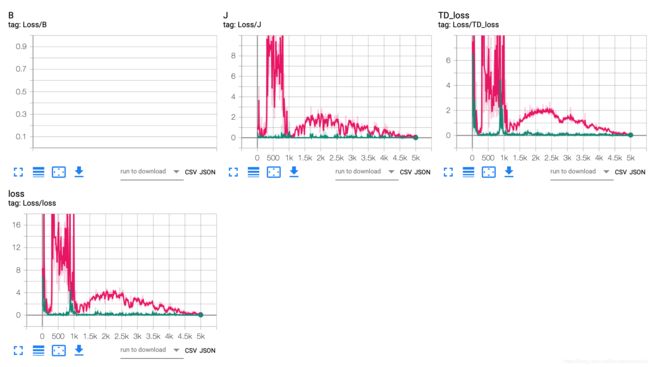
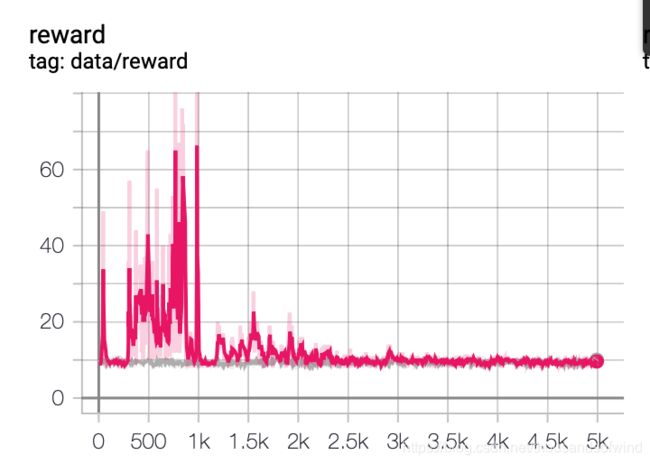
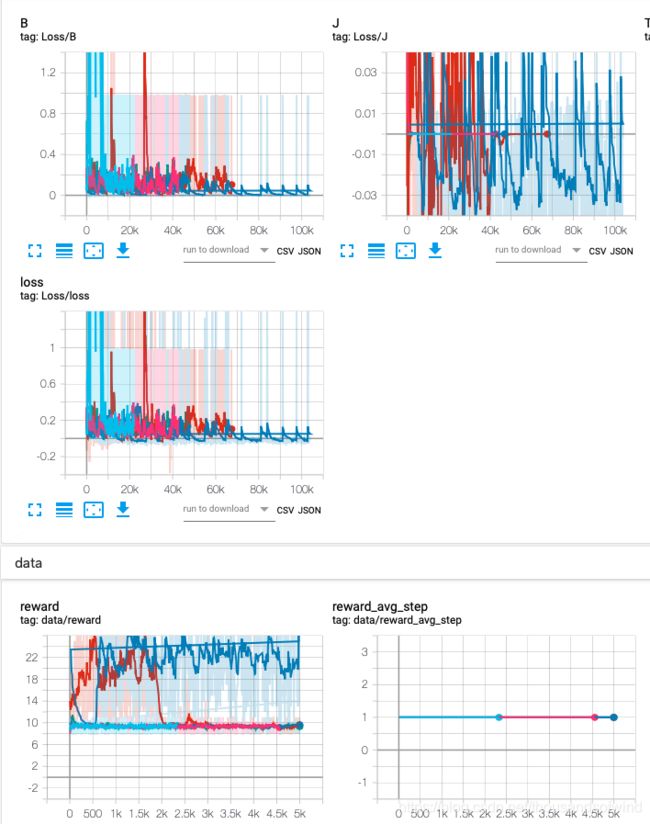
这结果烂着烂着我都习惯了
one-step AC
由于在REINFORCE-baseline中已经在用
∇ J ( θ ) ∝ E π [ ( G ( S t , A t ) − v ( S t ) ) ∇ ln ( π ( A t ∣ S t , θ ) ) ] \nabla J(\boldsymbol{\theta}) \propto \mathbb{E}_{\pi}\left[\left(G(S_{t},A_t) -v(S_t)\right)\nabla \operatorname{ln}(\pi(A_t \mid S_t, \boldsymbol{\theta}))\right] ∇J(θ)∝Eπ[(G(St,At)−v(St))∇ln(π(At∣St,θ))]
很自然的就可以
∇ J ( θ ) ∝ E π [ ( R ( S t , A t ) + γ v ( S t + 1 ) − v ( S t ) ) ∇ ln ( π ( A t ∣ S t , θ ) ) ] \nabla J(\boldsymbol{\theta}) \propto \mathbb{E}_{\pi}\left[\left(R(S_{t},A_t) + \gamma v(S_{t+1}) -v(S_t)\right)\nabla \operatorname{ln}(\pi(A_t \mid S_t, \boldsymbol{\theta}))\right] ∇J(θ)∝Eπ[(R(St,At)+γv(St+1)−v(St))∇ln(π(At∣St,θ))]
这样我们就有了one step AC算法

def get_action(self, observation, *arg):
obs = th.FloatTensor(observation)
pi = self.pi(obs=obs)
m = Categorical(pi)
action_index = m.sample()
self.log_pi = m.log_prob(action_index)
return int(action_index), pi
def learn(self, memory):
batch = memory.get_last_trajectory()
obs = th.FloatTensor(batch['observation'])
next_obs = th.FloatTensor(batch['next_obs'])
value = self.V(obs).squeeze(0)
next_value = self.V(next_obs).squeeze()
td_error = batch['reward'][0] + batch['done'][0] * self.gamma * next_value.detach() - value
J = - ((self.I * td_error).detach() * self.log_pi)
value_loss = (td_error ** 2)
loss = J + value_loss
self.I *= self.gamma
self.writer.add_scalar('Loss/J', J.item(), self._episode)
self.writer.add_scalar('Loss/B', value_loss.item(), self._episode)
self.writer.add_scalar('Loss/loss', loss.item(), self._episode)
self.optimiser.zero_grad()
loss.backward()
grad_norm = th.nn.utils.clip_grad_norm_(self.pi.parameters(), 10)
grad_norm = th.nn.utils.clip_grad_norm_(self.V.parameters(), 10)
self.optimiser.step()
self._episode += 1
为什么J-loss会出现负数还是没没整明白这个理论上看式子应该始终是正才对忘了这里引入了baseline, 那自然会有正有负没毛病
Sutton 书里是这样的,但我不是很明白为什么 I I I 被用在 θ \theta θ的更新中,。后面的资格迹也是我从前没有涉及过的领域,等我看完前章再来复现吧