竞赛(一)kaggle mercari
比赛的数据可以在下节中的竞赛官网链接中下到,且本文提供了完整的训练代码,可以供大家练手。
题目详解
简单理解就是通过输入的用户以及物品特征来预测物品的真实价格,原始题目提供了如下有趣的例子:
It can be hard to know how much something’s really worth. Small details can mean big differences in pricing. For example, one of these sweaters cost $335 and the other cost $9.99. Can you guess which one’s which?
解题思路
出于了解深度学习和tensorflow的想法,这里参考了下ololo大神的tensorflow-starter方法,虽然代码格式写的有些凌乱,但是思路很清晰,命名很清晰明了。
数据分析
由于不知道如何在kernel上进行代码的编写和结果的提交,因而只能在本地搞一搞,大致将数据按照7(train):2(validation):1(test)的方式划分开,数据样例如下所示:
可以看出数据总共有7列:name、item_condition_id、category_name、brand_name、price、shipping、item_description,其中price列是label,其他都是特征列,简单观察之后发现name、category_name、brand_name、item_description这些列都是英文组成,item_condition_id和shipping都是数值特征,因而一个简单的想法是将第一类特征用embedding的方式转换为数字特征,将第二类特征通过one-hot的方式转换为编码特征,之后将所有处理后的特征拼接在一起进行后续的学习任务。
整体思路
ololo大神的做法和我想的完全不同,他的主要思想是针对每一维特征进行特征处理,之后进行卷积处理,最后将卷积处理后的数据拼接在一起,后面拼接上两个全连接层得到最终的price预测结果。如下是针对每一维特征的处理和学习过程的示意图。
-
name
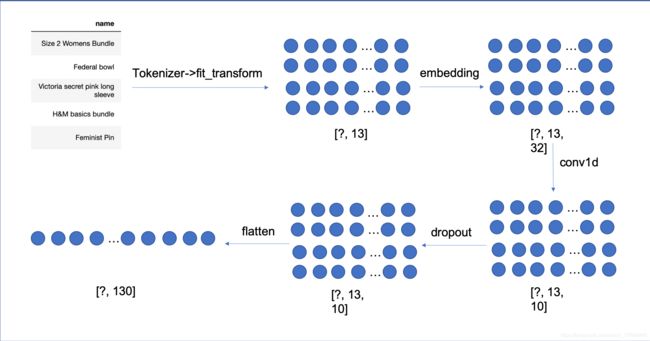
操作流程如下所示,这里附了一份粗略的流程图:- 通过Tokenizer类将name中的每个单词都处理成一个词表中的索引值
- 创建单词的embedding向量,向量维度为32维
- 对数据进行一维卷积,一维卷积的解释可以见这里
- dropout处理
- flatten处理,最终产出维度为130维的特征向量
-
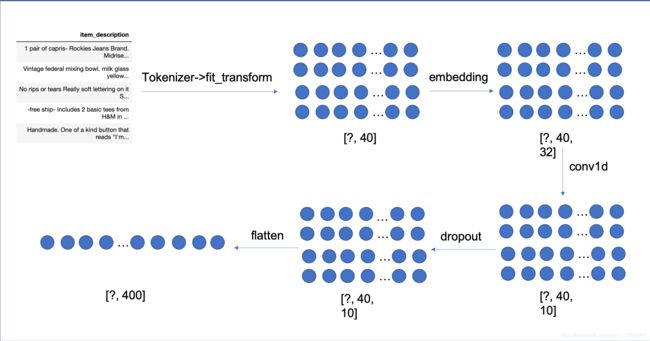
item_description
description的处理手段和name类似,这里就不再赘述,直接贴图: -
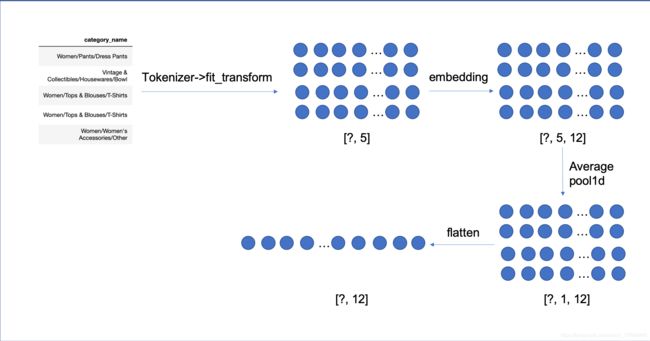
category_name
category_name的处理手段和上述两维特征的处理手段有所不同,因为category_name的每一个样例并不是单纯的句子,而是由"/"组成的类目树,因而这里采用了一个特殊的处理手段,即将类目信息直接展开,例如类目信息为 a/b/c, 输出 [a, a/b, a/b/c],再将这三个元素分别用词表索引+embedding+conv1d的方式进行学习,思路如下所示: -
brand_name
brand_name相对简单,因而不需要通过卷积的方式来进行学习,直接embedding+flatten解决问题。 -
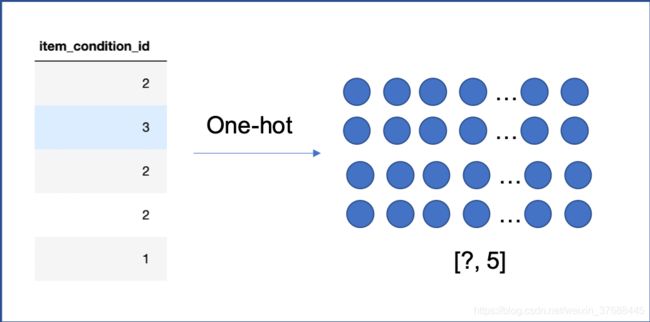
item_condition_id
这里我和大神的想法一致,都是直接采用one-hot编码 -
shipping
由于这维特征只有0和1,这里已经是one-hot编码了,因而不需要对其进行额外的操作。 -
concat
将上述所有的数据concat到一起,之后拼接全链接层,得到最终结果。
代码
ololo大神原先模型训练的核心代码如下所示:
graph = tf.Graph()
graph.seed = 1
with graph.as_default():
place_name = tf.placeholder(tf.int32, shape=(None, name_seq_len))
place_desc = tf.placeholder(tf.int32, shape=(None, desc_seq_len))
place_brand = tf.placeholder(tf.int32, shape=(None, 1))
place_cat = tf.placeholder(tf.int32, shape=(None, cat_seq_len))
place_ship = tf.placeholder(tf.float32, shape=(None, 1))
place_cond = tf.placeholder(tf.uint8, shape=(None, 1))
place_y = tf.placeholder(dtype=tf.float32, shape=(None, 1))
place_lr = tf.placeholder(tf.float32, shape=(), )
# title
name = embed(place_name, name_voc_size, name_embeddings_dim)
name = conv1d(name, num_filters=10, filter_size=3)
name = tf.nn.dropout(name, keep_prob=0.5)
name = tf.layers.flatten(name)
tf.summary.histogram("name", name)
print("name.shape is {}".format(name.shape))
# description
desc = embed(place_desc, desc_voc_size, desc_embeddings_dim)
desc = conv1d(desc, num_filters=10, filter_size=3)
desc = tf.nn.dropout(desc, keep_prob=0.5)
desc = tf.layers.flatten(desc)
tf.summary.histogram("desc", desc)
print("desc.shape is {}".format(desc.shape))
# brand
brand = embed(place_brand, brand_voc_size, brand_embeddings_dim)
brand = tf.layers.flatten(brand)
tf.summary.histogram("brand", brand)
print("brand.shape is {}".format(brand.shape))
# category
cat = embed(place_cat, cat_voc_size, cat_embeddings_dim)
cat = tf.layers.average_pooling1d(cat, pool_size=cat_seq_len, strides=1, padding='valid')
cat = tf.layers.flatten(cat)
tf.summary.histogram("cat", cat)
print("cat.shape is {}".format(cat.shape))
# ship
ship = place_ship
# condition
cond = tf.one_hot(place_cond, 5)
cond = tf.layers.flatten(cond)
out = tf.concat([name, desc, brand, cat, ship, cond], axis=1)
print('concatenated dim:', out.shape)
out = dense(out, size=100, activation=None)
out = tf.nn.dropout(out, keep_prob=0.5)
out = dense(out, size=1)
loss = tf.losses.mean_squared_error(place_y, out)
tf.summary.scalar("loss", loss)
rmse = tf.sqrt(loss)
train_step = tf.train.AdamOptimizer(learning_rate=place_lr).minimize(loss)
init = tf.global_variables_initializer()
merged = tf.summary.merge_all() # merge_all需要在graph的定义中声明,否则无效
经过41400次迭代基本收敛,最后几次validation的loss如下所示:
iter: 40200, loss: 0.4161092936992645
iter: 40500, loss: 0.4169567823410034
iter: 40800, loss: 0.4157225489616394
iter: 41100, loss: 0.4162442088127136
iter: 41400, loss: 0.41495734453201294
而我这里对他的模型做了下改进,将最后的全链接层用FM模型替代,这样做的目的是为了更好地学习到特征之间的关系,FM模型的详解可以见这里,改进代码如下:
w_0 = tf.Variable(tf.random_normal([1], stddev=0.01))
W = tf.Variable(tf.random_normal([out.shape[1].value, 1], stddev=0.01))
linear_out = tf.add(tf.matmul(out, W), w_0)
k = 5
V = tf.Variable(tf.random_normal([out.shape[1].value, k], stddev=0.01))
complex_output = tf.multiply(tf.reduce_sum(tf.subtract(tf.pow(tf.matmul(out, V), 2), \
tf.matmul(tf.pow(out, 2), tf.pow(V, 2))), \
axis=1, keep_dims=True), 0.5)
out_y = tf.add(linear_out, complex_output)
lambda_w = tf.constant(0.001, dtype=tf.float32)
lambda_v = tf.constant(0.001, dtype=tf.float32)
regularization = tf.reduce_sum(tf.multiply(lambda_w, tf.pow(W, 2))) + \
tf.reduce_sum(tf.multiply(lambda_v, tf.pow(V, 2)))
loss = tf.losses.mean_squared_error(place_y, out_y) + regularization
tf.summary.scalar("loss", loss)
通过改进之后,同样经过41400次迭代基本收敛,最后几次validation的loss如下所示:
iter: 40200, loss: 0.39779549837112427
iter: 40500, loss: 0.3979751765727997
iter: 40800, loss: 0.3977966904640198
iter: 41100, loss: 0.39837953448295593
iter: 41400, loss: 0.39793896675109863
可以发现性能确实得到很大的改善。
参考
- 代码网址
- mercari竞赛官网
- 参考解题思路