图论算法——最短路径算法

引言

在Prim算法和Kruskal算法中，我们学习了寻找加权无向图的最小生成树的Prim算法：构造最小生成树的每一步都向生成树中添加一条新的边。

今天要学习类似的方法来计算最短路径——Dijkstra算法。

Dijkstra算法

最短路径树中的边：edgeTo[v]的值为树中连接v和它的父节点的边。

最短路径树：包含了顶点s到所有可达的顶点的最短路径

distTo[v]表示从s到v的已知最短路径的长度

Dijkstra算法构造最小生成树的每一步都向生成树中添加一条新的边。首先将distTo[s]初始化为0，distTo[]中的
其他元素初始化为正无穷。然后将distTo[]最小的非树顶点加入树中，如此，知道所有的顶点都在树中。

下面通过实例图解分析一下该算法。

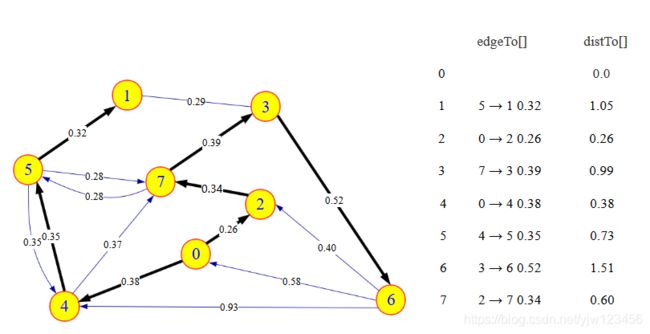
对上篇文章图论算法——加权有向图的数据结构中的图例求解最短路径树，过程如下：

初始将0加入优先队列，然后将0增加到最短路径树，同时让它出队。它的邻接点2和4加入到优先队列中。从队列中找到distTo[]值最小的为distTo[2]=0.26，将对应的边0→2加粗标红。

从队列中删除顶点2，将0→2添加到树中，将7加入优先队列。此时distTo[7] = 0.26 + 0.34 = 0.60。图中黑色粗线表示该条边已经在树中，如0→2。

从队列中删除顶点4，将0→4添加到树中，将5加入优先队列。这里没有将7加入优先队列是因为当前distTo[7] = 0.60 小于从0->4,4->7的路径权重和，意味着边4->7失效。

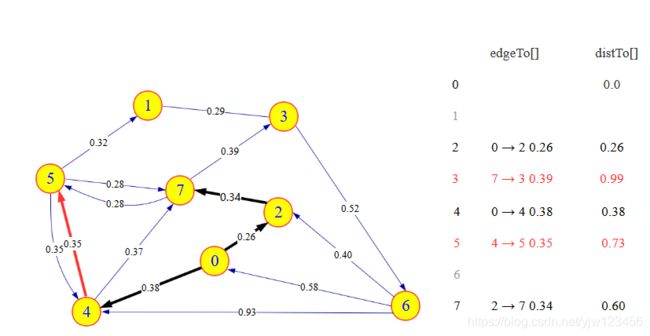
从队列中删除顶点7，将2→7添加到树中，将3加入优先队列。边7->5失效。

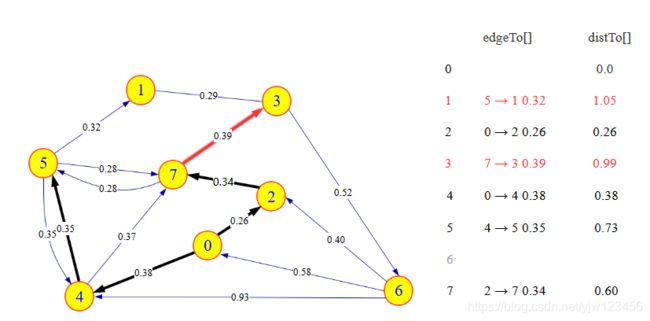
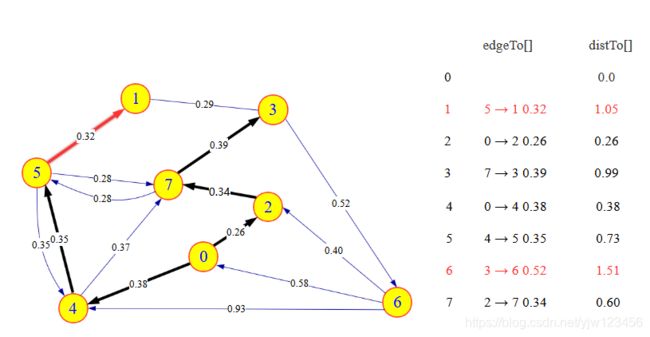
从队列中删除顶点5，将4→5添加到树中，将1加入优先队列。边5->7失效。

从队列中删除顶点3，将7→3添加到树中，将6加入优先队列。

从队列中删除顶点1，将5→1添加到树中，边1->3失效。

从队列中删除顶点6，将3→6添加到树中。

代码

package com.algorithms.graph;

import com.algorithms.heap.IndexMinPQ;
import com.algorithms.stack.Stack;

/**
 * 最短路径算法
 * @author yjw
 * @date 2019/6/6/006
 */
public class DijkstraSP {
    /**
     * edgeTo[v]表示从s到v的最短路径上的最后一条边
     */
    private DirectedEdge[] edgeTo;
    /**
     * distTo[v]为从s到v的已知最短路径的长度
     */
    private double[] distTo;
    private IndexMinPQ<Double> pq;

    public DijkstraSP(EdgeWeightedDigraph g, int s) {
        edgeTo = new DirectedEdge[g.vertexNum()];
        distTo = new double[g.vertexNum()];
        pq = new IndexMinPQ<>(g.vertexNum());

        //初始化
        for (int v = 0; v < g.vertexNum(); v++) {
            distTo[v] = Double.POSITIVE_INFINITY;
        }
        //将起点到自己的距离声明为0
        distTo[s] = 0.0;
        //入队
        pq.insert(s, 0.0);

        while (!pq.isEmpty()) {
            visit(g, pq.deleteMin());
        }
    }

    private void visit(EdgeWeightedDigraph g, int v) {
        for (DirectedEdge e : g.adj(v)) {
            int w = e.to();
            //distTo[w] > distTo[v] + e.weight()
            //意思就是，如果经由v点到w点，权重比之前更小（路径更短）,则选择经由v点
            if (Double.compare(distTo[w], distTo[v] + e.weight()) > 0) {
                //更新从s到w的最短路径长度
                distTo[w] = distTo[v] + e.weight();
                //更新边
                edgeTo[w] = e;

                //pq中是否含有w
                if (pq.contains(w)) {
                    //更新索引w对应的值，可能会调整索引堆的结构
                    pq.changeKey(w, distTo[w]);
                } else {
                    //不存在则插入pq
                    pq.insert(w, distTo[w]);
                }
            }
        }
    }

    public double distTo(int v) {
        return distTo[v];
    }

    public boolean hasPathTo(int v) {
        return distTo[v] < Double.POSITIVE_INFINITY;
    }

    public Iterable<DirectedEdge> pathTo(int v) {
        if (!hasPathTo(v)) {
            return null;
        }
        Stack<DirectedEdge> path = new Stack<>();
        //从终点开始，不断的取上一条路径,因此利用了栈来打印成起点到终点的正序
        for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
            path.push(e);
        }
        return path;
    }

    public static void main(String[] args) {
        EdgeWeightedDigraph g = new EdgeWeightedDigraph(8);
        g.addEdges(0,2,.26,4,.38);
        g.addEdge(1,3,.29);
        g.addEdge(2,7,.34);
        g.addEdge(3,6,.52);
        g.addEdges(4,7,.37,5,.35);
        g.addEdges(5,1,.32,7,.28,4,.35);
        g.addEdges(6,4,.93,0,.58,2,.40);
        g.addEdges(7,3,.39,5,.28);

        DijkstraSP dsp = new DijkstraSP(g,0);

        for (int v = 0; v < g.vertexNum(); v++) {
            if (dsp.hasPathTo(v)) {
                System.out.print("0 to " + v + ": ");
                for (DirectedEdge e : dsp.pathTo(v)) {
                    System.out.print(e +" ");
                }
                System.out.println();
            }
        }
    }
}

其中用到的IndexMinPQ见图解索引二叉堆

在一幅含有V个顶点和E条边的加权有向图中，使用Dijkstra算法计算根节点为给定起点的最短路径树所需的空间与V成正比，时间与ElogV成正比(最坏情况下)