P5905 【模板】Johnson 全源最短路 题解

博客园同步

原题链接

前置知识：

$\text{dijkstra}$ 模板

简要题意：

求任意两点的最短路。图中可能有 负环，负权，重边，自环 等现象。

显然我们先建图。

算法一

对于 $20\%$ 的数据，$1\le n\le 100$，不存在负环（可用于验证 $\text{Floyd}$ 正确性）

嗯，出题人都告诉你用 $\text{Floyd}$ 了，而且 $\text{Floyd}$ 的代码简洁得出奇，所以这 $20pts$ 完全是送给你啦！

时间复杂度：$O(n^3)$.

实际得分：$20pts$.

算法二

对于另外 $20\%$ 的数据，$w\ge 0$（可用于验证 $\text{Dijkstra}$ 正确性）

出题人真善良，算法都告诉你了。

$\text{Dijkstra}$ 跑 $n$ 次，然后队列优化（不优化肯定连部分分都拿不到了）

时间复杂度：$O(nm\log n)$.

实际得分：$40pts$.（结合前面的 $\text{Floyd}$）

算法三

我们基于 $\text{Dijkstra}$ 的思路思考，因为这个思路不会超时，我们需要想一个办法解决 负环 问题。

可以想到的一种办法，把所有边权加上一个值使得不存在负权，然后再减回去。但是 理想是美好的，现实是残酷的 这样贪心完全错了。

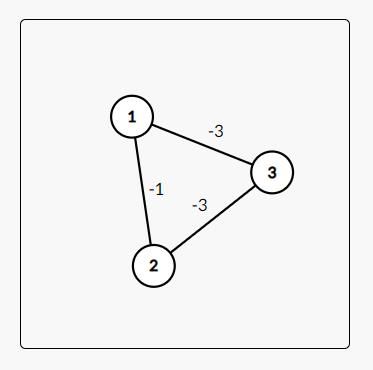
比方说：

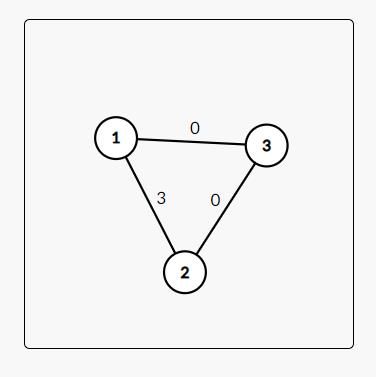
你先把每条边 $+3$ 变成：

求出最短路为 $0$. 然而正确的答案是 $-4$，你怎么减也减不出这个值。其错误在于，假设走了多条边的最短路与另一条走了较少边的次短路，加上值之后最短路就不一定还是最短路了。

这样要是能解决我们还要 $\text{Johnson}$ 干么

他提出了一种思想，解决这种问题：

• 构造一个“上帝节点” $0$ 号，并且建边 $(0,i,0)(1\le i\le n)$.（即向每个点建一条权值为 $0$ 的边）

• 用 $\text{SPFA}$ 一遍求出 $h_i$ 表示 $0$ 号节点到 $i$ 号节点的最短路（顺便可以判负环）。

• 此时如果有一条 $u\to v$ 权值为 $w$ 的边，则 $w\leftarrow w+h_u-h_v$.

• 这时对图跑 $n$ 轮 $\text{dijkstra}$ 即可得到答案。

首先，我们了解这个算法的基本过程后，来研究一个问题：

为什么 $w\leftarrow w+h_u-h_v$ 是正确的呢？

显然原图是有向图，那么其实这个操作就把 每条最短路都减去了一个对应的数值，具体从 $s$ 到 $t$ 最短路的例子：

重构后的图，最短路形如：

$$s\to a_1(w_{s,a_1}+h_s-h_{a_1})\to a_2(w_{a_1,a_2}+h_{a_1}-h_{a_2})\to \cdots \to a_n\to t(w_{a_n,t}+h_{a_n}-h_t)$$

$$=s\to a_1(w_{s,a_1})\to a_2(w_{a_1,a_2})+\cdots \to a_n\to t(w_{a_n,t})+h_s-h_t$$

这真是太秒了！其实最短路只是在原来的最短路上加上了一个 $h_s-h_t$，我们把这玩意儿最后减掉就行了。

所以，最终我们用 $\text{SPFA}$ 和 $\text{dijkstra}$ 一起通过了本题。

时间复杂度：$O(nm\log n+nm)=O(nm\log n)$.

（这个数在 $n=3\times 10^3,m=6\times 10^3$ 的时候会达到 $2\times 10^8$，请注意 常数优化）

实际得分：$100pts$.

#pragma GCC optimize(2)
#include
using namespace std;

#define INF 1e9
const int N=5e3+1;
typedef long long ll;

inline int read(){char ch=getchar();int f=1;while(ch<'0' || ch>'9') {if(ch=='-') f=-f; ch=getchar();}
	int x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}

struct node {
	int dis,id;
	inline bool operator < (const node &x) const {
		return dis>x.dis;
	} node (int x,int y) {dis=x,id=y;}
} ; bool vis[N];
int n,m,in[N];
ll h[N],dis[N];
vector<pair<int,int> > G[N];

inline bool SPFA(int s) { //从源点开始求一遍最短路 , 记为 h
	queue<int>q; memset(h,0x3f,sizeof(h));
	h[s]=0; vis[s]=1; q.push(s);
	while(!q.empty()) {
		int u=q.front(); q.pop(); vis[u]=0;
		for(int i=0;i<G[u].size();i++) {
			int v=G[u][i].first,w=G[u][i].second;
			if(h[v]>h[u]+w) {
				h[v]=h[u]+w;
				if(!vis[v]) {
					vis[v]=1; q.push(v);
					if(++in[v]>=n) return 0;
				}
			}
		}
	} return 1;
}

inline void dijkstra(int s) { //从每个点开始走一遍最短路模板
	priority_queue<node> q; memset(vis,0,sizeof(vis));
	for(int i=1;i<=n;i++) dis[i]=(i==s)?0:(INF);
	q.push(node(0,s)); while(!q.empty()) {
		int u=q.top().id; q.pop(); if(vis[u]) continue;
		vis[u]=1; for(int i=0;i<G[u].size();i++) {
			int v=G[u][i].first,w=G[u][i].second;
			if(dis[v]>dis[u]+w) {
				dis[v]=dis[u]+w;
				if(!vis[v]) q.push(node(dis[v],v));
			}
		}
	}
}

int main(){
	n=read(),m=read();
	while(m--) {
		int u=read(),v=read(),w=read();
		G[u].push_back(make_pair(v,w));
//		G[v].push_back(make_pair(u,w));
	} for(int i=1;i<=n;i++) G[0].push_back(make_pair(i,0)); //创造上帝视角
	if(!SPFA(0)) {puts("-1");return 0;} //负环结束
	for(int u=1;u<=n;u++)
	for(int i=0;i<G[u].size();i++) 
		G[u][i].second+=h[u]-h[G[u][i].first]; //重构
	for(int i=1;i<=n;i++) {
		dijkstra(i); ll ans=0;
		for(int j=1;j<=n;j++)
			ans+=(dis[j]==INF)?(j*INF):(j*(dis[j]+h[j]-h[i]));
		printf("%lld\n",ans);	//跑最短路并统计答案
	}	
	return 0;
}