粒子滤波

%在二维空间,假设运动物体的一组(非线性)运动位置、速度、加速度数据,用粒子滤波方法进行处理

%实验室的博客

 

% 参数设置
N = 100;   %粒子总数
Q = 5;      %过程噪声
R = 5;      %测量噪声
T = 10;     %测量时间
theta = pi/T;       %旋转角度
distance = 80/T;    %每次走的距离
WorldSize = 100;    %世界大小
X = zeros(2, T);    %存储系统状态
Z = zeros(2, T);    %存储系统的观测状态
P = zeros(2, N);    %建立粒子群
PCenter = zeros(2, T);  %所有粒子的中心位置
w = zeros(N, 1);         %每个粒子的权重
err = zeros(1,T);     %误差
X(:, 1) = [50; 20];     %初始系统状态
Z(:, 1) = [50; 20] + wgn(2, 1, 10*log10(R));    %初始系统的观测状态

 

%初始化粒子群
for i = 1 : N
    P(:, i) = [WorldSize*rand; WorldSize*rand];
    dist = norm(P(:, i)-Z(:, 1));     %与测量位置相差的距离
    w(i) = (1 / sqrt(R) / sqrt(2 * pi)) * exp(-(dist)^2 / 2 / R);   %求权重
end

PCenter(:, 1) = sum(P, 2) / N;      %所有粒子的几何中心位置

 

%%

err(1) = norm(X(:, 1) - PCenter(:, 1));     %粒子几何中心与系统真实状态的误差

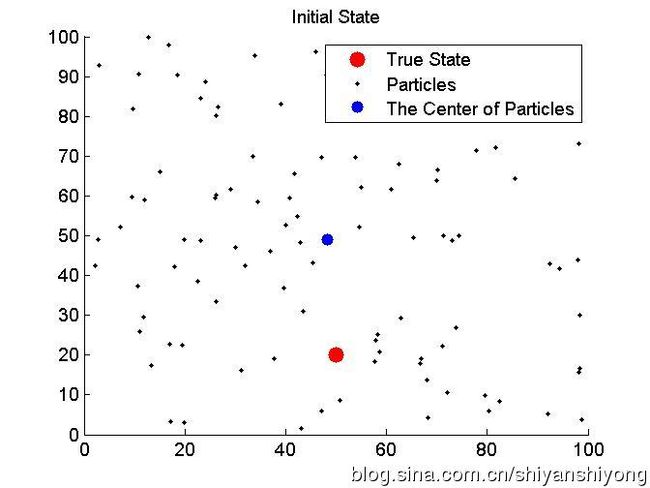
figure(1);
set(gca,'FontSize',12);
hold on
plot(X(1, 1), X(2, 1), 'r.', 'markersize',30)   %系统状态位置
axis([0 100 0 100]);
plot(P(1, :), P(2, :), 'k.', 'markersize',5);   %各个粒子位置
plot(PCenter(1, 1), PCenter(2, 1), 'b.', 'markersize',25); %所有粒子的中心位置
legend('True State', 'Particles', 'The Center of Particles');
title('Initial State');
hold off

%%

%开始运动
for k = 2 : T
       
    %模拟一个弧线运动的状态
    X(:, k) = X(:, k-1) + distance * [(-cos(k * theta)); sin(k * theta)] + wgn(2, 1, 10*log10(Q));     %状态方程
    Z(:, k) = X(:, k) + wgn(2, 1, 10*log10(R));     %观测方程 
   
    %粒子滤波
    %预测
    for i = 1 : N
        P(:, i) = P(:, i) + distance * [-cos(k * theta); sin(k * theta)] + wgn(2, 1, 10*log10(Q));
        dist = norm(P(:, i)-Z(:, k));     %与测量位置相差的距离
        w(i) = (1 / sqrt(R) / sqrt(2 * pi)) * exp(-(dist)^2 / 2 / R);   %求权重
    end

    %归一化权重
    wsum = sum(w);
    for i = 1 : N
        w(i) = w(i) / wsum;
    end
   
    %重采样（更新）
    for i = 1 : N
        wmax = 2 * max(w) * rand;  %另一种重采样规则
        index = randi(N, 1);
        while(wmax > w(index))
            wmax = wmax - w(index);
            index = index + 1;
            if index > N
                index = 1;
            end          
        end
        P(:, i) = P(:, index);     %得到新粒子
    end
   
    PCenter(:, k) = sum(P, 2) / N;      %所有粒子的中心位置
   
    %计算误差
    err(k) = norm(X(:, k) - PCenter(:, k));     %粒子几何中心与系统真实状态的误差
   
    figure(2);
    set(gca,'FontSize',12);
    clf;
    hold on
    plot(X(1, k), X(2, k), 'r.', 'markersize',50);  %系统状态位置
    axis([0 100 0 100]);
    plot(P(1, :), P(2, :), 'k.', 'markersize',5);   %各个粒子位置
    plot(PCenter(1, k), PCenter(2, k), 'b.', 'markersize',25); %所有粒子的中心位置
    legend('True State', 'Particle', 'The Center of Particles');
    hold off
    pause(0.1);
end

 

%%

figure(3);
set(gca,'FontSize',12);
plot(X(1,:), X(2,:), 'r', Z(1,:), Z(2,:), 'g', PCenter(1,:), PCenter(2,:), 'b-');
axis([0 100 0 100]);
legend('True State', 'Measurement', 'Particle Filter');
xlabel('x', 'FontSize', 20); ylabel('y', 'FontSize', 20);

%%

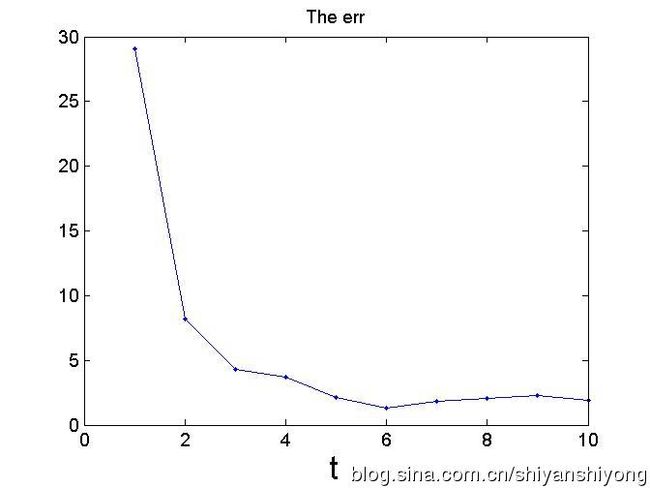
figure(4);
set(gca,'FontSize',12);
plot(err,'.-');
xlabel('t', 'FontSize', 20);
title('The err');