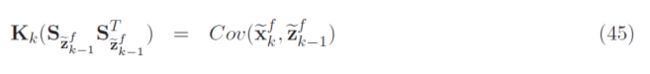[译]无迹卡尔曼滤波教程
无迹卡尔曼滤波器
https://www.cse.sc.edu/~terejanu/files/tutorialUKF.pdf
翻译的文件可以直接在这里下载:https://download.csdn.net/download/hmmwjs/12272357
翻译主要依靠 百度翻译
内容如下:
Unscented Kalman Filter Tutorial
无迹卡尔曼滤波教程
Gabriel A. Terejanu
Department of Computer Science and Engineering University at Buffalo, Buffalo, NY 14260 [email protected]
1 Introduction
1 介绍
The Unscented Kalman Filter belongs to a bigger class of filters called Sigma-Point Kalman Filters or Linear Regression Kalman Filters, which are using the statistical linearization technique [1, 5]. This technique is used to linearize a nonlinear function of a random variable through a linear regression between n points drawn from the prior distribution of the random variable. Since we are considering the spread of the random variable the technique tends to be more accurate than Taylor series linearization [7].
Unscented Kalman滤波器属于Sigma点Kalman滤波器或线性回归Kalman滤波器的一大类,它们使用统计线性化技术[1,5]。这项技术是用来线性化一个随机变量的非线性函数通过线性回归之间的n点从随机变量的先验分布。由于我们考虑的是随机变量的扩散,因此该技术往往比泰勒级数线性化更精确[7]。
In the same family of filters we have The Central Difference Kalman Filter, The Divided Differ- ence Filter, and also the Square-Root alternatives for UKF and CDKF [7].
在同一类滤波器中,我们有中心差分Kalman滤波器、分割差分滤波器以及UKF和CDKF的平方根备选方案[7]。
In EKF the state distribution is propagated analytically through the first-order linearization of the nonlinear system due to which, the posterior mean and covariance could be corrupted. The UKF, which is a derivative-free alternative to EKF, overcomes this problem by using a deterministic sam-pling approach [9]. The state distribution is represented using a minimal set of carefully chosen sample points, called sigma points. Like EKF, UKF consists of the same two steps: model forecast and data assimilation, except they are preceded now by another step for the selection of sigma points.
在EKF中,状态分布通过非线性系统的一阶线性化进行解析传播,从而破坏了后验均值和协方差。UKF是EKF的无导数替代品,它通过使用确定性抽样方法克服了这个问题[9]。状态分布用一组精心选择的样本点表示,称为sigma点。与EKF一样,UKF也包括同样的两个步骤:模型预测和数据同化,只是在这两个步骤之前还有另一个选择sigma点的步骤。
2 UKF Algorithm
2 无迹卡尔曼滤波器算法
The UKF is founded on the intuition that it is easier to approximate a probability distribution that it is to approximate an arbitrary nonlinear function or transformation [4]. The sigma points are chosen so that their mean and covariance to be exactly xa
and Pk−1. Each sigma point is then propagated through the nonlinearity yielding in the end a cloud of transformed points. The new estimated mean and covariance are then computed based on their statistics. This process is called unscented transfor- mation. The unscented transformation is a method for calculating the statistics of a random variable which undergoes a nonlinear transformation [9].
UKF建立在这样的直觉基础上:它更容易逼近概率分布,即它是逼近任意非线性函数或变换的[4]。选择sigma点,使其平均值和协方差恰好为(xa)和(Pk-1)。然后每个sigma点通过非线性传播,最后产生一个转换点云。新的估计平均值和协方差然后根据它们的统计数据计算。这个过程称为无迹变换。无迹变换是一种计算经过非线性变换的随机变量统计量的方法[9]。
Consider the following nonlinear system, described by the difference equation and the observation model with additive noise:
考虑以下非线性系统,由差分方程和含附加噪声的观测模型描述:
The initial state x0 is a random vector with known mean µ0 = E[x0] and covariance P0 = E[(x0 − µ0)(x0 − µ0)T ]. In the case of non-additive process and measurement noise, the unscented transformation scheme is applied to the augmented state [9]:
初始状态x0是具有已知平均值μ0=E[x0]和协方差p=E[(x0-μ0)(x0-μ0)T]的随机向量。在非加性过程和测量噪声的情况下,将无迹变换方案应用于增广状态[9]:
Set Selection of Sigma Points
设置sigma点的选择
Let Xk−1 be a set of 2n + 1 sigma points (where n is the dimension of the state space) and their associated weights:
设Xk-1是一组2n+1 sigma点(其中n是状态空间的维数)及其相关权重:
Consider the following selection of sigma points, selection that incorporates higher order information in the selected points [4]:
考虑以下sigma点的选择,即在所选点中包含高阶信息的选择[4]:
where the weights must obey the condition:
其中权重必须符合以下条件:
and ![]() is the row or column of the matrix square root of
is the row or column of the matrix square root of ![]() controls the
controls the
position of sigma points: W 0 ≥ 0 points tend to move further from the origin, W 0 ≤ 0 points tend to be closer to the origin. A more general selection scheme for sigma points, called 4, is given in [9, 2].
(![]() )是
)是![]() 的矩阵平方根的行或者列。W0 控制sigma点的位置:W 0≥0点倾向于离原点更远,w0≤0点倾向于离原点更近。在[9,2]中给出了一种更通用的sigma点选择方案,称为标度无迹变换。
的矩阵平方根的行或者列。W0 控制sigma点的位置:W 0≥0点倾向于离原点更远,w0≤0点倾向于离原点更近。在[9,2]中给出了一种更通用的sigma点选择方案,称为标度无迹变换。
Model Forecast Step
Each sigma point is propagated through the nonlinear process model:
每个sigma点通过非线性过程模型传播:
The transformed points are used to compute the mean and covariance of the forecast value of xk :
转换后的点用于计算xk预测值的均值和协方差:
We propagate then the sigma points through the nonlinear observation model:
我们通过非线性观测模型传播sigma点:
With the resulted transformed observations, their mean and covariance (innovation covariance) is computed:
根据转换后的观测结果,计算其平均值和协方差(创新协方差):
The cross covariance between ![]() is:
is:
Data Assimilation Step
数据同化步骤
We like to combine the information obtained in the forecast step with the new observation measured
zk . Like in KF assume that the estimate has the following form:
我们喜欢将在预测步骤中获得的信息与新的观测测量zk相结合。就像在KF中一样,假设估算具有以下形式:
The gain Kk is given by:
增益Kk由下式给出:
The posterior covariance is updated after the following formula:
后验协方差在下列公式之后更新:
3 Square-Root UKF
平方根UKF
Note that in order to compute the new set of sigma points we need the square root matrix of the pos- terior covariance each time (Pk = Sk ST ). Since the update is applied to the full posterior covariance we can change the algorithm to propagate directly the square root matrix, Sk .
注意,为了计算新的sigma点集,我们每次都需要后验协方差的平方根矩阵(Pk=Sk ST)。由于更新应用于完全后验协方差,我们可以改变算法,直接传播平方根矩阵Sk。
The selection scheme of sigma points becomes:
sigma点的选择方案为:
The filter is initialized by computing the initial square root matrix via a Cholesky factorization of the full error covariance matrix.
滤波器通过对全误差协方差矩阵的Cholesky分解计算初始平方根矩阵来初始化。
Since W j > 0 for all i ≥ 1, in the time update step the forecast covariance matrix can be written as:
由于所有i≥1的W j>0,在时间更新步骤中,预测协方差矩阵可以写成:
Where ![]() is the square-root matrix of the process noise covariance matrix. This form is computationally undesirable since we have tripled the number of columns.
is the square-root matrix of the process noise covariance matrix. This form is computationally undesirable since we have tripled the number of columns.
其中![]() 是过程噪声协方差矩阵的平方根矩阵。这种形式在计算上是不可取的,因为我们已经将列数增加了三倍。
是过程噪声协方差矩阵的平方根矩阵。这种形式在计算上是不可取的,因为我们已经将列数增加了三倍。
We can use the QR-decomposition to express the transpose of the above matrix in terms of an orthogonal matrix ![]() and an upper triangular matrix
and an upper triangular matrix ![]() .
.
利用QR分解,我们可以用正交矩阵![]() 和上三角矩阵
和上三角矩阵![]() 来表示上述矩阵的转置。
来表示上述矩阵的转置。
Hence the error covariance matrix:
因此误差协方差矩阵:
In order to include the effect of the last term in the square-root matrix, we have to perform a rank 1 update to Cholesky factorization.
为了在平方根矩阵中包含最后一项的影响,我们必须对Cholesky分解执行秩1更新。
where sgn is the sign function and cholupdate returns the Cholesky factor of
其中sgn是符号函数,cholupdate返回
Therefore the forecast covariance matrix can be written![]() . The same way the posterior covariance can be expressed as
. The same way the posterior covariance can be expressed as ![]() and the innovation covariance as
and the innovation covariance as ![]() .
.
因此,预测协方差矩阵可以写成![]() ,后验协方差可以写成
,后验协方差可以写成![]() ,创新协方差可以写成
,创新协方差可以写成![]() 。
。
Time-update summary
时间更新摘要
Redraw sigma points to incorporate effect of process noise:
重新绘制sigma点,以纳入过程噪声的影响:
Propagate the new sigma points through measurement model:
通过测量模型传播新的sigma点:
The qr function returns only the lower triangular matrix.
qr函数只返回下三角矩阵。
Measurement-update summary
测量更新摘要
where / denotes a back-substitution operation. This is a better alternative to the matrix inversion. Since the Cholesky factor is a lower triangular matrix, we can find Kk using two back-substitution operations in the equation:
其中/表示反替换操作。这是矩阵求逆的一个更好的选择。由于Cholesky因子是一个下三角矩阵,我们可以在方程中使用两个反代换运算来求Kk:
In eqn. (44) since the middle argument of the cholupdate function is a matrix ∈ n×n
n consecutive updates of the Cholesky factor using the n columns of the matrix.
在公式(44)中,由于cholupdate函数的中间参数是一个![]() 的矩阵,结果是使用矩阵的n列对Cholesky因子进行n次连续更新。
的矩阵,结果是使用矩阵的n列对Cholesky因子进行n次连续更新。
Since QR-decomposition and Cholesky factorization tend to control better the round off errors and there are no matrix inversions, the SR-UKF has better numerical properties and it also guarantees positive semi-definiteness of the underlying state covariance [8].
由于QR分解和Cholesky分解倾向于更好地控制舍入误差,并且不存在矩阵逆,SR-UKF具有更好的数值特性,并且还保证了下垫状态协方差的正半确定性[8]。
4 Conclusion
The UKF represents the extra uncertainty on a linearized function due to linearization errors by the co-variance of the deviations between the nonlinear and the linearized function in the regression points [6].
UKF表示由于线性化误差导致的线性化函数的额外不确定性,由回归点中非线性函数和线性化函数之间的偏差的协方差表示[6]。
The approximations obtained with at least 2n + 1 sampling points are accurate to the 3rd order of Gaussian inputs for all nonlinearities and at least to the 2nd for non-Gaussian inputs. The Reduced Sigman Point Filters [3] uses only n + 1 sampling points but this time it does not take into account the linearization errors.
对于所有非线性,用至少2n+1个采样点获得的近似值精确到高斯输入的3阶,对于非高斯输入,至少精确到2阶。简化的Sigman点滤波器[3]仅使用n+1个采样点,但这次不考虑线性化误差。
References
- Arthur Gelb. Applied Optimal Estimation. M.I.T. Press, 1974.
[2] S. Julier. The Scaled Unscented Transformation, 1999.
[3] S. Julier, J. Jeffrey, and K. Uhlmann. Reduced Sigma Point Filters for the Propagation of Means and Covariances Through Nonlinear Transformations. 2002.
[4] S. J. Julier and J. K. Uhlmann. Unscented Filtering and Nonlinear Estimation. Proceedings of the IEEE, 92(3):401–422, 2004.
[5] Tine Lefebvre and Herman Bruyninckx. Kalman Filters for Nonlinear Systems: A Comparison of Performance.
[6] Tine Lefebvre and Herman Bruyninckx. Comment on ”A New Method for the Nonlinear Trans- formation of Means and Covariances in Filters and Estimators”. IEEE Trans.Automatic Control, 2002.
[7] R. van der Merwe. Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models. Technical report, 2003.
[8] R. van der Merwe and E. Wan. The Square-Root Unscented Kalman Filter for State and Parameter- Estimation, 2001.
[9] E. Wan and R. van der Merwe. The Unscented Kalman Filter. Wiley Publishing, 2001.


![[译]无迹卡尔曼滤波教程_第1张图片](http://img.e-com-net.com/image/info8/f37fd4954a2c44a49b4a8da38d5e20c1.jpg)


![[译]无迹卡尔曼滤波教程_第2张图片](http://img.e-com-net.com/image/info8/73e096310a8248fb888b51be56d5895b.jpg)

![[译]无迹卡尔曼滤波教程_第3张图片](http://img.e-com-net.com/image/info8/443d013bde1e4edaaa38d94dce41c8bd.jpg)


![[译]无迹卡尔曼滤波教程_第4张图片](http://img.e-com-net.com/image/info8/a198881b82a44ef092fed582ffc4cafb.jpg)
![[译]无迹卡尔曼滤波教程_第5张图片](http://img.e-com-net.com/image/info8/895e6cfbe3614113a4e47c901ae84bd5.jpg)



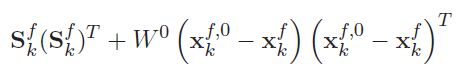
![[译]无迹卡尔曼滤波教程_第6张图片](http://img.e-com-net.com/image/info8/1ff8b9d44e0841779eaf16b4d62e0572.jpg)
![[译]无迹卡尔曼滤波教程_第7张图片](http://img.e-com-net.com/image/info8/56550527b0bb41f9b69c540845bb4f52.jpg)
![[译]无迹卡尔曼滤波教程_第8张图片](http://img.e-com-net.com/image/info8/090e0e0225604766aff2c2b6f719ab60.jpg)
![[译]无迹卡尔曼滤波教程_第9张图片](http://img.e-com-net.com/image/info8/5992a396796d49a58541d637b199d0e3.jpg)