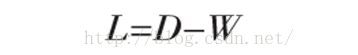谱聚类算法
一、什么是谱聚类算法
聚类的直观解释是根据样本间相似度,将它们分成不同组。谱聚类的思想是将样本看作顶点,样本间的相似度看作带权的边,从而将聚类问题转为图分割问题:找到一种图分割的方法使得连接不同组的边的权重尽可能低(这意味着组间相似度要尽可能低),组内的边的权重尽可能高(这意味着组内相似度要尽可能高)。根据相似度将这些顶点连起来,最后进行分割。分割后还连在一起的顶点就是同一类了。
谱聚类算法是数据挖掘中的一种聚类算法。
谱聚类算法是一种基于图论的算法:谱聚类算法将聚类问题转化为一个无向图的多路划分问题,数据点看成无向图G(V,E)中的顶点V,加权边的集合E={Sij}表示基于某一点相似性度量的两点间的相似度,用S表示待聚类数据点之间的相似性矩阵,图G中把聚类问题转变为在图G上的图划分问题,即将图G(V,E)划分为K个互不相交的子集V1,V2,...Vk,划分后每个子集Vi和Vj之间的相似程度较低,每个子集内部相似度较高。
记G=(V,E)表示一个无向加权图,V表示所有顶点的集合V={v1,...,vn},E表示所有边的集合,并且任意两点vi和vj的边具有非负权值wij≥0。图的邻接矩阵为W=(wij)i,j=1,...,n,如果wij=0则表示点vi和vj之间没有连接。由于G为无向图,所以其邻接矩阵具有对称性,即wij=wij。图中任一点vi的度为di=∑nj=1wij,表示一个点与其他所有点的连接情况,图的度矩阵D为每个点的度所构成的对角矩阵D=diag{d1,...,dn}。
二、谱聚类算法原理
谱聚类的思想就是要转化为图分割问题。因此,第一步就是将原问题转化为图。转为图有两个问题要解决:一是两个顶点的边要怎样定义;二是要保留哪些边。
对于第一个问题,如果两个点在一定程度上相似,就在两个点之间添加一条边。相似的程度由边的权重表示。因此,只要是计算相似度的公式都可用。要保留部分边的原因有:边太多了不好处理;权重太低的边是多余的。样本数据转化成图以后再求出样本无向完全图对应的矩阵,前面已经介绍了。接下来就是谱聚类中如何来处理矩阵模型(就是图的划分)。
提到图的划分下面我们就来介绍下谱聚类中用到的图的划分准则:谱聚类算法的思想来源于谱图划分,假定将每个数据样本看作图中的顶点V,根据样本间的相似度将顶点间的边E赋权重值W,这样就得到一个基于样本相似度的无项加权图G=(V,E)。那么在图G中就可将聚类问题转化为在图G上的图划分问题。
划分的要求:
子图内部相似度高,
图之间的相似度小。

图中一共有6个顶点,顶点之间的连线表示两个顶点的相似度,现在要将这图分成两半(两个类),要怎样分割(去掉哪边条)?根据谱聚类的思想,应该去掉的权值为0.1的边和0.2的边。最后,剩下的两半就分别对应两个类了。
聚类算法关键就是对图的划分,那怎么进行最优的划分?
一般有以下几种划分准则:
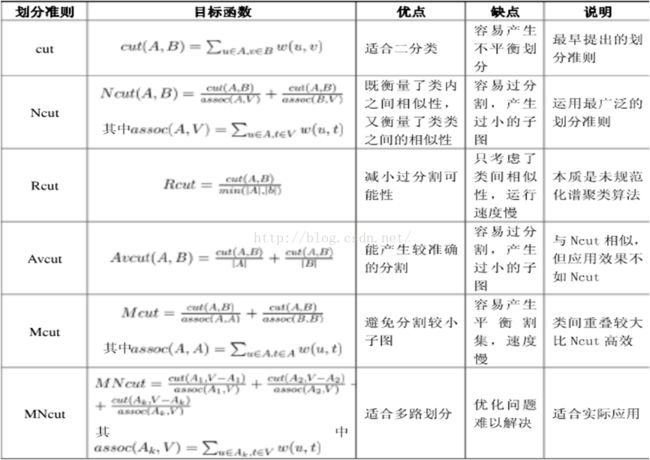
1、最小割集准则
2、规范割集准则
3、比例割集准则
4、平均割集准则
5、最小最大割集准则
6、多路规范割集准则有上面这六个划分准则,以最小割集为例老说明下划分原理:
如果我们想把一幅图像分割成K个子区域,那么我们可以通过递归调用最小割集的方法来实现,但是这个图像的分割方法有一个弊端;最小割集准则容易分割出图像中的孤立点集合。如下图所示:
最小割集准则: 谱图理论中,将图G划分为A,B两个子图。通过最小化上述剪切值来划分图G,这一划分准则被称为最小割集准则。用这个准则对一些图像进行分割,产生较好的效果,但是这个准则容易出现歪斜(即偏向小区域)分割。规范割集准则及比例割集准则均可避免这种情况的发生。
以下是几个划分准则的比较
划分准则有很多,那该怎样选取一个最优的划分?
对于图的划分就是要找到一个最优解,这样我们便可以将问题转化成求解相似矩阵或Laplacian矩阵的谱分解,谱聚类将图划分准则优化问题转换成求解相似矩阵或者Laplacian矩阵特征问题,可将此类方法统称为谱聚类方法,也可以认为谱聚类方法是对图划分准则的逼近。
三、谱聚类算法中的的数学模型
上面我们介绍了引入矩阵来辅助求解,转化成矩阵的模型后我们就要用到以下这些概
首先将对应的样本转化成完全图并存在矩阵中:
double sample[N][2]; //存放所有样本点(2维的)
void readSample(char *filename){
FILE *fp;
if((fp=fopen(filename,"r"))==NULL){
perror("fopen");
exit(0);
}
char buf[50]={0};
int i=0;
while(fgets(buf,sizeof(buf),fp)!=NULL){
char *w=strtok(buf," \t");
double x=atof(w);
w=strtok(NULL," \t");
double y=atof(w);
sample[i][0]=x;
sample[i][1]=y;
i++;
memset(buf,0x00,sizeof(buf));}
assert(i==N);
fclose(fp);
}念: 相似矩阵、度矩阵、 Laplacian 矩阵 。这里我们要讲到谱聚类中的关键内容——拉普拉斯矩阵,其定义为L=D–W,其中D和W就是上文定义的图的度矩阵和邻接矩阵。下面我们给出谱聚类中用到的拉普拉斯矩阵的一些性质。下面我们一上面的图为例来看看拉普拉斯矩阵。
拉普拉斯矩阵有两种形式:规范化的拉普拉斯矩阵和非规范化的拉普拉斯矩阵
1、非规范的拉普拉斯矩阵:
其中D为度矩阵,W为权值矩阵(对称的)
2、规范的拉普拉斯矩阵:
设有n个样本点X1,X2,...Xn,由某个相似函数(可以用计算欧式距离的公式)Sij=S(Xi,Xj),Sij非负,相似矩阵为S=(Sij)nxm
规范化谱聚类算法:
上面两个谱聚类算法都用到拉普拉斯矩阵,那么规范的拉普拉斯和非规范的拉普拉斯有什么区别?
谱聚类的算法都要计算拉普拉斯矩阵的特征值和特征向量,但是在实践中规范的拉普拉斯矩阵在实际的聚类效果中更好,能够获得更好的聚类性能。
四、谱聚类算法的实现
建立样本模型和求拉普拉斯矩阵的实现(C++代码):
首先将对应的样本转化成完全图并存在矩阵中:
double sample[N][2]; //存放所有样本点(2维的)
void readSample(char *filename){
FILE *fp;
if((fp=fopen(filename,"r"))==NULL){
perror("fopen");
exit(0);
}
char buf[50]={0};
int i=0;
while(fgets(buf,sizeof(buf),fp)!=NULL){
char *w=strtok(buf," \t");
double x=atof(w);
w=strtok(NULL," \t");
double y=atof(w);
sample[i][0]=x;
sample[i][1]=y;
i++;
memset(buf,0x00,sizeof(buf));}
assert(i==N);
fclose(fp);
}
根据距离公式来计算出各点之间的相似度,计算拉普拉斯矩阵
double** getSimMatrix(){
//为二维矩阵申请空间
double **matrix=getMatrix(N,N);
//计算样本点两两之间的相似度,得到矩阵W
int i,j;
for(i=0;i
for(j=i+1;j
double sim=1.0/(1+dist);
if(sim>T){
matrix[j][i]=sim;
matrix[i][j]=sim;
}}}
//计算L=D-W 求拉普拉斯矩阵
for(j=0;j
for(i=0;i
if(i!=j)
matrix[i][j]=0-matrix[i][j];
}
matrix[j][j]=matrix[j][j]-sum;
}
return matrix;
}
谱聚类算法的应用:
谱聚类算法是一种基于图论的算法,它在图像分割领域中应用非常广泛,对于图像处理的步骤一般分为四步:1、将待分割的图像映射为无向带权完全图。2、计算图对应的矩阵。3、求特征值特征向量。4、聚类。得出分割结果。算法中相似度矩阵由图中各像素之间的相似度构成,在计算彩色图像像素之间的相似度时,通常将图像的颜色特征值与空间距离结合起来求出各像素之间的相似度。
谱聚类算法的不足:
谱聚类算法是基于谱图理论的一类新的聚类算法,能对任意形状的数据样本进行划分,已经被成功应用到图像分割、图像识别(人脸识别)等领域。
但是谱聚类算法自身也有不足的地方:算法的时间复杂度和空间复杂度都是比较大的。
附源代码:
#include
#include
#include"matrix.h"
#include"svd.h"
#define N 19 //样本点个数
#define K 4 //K-Means算法中的K
#define T 0.1 //样本点之间相似度的阈值
double sample[N][2]; //存放所有样本点的坐标(2维的)
void readSample(char *filename){
FILE *fp;
if((fp=fopen(filename,"r"))==NULL){
perror("fopen");
exit(0);
}
char buf[50]={0};
int i=0;
while(fgets(buf,sizeof(buf),fp)!=NULL){
char *w=strtok(buf," \t");
double x=atof(w);
w=strtok(NULL," \t");
double y=atof(w);
sample[i][0]=x;
sample[i][1]=y;
i++;
memset(buf,0x00,sizeof(buf));
}
assert(i==N);
fclose(fp);
}
double** getSimMatrix(){
//为二维矩阵申请空间
double **matrix=getMatrix(N,N);
//计算样本点两两之间的相似度,得到矩阵W
int i,j;
for(i=0;i
for(j=i+1;j
double sim=1.0/(1+dist);
if(sim>T){
matrix[j][i]=sim;
matrix[i][j]=sim;
}
}
}
//计算L=D-W
for(j=0;j
for(i=0;i
if(i!=j)
matrix[i][j]=0-matrix[i][j];
}
matrix[j][j]=matrix[j][j]-sum;
}
return matrix;
}
int main(){
char *file="/home/orisun/data";
readSample(file);
double **L=getSimMatrix();
printMatrix(L,N,N);
double **M=singleVector(L,N,N,5);
printMatrix(M,N,5);
freeMatrix(L,N);
return 0;
}
L已是对称矩阵,直接奇异值分解的得到的就是特征向量
#ifndef _MATRIX_H
#define _MATRIX_H
#include
#include
#include
//初始化一个二维矩阵
double** getMatrix(int rows,int columns){
double **rect=(double**)calloc(rows,sizeof(double*));
int i;
for(i=0;i
return rect;
}
//返回一个单位矩阵
double** getIndentityMatrix(int rows){
double** IM=getMatrix(rows,rows);
int i;
for(i=0;i
return IM;
}
//返回一个矩阵的副本
double** copyMatrix(double** matrix,int rows,int columns){
double** rect=getMatrix(rows,columns);
int i,j;
for(i=0;i
return rect;
}
//从一个一维矩阵得到一个二维矩阵
void getFromArray(double** matrix,int rows,int columns,double *arr){
int i,j,k=0;
for(i=0;i
}
}
}
//打印二维矩阵
void printMatrix(double** matrix,int rows,int columns){
int i,j;
for(i=0;i
}
printf("\n");
}
}
//释放二维矩阵
void freeMatrix(double** matrix,int rows){
int i;
for(i=0;i
free(matrix);
}
//获取二维矩阵的某一行
double* getRow(double **matrix,int rows,int columns,int index){
assert(index
int i;
for(i=0;i
return rect;
}
//获取二维矩阵的某一列
double* getColumn(double **matrix,int rows,int columns,int index){
assert(index
int i;
for(i=0;i
return rect;
}
//设置二维矩阵的某一列
void setColumn(double **matrix,int rows,int columns,int index,double *arr){
assert(index
for(i=0;i
}
//交换矩阵的某两列
void exchangeColumn(double **matrix,int rows,int columns,int i,int j){
assert(i
for(row=0;row
matrix[row][i]=matrix[row][j];
matrix[row][j]=tmp;
}
}
//得到矩阵的转置
double** getTranspose(double **matrix,int rows,int columns){
double **rect=getMatrix(columns,rows);
int i,j;
for(i=0;i
}
}
return rect;
}
//计算两向量内积
double vectorProduct(double *vector1,double *vector2,int len){
double rect=0.0;
int i;
for(i=0;i
return rect;
}
//两个矩阵相乘
double** matrixProduct(double **matrix1,int rows1,int columns1,double **matrix2,int columns2){
double **rect=getMatrix(rows1,columns2);
int i,j;
for(i=0;i
double *vec2=getColumn(matrix2,columns1,columns2,j);
rect[i][j]=vectorProduct(vec1,vec2,columns1);
free(vec1);
free(vec2);
}
}
return rect;
}
//得到某一列元素的平方和
double getColumnNorm(double** matrix,int rows,int columns,int index){
assert(index
double norm=vectorProduct(vector,vector,rows);
free(vector);
return norm;
}
//打印向量
void printVector(double* vector,int len){
int i;
for(i=0;i
printf("\n");
}
#endif
#include"matrix.h"
#define ITERATION 100 //单边Jacobi最大迭代次数
#define THREASHOLD 0.1
//符号函数
int sign(double number) {
if(number<0)
return -1;
else
return 1;
}
//两个向量进行单边Jacobi正交变换
void orthogonalVector(double *Ci,double *Cj,int len1,double *Vi,double *Vj,int len2,int *pass){
double ele=vectorProduct(Ci,Cj,len1);
if(fabs(ele)
*pass=0;
double ele1=vectorProduct(Ci,Ci,len1);
double ele2=vectorProduct(Cj,Cj,len1);
double tao=(ele1-ele2)/(2*ele);
double tan=sign(tao)/(fabs(tao)+sqrt(1+pow(tao,2)));
double cos=1/sqrt(1+pow(tan,2));
double sin=cos*tan;
int row;
for(row=0;row
double var2=Cj[row]*cos-Ci[row]*sin;
Ci[row]=var1;
Cj[row]=var2;
}
for(row=0;row
double var2=Vj[row]*cos-Vi[row]*sin;
Vi[row]=var1;
Vj[row]=var2;
}
}
//矩阵的两列进行单边Jacobi正交变换。V是方阵,行/列数为columns
void orthogonal(double **matrix,int rows,int columns,int i,int j,int *pass,double **V){
assert(i
double* Ci=getColumn(matrix,rows,columns,i);
double* Cj=getColumn(matrix,rows,columns,j);
double* Vi=getColumn(V,columns,columns,i);
double* Vj=getColumn(V,columns,columns,j);
orthogonalVector(Ci,Cj,rows,Vi,Vj,columns,pass);
int row;
for(row=0;row
matrix[row][j]=Cj[row];
}
for(row=0;row
V[row][j]=Vj[row];
}
free(Ci);
free(Cj);
free(Vi);
free(Vj);
}
//循环正交,进行奇异值分解
void hestens_jacobi(double **matrix,int rows,int columns,double **V)
{
int iteration = ITERATION;
while (iteration-- > 0) {
int pass = 1;
int i,j;
for (i = 0; i < columns; ++i) {
for (j = i+1; j < columns; ++j) {
orthogonal(matrix,rows,columns,i,j,&pass,V); //经过多次的迭代正交后,V就求出来了
}
}
if (pass==1) //当任意两列都正交时退出迭代
break;
}
printf("迭代次数:%d\n",ITERATION - iteration);
}
//获取矩阵前n小的奇异向量
double **singleVector(double **A,int rows,int columns,int n){
double **V=getIndentityMatrix(columns);
hestens_jacobi(A,rows,columns,V);
double *singular=(double*)calloc(columns,sizeof(double)); //特征值
int i,j;
for(i=0;i
double norm=sqrt(vectorProduct(vector,vector,rows));
singular[i]=norm;
}
int *sort=(int*)calloc(columns,sizeof(int));
for(i=0;i
for(i=0;i
int minValue=singular[i];
for(j=i+1;j
minIndex=j;
}
}
//交换sigular的第i个和第minIndex个元素
singular[minIndex]=singular[i];
singular[i]=minValue;
//交换sort的第i个和第minIndex个元素
int tmp=sort[minIndex];
sort[minIndex]=sort[i];
sort[i]=tmp;
}
double **rect=getMatrix(rows,n);
for(i=0;i
}
}
freeMatrix(V,columns);
free(sort);
free(singular);
return rect;
}
最后是运行KMeans的Java代码
package ai;
public class Global {
//计算两个向量的欧氏距离
public static double calEuraDist(double[] arr1,double[] arr2,int len){
double result=0.0;
for(int i=0;i
}
return Math.sqrt(result);
}
}
package ai;
public class DataObject {
String docname;
double[] vector;
int cid;
boolean visited;
public DataObject(int len){
vector=new double[len];
}
public String getName() {
return docname;
}
public void setName(String docname) {
this.docname = docname;
}
public double[] getVector() {
return vector;
}
public void setVector(double[] vector) {
this.vector = vector;
}
public int getCid() {
return cid;
}
public void setCid(int cid) {
this.cid = cid;
}
public boolean isVisited() {
return visited;
}
public void setVisited(boolean visited) {
this.visited = visited;
}
}
package ai;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Iterator;
public class DataSource {
ArrayList
int row;
int col;
public void readMatrix(File dataFile) {
try {
FileReader fr = new FileReader(dataFile);
BufferedReader br = new BufferedReader(fr);
String line = br.readLine();
String[] words = line.split("\\s+");
row = Integer.parseInt(words[0]);
// row=1000;
col = Integer.parseInt(words[1]);
objects = new ArrayList
for (int i = 0; i < row; i++) {
DataObject object = new DataObject(col);
line = br.readLine();
words = line.split("\\s+");
for (int j = 0; j < col; j++) {
object.getVector()[j] = Double.parseDouble(words[j]);
}
objects.add(object);
}
br.close();
} catch (IOException e) {
e.printStackTrace();
}
}
public void readRLabel(File file) {
try {
FileReader fr = new FileReader(file);
BufferedReader br = new BufferedReader(fr);
String line = null;
for (int i = 0; i < row; i++) {
line = br.readLine();
objects.get(i).setName(line.trim());
}
} catch (IOException e) {
e.printStackTrace();
}
}
public void printResult(ArrayList
//DBScan是从第1类开始,K-Means是从第0类开始
// for (int i =0; i
System.out.println("=============属于第"+i+"类的有:===========================");
Iterator
while (iter.hasNext()) {
DataObject object = iter.next();
int cid=object.getCid();
if(cid==i){
System.out.println(object.getName());
// switch(Integer.parseInt(object.getName())/1000){
// case 0:
// System.out.println(0);
// break;
// case 1:
// System.out.println(1);
// break;
// case 2:
// System.out.println(2);
// break;
// case 3:
// System.out.println(3);
// break;
// case 4:
// System.out.println(4);
// break;
// case 5:
// System.out.println(5);
// break;
// default:
// System.out.println("Go Out");
// break;
// }
}
}
}
}
}
package ai;
import java.io.File;
import java.util.ArrayList;
import java.util.Iterator;
import java.util.Random;
public class KMeans {
int k; // 指定划分的簇数
double mu; // 迭代终止条件,当各个新质心相对于老质心偏移量小于mu时终止迭代
double[][] center; // 上一次各簇质心的位置
int repeat; // 重复运行次数
double[] crita; // 存放每次运行的满意度
public KMeans(int k, double mu, int repeat, int len) {
this.k = k;
this.mu = mu;
this.repeat = repeat;
center = new double[k][];
for (int i = 0; i < k; i++)
center[i] = new double[len];
crita = new double[repeat];
}
// 初始化k个质心,每个质心是len维的向量,每维均在left--right之间
public void initCenter(int len, ArrayList
Random random = new Random(System.currentTimeMillis());
int[] count = new int[k]; // 记录每个簇有多少个元素
Iterator
while (iter.hasNext()) {
DataObject object = iter.next();
int id = random.nextInt(10000)%k;
count[id]++;
for (int i = 0; i < len; i++)
center[id][i] += object.getVector()[i];
}
for (int i = 0; i < k; i++) {
for (int j = 0; j < len; j++) {
center[i][j] /= count[i];
}
}
}
// 把数据集中的每个点归到离它最近的那个质心
public void classify(ArrayList
Iterator
while (iter.hasNext()) {
DataObject object = iter.next();
double[] vector = object.getVector();
int len = vector.length;
int index = 0;
double neardist = Double.MAX_VALUE;
for (int i = 0; i < k; i++) {
double dist = Global.calEuraDist(vector, center[i], len); // 使用欧氏距离
if (dist < neardist) {
neardist = dist;
index = i;
}
}
object.setCid(index);
}
}
// 重新计算每个簇的质心,并判断终止条件是否满足,如果不满足更新各簇的质心,如果满足就返回true.len是数据的维数
public boolean calNewCenter(ArrayList
boolean end = true;
int[] count = new int[k]; // 记录每个簇有多少个元素
double[][] sum = new double[k][];
for (int i = 0; i < k; i++)
sum[i] = new double[len];
Iterator
while (iter.hasNext()) {
DataObject object = iter.next();
int id = object.getCid();
count[id]++;
for (int i = 0; i < len; i++)
sum[id][i] += object.getVector()[i];
}
for (int i = 0; i < k; i++) {
if (count[i] != 0) {
for (int j = 0; j < len; j++) {
sum[i][j] /= count[i];
}
}
// 簇中不包含任何点,及时调整质心
else {
int a=(i+1)%k;
int b=(i+3)%k;
int c=(i+5)%k;
for (int j = 0; j < len; j++) {
center[i][j] = (center[a][j]+center[b][j]+center[c][j])/3;
}
}
}
for (int i = 0; i < k; i++) {
// 只要有一个质心需要移动的距离超过了mu,就返回false
if (Global.calEuraDist(sum[i], center[i], len) >= mu) {
end = false;
break;
}
}
if (!end) {
for (int i = 0; i < k; i++) {
for (int j = 0; j < len; j++)
center[i][j] = sum[i][j];
}
}
return end;
}
// 计算各簇内数据和方差的加权平均,得出本次聚类的满意度.len是数据的维数
public double getSati(ArrayList
double satisfy = 0.0;
int[] count = new int[k];
double[] ss = new double[k];
Iterator
while (iter.hasNext()) {
DataObject object = iter.next();
int id = object.getCid();
count[id]++;
for (int i = 0; i < len; i++)
ss[id] += Math.pow(object.getVector()[i] - center[id][i], 2.0);
}
for (int i = 0; i < k; i++) {
satisfy += count[i] * ss[i];
}
return satisfy;
}
public double run(int round, DataSource datasource, int len) {
System.out.println("第" + round + "次运行");
initCenter(len,datasource.objects);
classify(datasource.objects);
while (!calNewCenter(datasource.objects, len)) {
classify(datasource.objects);
}
datasource.printResult(datasource.objects, k);
double ss = getSati(datasource.objects, len);
System.out.println("加权方差:" + ss);
return ss;
}
public static void main(String[] args) {
DataSource datasource = new DataSource();
datasource.readMatrix(new File("/home/orisun/test/dot.mat"));
datasource.readRLabel(new File("/home/orisun/test/dot.rlabel"));
int len = datasource.col;
// 划分为4个簇,质心移动小于1E-8时终止迭代,重复运行7次
KMeans km = new KMeans(4, 1E-10, 7, len);
int index = 0;
double minsa = Double.MAX_VALUE;
for (int i = 0; i < km.repeat; i++) {
double ss = km.run(i, datasource, len);
if (ss < minsa) {
minsa = ss;
index = i;
}
}
System.out.println("最好的结果是第" + index + "次。");
}
}
谢谢!