标号法求解单源最短路径

1. 问题描述

给定一个图结构，包含n个点，e条边，求解源点 s 到汇点 t 的最短路径及长度，以及源点 s 到前1000个点的最短路径长度。

数据文件"union.txt"，格式为：

start_id,end_id,weight,start_x,start_y,end_x,end_y
1,101043,540,567.988263,99.564119,567.988263,100.104119
......

2. 算法策略

算法模拟了标号法的求解过程。首先有一个优先队列，队列种中的元素为（点号，权值），初始状态把源点（权值为0）入队，然后不断进行BFS，从优先队列里取出权值最小的元素（如果访问过则重新取下一个元素），访问该元素，标记位置1，对其相邻的结点进行“松弛”，更新它们的当前权值，更新它们的距离数组dist和路径数组path，并将它们全部入队，进行下一轮操作，从队列中取元素......队列为空时路径求解完成。

需要注意的是，某个结点可能会多次入队，可能会被多次松弛，但只会被访问一次（由标记数组决定）。

由dist数组和path数组可得到源点 s 到任意一点 t 的最短路径及长度。求解完成后，dist数组本身即更新为最短路径长度。由于path[i]是i的前驱结点，可间接得到路径。

3. 优化操作

因为涉及大量数据的 I/O，为加快读写速度，使用C语法进行 I/O操作，而不用,,中的流，可节约至少一半的 I/O 时间。初始化用memset代替循环初始化。另外加了实时进度显示与时间统计。

4. 代码实现

#include "stdio.h"
#include "windows.h"
#include 
#include 
#include 
#include 
using namespace std;

#define MAXN 195234 //0 1 ... 195233
#define MAXW 0x3f3f3f3f //最大权重

typedef struct WNode{
	int id;
	int cur_w;
	bool operator<(const WNode& n)const{
		return cur_w>n.cur_w;
	}
	WNode(int id,int cur_w):id(id),cur_w(cur_w){}
}WNode;

//Graph[i]中存放的是 与i号结点相邻的 结点们的编号j以及对应权重w, Graph[i]={pair,...}
vector > Graph[MAXN];
bool visit[MAXN];
int path[MAXN];
int dist[MAXN];

int s,t; //源点,汇点
clock_t start,finish;

//读入文件进行初始化
bool Initialize(){
	printf("Input the starting point: ");
	scanf("%d",&s);
	printf("Input the ending   point: ");
	scanf("%d",&t);

	printf("\nInputing data...\n");
	start=clock();
	FILE* fp=fopen("union.txt","r");
	if(fp==NULL){
		printf("File open error./n");
		return -1;
	}
	int sid,tid,w;
	double sx,sy,tx,ty;
	fscanf(fp,"%*[^\n]%*c");//跳过第一行
	while(true){
		fscanf(fp,"%d,%d,%d,%lf,%lf,%lf,%lf",&sid,&tid,&w,&sx,&sy,&tx,&ty);
		Graph[sid].push_back(make_pair(tid,w));
		//printf("%d %d %d\n",sid,tid,w);
		if(sid%1000==0){
			printf("\r[%.2f%%]",sid/195233.0*100);
			fflush(stdout);
		}
		if(sid==195233){
			printf("\r[%.2f%%]",sid/195233.0*100);
			finish=clock();
			printf("\nData input successfully.\n");
			printf("Total time is %.2fs\n.",(double)(finish-start)/CLOCKS_PER_SEC);
			break;
		}
	}
	fclose(fp);
	return true;
}

//求解最短路径
void ShortestPath(int s){
	printf("\nSolving shortest path...\n");
	start=clock();

	memset(path,0,sizeof(path));
	memset(visit,0,sizeof(visit));
	memset(dist,MAXW,sizeof(dist));	
	priority_queue qu;
	qu.push(WNode(s,0));
	path[s]=0;
	dist[s]=0;
	int sumvisit=0;//记录进度

	while(!qu.empty()){
		WNode cur=qu.top();
		qu.pop();
		if(visit[cur.id])continue;
		visit[cur.id]=1;
		sumvisit++;
		if(sumvisit%500==0){
			printf("\r[%.2f%%]",sumvisit/195233.0*100);
			fflush(stdout);
		}
		
		for(int i=0;i tmp=Graph[cur.id][i];
			if(!visit[tmp.first]){  //将未访问过的入队
				qu.push(WNode(tmp.first,tmp.second+cur.cur_w));
			}
			if(tmp.second+cur.cur_w < dist[tmp.first]){  //松弛
				dist[tmp.first]=tmp.second+cur.cur_w;
				path[tmp.first]=cur.id;
			}
		}
	}
	printf("\r[100.00%%]\n");
	printf("Path solved successfully.\n");
	finish=clock();
	printf("Total time is %.2fs.\n",(double)(finish-start)/CLOCKS_PER_SEC);
}

//显示路径，反向输出
void DispPath(int t){
	printf("\nPath from %d to %d:\n",s,t);
	printf("Shortest path length is %d.\n\n",dist[t]);
	stack tmps;
	int j=t;
	while(j>0){
		tmps.push(j);
		j=path[j];
	}
	while(tmps.size()>1){
		printf("%d->",tmps.top());
		tmps.pop();
	}
	printf("%d\n",tmps.top()); //不输出最后一个箭头
	tmps.pop();
}

//将源点 s 与前 10000 个点的最短距离输出到文件
void ToFile(){
	FILE* fp;
	char str[20];
	itoa(s,str,10);
	strcat(str,".txt");//生成文件名
	fp=fopen(str,"w");
	fprintf(fp,"start_id,end_id,dist\n");
	for(int i=1;i<=10000;i++){
		if(dist[i]!=0x3f3f3f3f)
			fprintf(fp,"%d,%d,%d\n",s,i,dist[i]);
		else
			fprintf(fp,"%d,%d,NaN\n",s,i);
	}
	fclose(fp);
}

int _tmain(int argc, _TCHAR* argv[])
{
	Initialize();	
	ShortestPath(s);
	ToFile();
	DispPath(t);
	return 0;
}

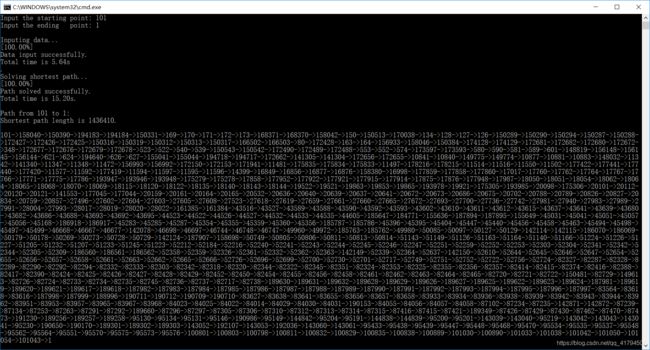
5. 运行结果

（1）最短路径（101->1）：

（2）源点到前10000个点的距离：

start_id,end_id,dist
101,1,1436410
101,2,1302440
101,3,1334756
101,4,1334893
101,5,1293080
......