利用matlab实现扩展卡尔曼滤波（EKF）与无迹卡尔曼滤波（UKF）

例题

将下例进行EKF和UKF代码实现，进行仿真复现。

EKF算法模型

clc;
clear;
%测量值模拟
T=0.05;%滤波周期
T_go=10;%滤波时间
N=T_go/T;%观测次数
t=0:T:T_go-T;%假定输出序列（供画图用）
x=zeros(2,N);
z=zeros(2,N);
x(:,1)=[1;0];%真值初始值
mu=[0;0];
Q=[0.01,0;0,0.0001];
R=[0.1,0;0,0.1];

rng(1);
w=mvnrnd(mu,Q,N)';
v=mvnrnd(mu,R,N)';
for k=1:N-1
    x1=x(1,k);x2=x(2,k);
    w1=w(1,k);w2=w(2,k);
    x(:,k+1)=[x1+T*x2+w1;-10*T*sin(x1)+(1-T)*x2+w2];
    x1=x(1,k+1);x2=x(2,k+1);
    v1=v(1,k+1);v2=v(2,k+1);
    z(:,k+1)=[2*sin(x1/2)+v1;x1/2+v2];
end
%EKF估计
xk=zeros(2,N);
xk(:,1)=[1;0];
Pk=[1,0;0,1];
for k=1:N-1
    x1=xk(1,k);x2=xk(2,k);
    Fai=[1,T;-10*T*cos(x1),1-T];
    xk(:,k+1)=[x1+T*x2;-10*T*sin(x1)+(1-T)*x2];
    Pk=Fai*Pk*Fai'+Q;
    x1=xk(1,k+1);x2=xk(2,k+1);
    Hk=[cos(x1/2),0;1/2,0];
    Kk=Pk*Hk'/(Hk*Pk*Hk'+R);
    xk(:,k+1)=xk(:,k+1)+Kk*(z(:,k+1)-[2*sin(x1/2);x1/2]);
    Pk=(eye(2)-Kk*Hk)*Pk*(eye(2)-Kk*Hk)'+Kk*R*Kk';
end

subplot(2,1,1);
plot(t,x(1,:),'-r',t,z(1,:),'-g',t,xk(1,:),'-b');
xlabel('t');
ylabel('x1');
subplot(2,1,2);
plot(t,x(2,:),'-r',t,z(2,:),'-g',t,xk(2,:),'-b');
xlabel('t');
ylabel('x2');
legend('状态值','测量值','EKF');

输出结果：

UKF算法模型

clc;
clear;
%测量值模拟
T=0.05;%滤波周期
T_go=10;%滤波时间
N=T_go/T;%观测次数
t=0:T:T_go-T;%假定输出序列（供画图用）
x=zeros(2,N);
z=zeros(2,N);
x(:,1)=[1;0];%真值初始值
mu=[0;0];
Q=[0.01,0;0,0.0001];
R=[0.1,0;0,0.1];

rng(1);
w=mvnrnd(mu,Q,N)';
v=mvnrnd(mu,R,N)';
for k=1:N-1
    x1=x(1,k);x2=x(2,k);
    w1=w(1,k);w2=w(2,k);
    x(:,k+1)=[x1+T*x2+w1;-10*T*sin(x1)+(1-T)*x2+w2];
    x1=x(1,k+1);x2=x(2,k+1);
    v1=v(1,k+1);v2=v(2,k+1);
    z(:,k+1)=[2*sin(x1/2)+v1;x1/2+v2];
end

%UKF估计
alpha=0.1;
beta=2;
kappa=1;
n=2;%状态维数
lamda=alpha^2*(n+kappa)-n;
xk=zeros(2,N);

%1.初始化
xk(:,1)=[1;0];
Pk=[1,0;0,1];
wm=zeros(1,5);
wc=zeros(1,5);
wm(1)=lamda/(n+lamda);
wc(1)=lamda/(n+lamda)+1-alpha^2+beta;
for i=2:2*n+1
    wm(i)=1/(2*(n+lamda));
    wc(i)=1/(2*(n+lamda));
end

for k=1:N-1
%2.计算k-1时刻采样点和权值
    xsigma=zeros(2,5);
    xsigma(:,1)=xk(:,k);
    xsigma(:,2)=xk(:,k)+sqrt(n+lamda)*sqrt(Pk(:,1));
    xsigma(:,3)=xk(:,k)+sqrt(n+lamda)*sqrt(Pk(:,2));
    xsigma(:,4)=xk(:,k)-sqrt(n+lamda)*sqrt(Pk(:,1));
    xsigma(:,5)=xk(:,k)-sqrt(n+lamda)*sqrt(Pk(:,2));
%3.计算k时刻的一步预测模型值
    xsigmapre=zeros(2,5);
    for i=1:5
        xsigmapre(:,i)=[xsigma(1,i)+T*xsigma(2,i);-10*T*sin(xsigma(1,i))+(1-T)*xsigma(2,i)];
    end
    xkpre=xsigmapre*wm';
    Pkpre=Q;
    for i=1:5
        Pkpre=Pkpre+wc(i)*(xsigmapre(:,i)-xkpre)*(xsigmapre(:,i)-xkpre)';
    end
%4.计算k时刻的一步预测样本点（重新采样）    
%     xsigma(:,1)=xkpre;
%     xsigma(:,2)=xkpre+sqrt(n+lamda)*sqrt(Pkpre(1));
%     xsigma(:,3)=xkpre+sqrt(n+lamda)*sqrt(Pkpre(2));
%     xsigma(:,4)=xkpre-sqrt(n+lamda)*sqrt(Pkpre(1));
%     xsigma(:,5)=xkpre-sqrt(n+lamda)*sqrt(Pkpre(2));
%5.计算k时刻的预测量测值
    zsigmapre=zeros(2,5);
    for i=1:5
       zsigmapre(:,i)=[2*sin(xsigma(1,i)/2);xsigma(1,i)/2] ;  
    end
    zkpre=zsigmapre*wm';
    Pzzk=R;
    Pxzk=zeros(2);
    for i=1:5
        Pzzk=Pzzk+wc(i)*(zsigmapre(:,i)-zkpre)*(zsigmapre(:,i)-zkpre)';
        Pxzk=Pxzk+wc(i)*(xsigma(:,i)-xkpre)*(zsigmapre(:,i)-zkpre)';
    end
%6.量测更新
    Kk=Pxzk/Pzzk;
    xkpre=xkpre+Kk*(z(:,k+1)-zkpre);
    Pkpre=Pkpre-Kk*Pzzk*Kk';
    
    xk(:,k+1)=xkpre;
    Pk=Pkpre;
end

subplot(2,1,1);
plot(t,x(1,:),'-r',t,z(1,:),'-g',t,xk(1,:),'-b');
xlabel('t');
ylabel('x1');
subplot(2,1,2);
plot(t,x(2,:),'-r',t,z(2,:),'-g',t,xk(2,:),'-b');
xlabel('t');
ylabel('x2');
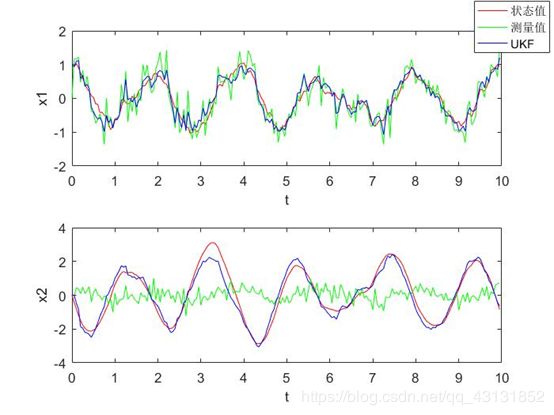
legend('状态值','测量值','UKF');

输出结果：