最短路问题之Dijkstra算法
最短路问题之Dijkstra算法
- 最短路性质
- 算法步骤
- 例题(无向图)
- Python代码
- Matlab代码
- Python图论包networkx
最短路性质
在图 G G G中,记 ( v i , v j ) k (v_i,v_j)_k (vi,vj)k为点 v i , v j v_i, v_j vi,vj之间的第 k k k条路径, ∣ ( v i , v j ) k ∣ |(v_i,v_j)_k| ∣(vi,vj)k∣为点 v i , v j v_i, v_j vi,vj之间沿着第 k k k条路径的权和。设从点 v 0 v_0 v0到点 v n v_n vn之间的最短路径 ( v 0 , v n ) k 0 (v_0,v_n)_{k_0} (v0,vn)k0为
v 0 → . . . → v n , v_0 \rightarrow ... \rightarrow v_n, v0→...→vn, v i , v j v_i, v_j vi,vj是路径中的两点,则有
∣ ( v i , v j ) k 0 ∣ = min ∀ k ∣ ( v i , v j ) k ∣ , |(v_i, v_j)_{k_0}| = \min_{\forall k}|(v_i, v_j)_k|, ∣(vi,vj)k0∣=∀kmin∣(vi,vj)k∣,即最短路的任一段也是最短路。
算法步骤
记 V V V为全部点的集合, W W W为带权邻接矩阵, W ( u , v ) W(u,v) W(u,v)表示从点 u u u到点 v v v的权。记起始点为 u 0 u_0 u0。
- 初始化:令 S = { u 0 } , S ‾ = V ∖ S S = \{u_0\}, \overline S = V\setminus S S={u0},S=V∖S,给点 u 0 u_0 u0标记在最短路中的距离 d ( u 0 ) = 0 d(u_0)=0 d(u0)=0;
- 找出 S S S里每一个点 u k u_k uk的相邻点集 { v i } k \{v_{i}\}_k {vi}k,找出相应的 u k 0 , v o p t ∈ ∪ { v i } k , s . t . u_{k_0},v_{opt} \in \cup \{v_{i}\}_k,\ s.t. uk0,vopt∈∪{vi}k, s.t.
d ( u k 0 ) + W ( u k 0 , v o p t ) = min u k ∈ S , v t ∈ { v i } k d ( u k ) + W ( u k , v t ) ; d(u_{k_0}) + W(u_{k_0}, v_{opt}) = \min _{u_k \in S,\ v_t \in \{v_{i}\}_k} d(u_k) + W(u_k, v_t); d(uk0)+W(uk0,vopt)=uk∈S, vt∈{vi}kmind(uk)+W(uk,vt); - 给点 v o p t v_{opt} vopt标记在最短路中的距离 d ( v o p t ) = d ( u k 0 ) + W ( u k 0 , v o p t ) d(v_{opt})=d(u_{k_0}) + W(u_{k_0}, v_{opt}) d(vopt)=d(uk0)+W(uk0,vopt),该点的父点即为 u k 0 u_{k_0} uk0,令 S = S ∪ { v o p t } , S ‾ = S ∖ { v o p t } S=S\cup \{v_{opt}\}, \overline S = S \setminus \{v_{opt}\} S=S∪{vopt},S=S∖{vopt};
- 若 S ‾ ≠ ∅ \overline S \neq \varnothing S=∅,则返回步骤2)。
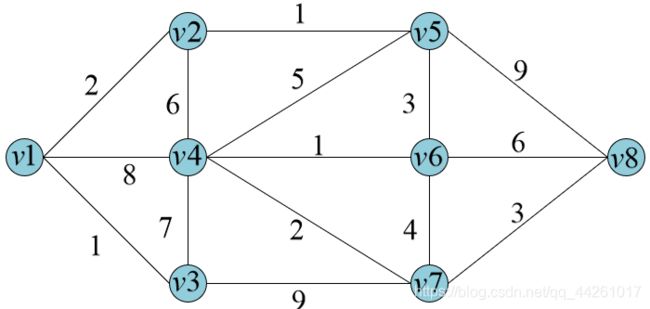
例题(无向图)
Python代码
from math import inf
import numpy as np
from prettytable import PrettyTable
# 输入和设置算法参数
N, N_start = 8, 1 # 点的总数,起始点编号
l_v, z_v = np.zeros(N), np.ones(N) # 从起始点到其他各点的权,父点列表
V, S = [n + 1 for n in range(N)], [N_start] # 全部点集,现包括点集
S_bar = [n + 1 for n in range(N)] # 还未包括点集
S_bar.remove(N_start)
D = np.array(
[[0, 2, 1, 8, inf, inf, inf, inf],
[2, 0, inf, 6, 1, inf, inf, inf],
[1, inf, 0, 7, inf, inf, 9, inf],
[8, 6, 7, 0, 5, 1, 2, inf],
[inf, 1, inf, 5, 0, 3, inf, 9],
[inf, inf, inf, 1, 3, 0, 4, 6],
[inf, inf, 9, 2, inf, 4, 0, 3],
[inf, inf, inf, inf, 9, 6, 3, 0]]
) # 带权邻接矩阵
# 初始化算法步骤表
table = ['Iter']
for i in range(N):
table.append('v' + str(i + 1))
table = PrettyTable(table)
table.add_row([0, 0] + [inf] * (N - 1))
# 初始化迭代次数
k_iter = 1
# 进入算法迭代主体
while S_bar:
line = [inf] * N
dist_new = inf
for i in range(len(S)):
for j in [index for (index, value) in enumerate(D[S[i]])]:
if (j + 1) in S_bar:
if D[S[i] - 1, j] != inf:
dist = l_v[S[i] - 1] + D[S[i] - 1, j]
line[j] = min(line[j], dist)
if dist < dist_new:
dist_new = dist
father_point, new_point = S[i], j + 1
else:
line[j] = np.nan
l_v[new_point - 1], z_v[new_point - 1] = dist_new, father_point
S.append(new_point)
S_bar.remove(new_point)
table.add_row([k_iter] + line)
k_iter += 1
# 输出算法步骤表
print(table)
# 输出最短路信息
print('起始点到其他各点的权l_v:\n', l_v)
print('最短路中各点的父点:\n', z_v)
结果:
+------+-----+-----+-----+-----+-----+-----+------+------+
| Iter | v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 |
+------+-----+-----+-----+-----+-----+-----+------+------+
| 0 | 0 | inf | inf | inf | inf | inf | inf | inf |
| 1 | nan | 2.0 | 1.0 | 8.0 | inf | inf | inf | inf |
| 2 | nan | 2.0 | nan | 8.0 | inf | inf | 10.0 | inf |
| 3 | nan | nan | nan | 8.0 | 3.0 | inf | 10.0 | inf |
| 4 | nan | nan | nan | 8.0 | nan | 6.0 | 10.0 | 12.0 |
| 5 | nan | nan | nan | 7.0 | nan | nan | 10.0 | 12.0 |
| 6 | nan | nan | nan | nan | nan | nan | 9.0 | 12.0 |
| 7 | nan | nan | nan | nan | nan | nan | nan | 12.0 |
+------+-----+-----+-----+-----+-----+-----+------+------+
起始点到其他各点的权l_v:
[ 0. 2. 1. 7. 3. 6. 9. 12.]
最短路中各点的父点:
[1. 1. 1. 6. 2. 5. 4. 5.]
Matlab代码
D = [0 2 1 8 inf inf inf inf;
2 0 inf 6 1 inf inf inf;
1 inf 0 7 inf inf 9 inf;
8 6 7 0 5 1 2 inf;
inf 1 inf 5 0 3 inf 9;
inf inf inf 1 3 0 4 6;
inf inf 9 2 inf 4 0 3;
inf inf inf inf 9 6 3 0];
start_point = 1;
S = [start_point];
S_bar = 1:length(D); S_bar(start_point) = [];
L = cellmat(1,length(D),1,1,0); Z=L; Z{1}=1;
Tab = table(1, 0, inf, inf, inf, inf, inf, inf, inf,...
'VariableNames', {'Iter','V1','V2','V3','V4','V5','V6','V7','V8'});
while ~isempty(S_bar)
t = cellmat(1,length(D),1,1,inf);
dist=inf; new_point=[]; father_point=[];
for i = S
for j = S_bar
t1 = L{i}+D(i,j);
t{1,j} = min(t{1,j}, t1);
if t1<dist
dist = t1; new_point=j; father_point=i;
end
end
end
S = [S, new_point]; S_bar(S_bar==new_point)=[];
L{new_point} = dist;
Z{new_point} = father_point;
Tab(end+1, :) = [{Tab.Iter(end)+1},t];
end
disp(Tab)
disp([{'L(v)'},L])
disp([{'Z(v)'},Z])
结果:
Iter V1 V2 V3 V4 V5 V6 V7 V8
____ ___ ___ ___ ___ ___ ___ ___ ___
1 0 Inf Inf Inf Inf Inf Inf Inf
2 Inf 2 1 8 Inf Inf Inf Inf
3 Inf 2 Inf 8 Inf Inf 10 Inf
4 Inf Inf Inf 8 3 Inf 10 Inf
5 Inf Inf Inf 8 Inf 6 10 12
6 Inf Inf Inf 7 Inf Inf 10 12
7 Inf Inf Inf Inf Inf Inf 9 12
8 Inf Inf Inf Inf Inf Inf Inf 12
'L(v)' [0] [2] [1] [7] [3] [6] [9] [12]
'Z(v)' [1] [1] [1] [6] [2] [5] [4] [5]
Python图论包networkx
import networkx as nx
import matplotlib.pyplot as plt
# 画原题图像
G = nx.Graph()
G.add_weighted_edges_from([('v1', 'v2', 2), ('v1', 'v3', 1), ('v1', 'v4', 8),
('v2', 'v4', 6), ('v4', 'v3', 7), ('v2', 'v5', 1),
('v4', 'v5', 5), ('v4', 'v6', 1), ('v4', 'v7', 2),
('v3', 'v7', 9), ('v5', 'v6', 3), ('v6', 'v7', 4),
('v5', 'v8', 9), ('v6', 'v8', 6), ('v7', 'v8', 3)])
edge_labels = dict([((u, v), d['weight']) for u, v, d in G.edges(data=True)])
pos = nx.spring_layout(G)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=15)
nx.draw_networkx(G, pos, node_size=400)
plt.show()
# 求解题目
mat = nx.to_numpy_matrix(G)
print(mat)
print('dijkstra方法寻找最短路径:')
path = nx.dijkstra_path(G, source='v1', target='v8')
print('节点v1到v8的路径:', path)
print('dijkstra方法寻找最短距离:')
distance = nx.dijkstra_path_length(G, source='v1', target='v8')
print('节点v1到v8的距离为:', distance)
结果:
[[0. 2. 1. 8. 0. 0. 0. 0.]
[2. 0. 0. 6. 1. 0. 0. 0.]
[1. 0. 0. 7. 0. 0. 9. 0.]
[8. 6. 7. 0. 5. 1. 2. 0.]
[0. 1. 0. 5. 0. 3. 0. 9.]
[0. 0. 0. 1. 3. 0. 4. 6.]
[0. 0. 9. 2. 0. 4. 0. 3.]
[0. 0. 0. 0. 9. 6. 3. 0.]]
dijkstra方法寻找最短路径:
节点v1到v8的路径: ['v1', 'v2', 'v5', 'v8']
dijkstra方法寻找最短距离:
节点v1到v8的距离为: 12