极客讲堂 - 数据结构与算法之美 - 回溯算法,初识动态规划,动态规划理论,动态规划实战,拓扑排序,最短路径
39 | 回溯算法
1. 实际上一个类似枚举的搜索尝试过程。按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择。
2. 回溯算法非常适合用递归代码实现
3. 实现的过程中,剪枝操作是提高回溯效率的一种技巧 (不符合条件的就抛弃掉)
40 | 初识动态规划
1. 0-1背包问题,用回溯算法的话时间复杂度是O(2^n),n是物品个数。
用动态规划法是O(m*w),n 表示物品个数,w 表示背包可以承载的总重量。
2. 动态规划法,就是用一个二维数组来记录每层可以达到的状态,然后找出最理想的那个数值。再倒推选用哪个物品的组合。
但其实,用一维数组也可以。
3. 动态规划法,是空间换时间的方式。
附加:
1. 在链表这一节:单链表反转,链表中环的检测,两个有序的链表合并,删除链表倒数第 n 个结点,求链表的中间结点等。
2. 在栈这一节,在函数调用中的应用,在表达式求值中的应用,在括号匹配中的应用。
3. 在排序这一节,如何在 O(n) 的时间复杂度内查找一个无序数组中的第 K 大元素。
4. 在二分查找这一节,二分查找的四个变体。
41 | 动态规划理论
1. 什么样的问题适合用动态规划解决? 符合 “一个模型三个特征” 的问题
(1) 一个模型: 多阶段决策最优解
解决问题需经历多个决策阶段;每个阶段对应一组状态;寻找一组决策序列,获得最优解。
(2) 特征1: 最优子结构
可以通过子问题最优解,推导上层问题最优解。
(3) 特征2: 无后效性
某阶段状态一旦确定,就不受之后阶段的决策影响。
(4) 特征3: 重复子问题
不同的决策序列,到达某个相同的阶段时,可能会产生重复的状态。
2. 动态规划解题思路一: 状态转移表法
(1) 大概思路: 画状态转移表 => 根据递推关系填表 => 将填表过程翻译成代码
(2) 大部分状态表是二维的,适合使用这个方法。
(3) 如果问题的状态比较复杂,需要多个变量来表示,那就不适合用这个方法。
3. 动态规划解题思路二: 状态转移方程法
关键是写出状态转移方程。 就是如何从子状态的数值转化为上一层状态。
4. 四种算法思想比较分析: 贪心、分治、回溯和动态规划
(1) 回溯算法:是个“万金油”,穷举所有的情况,然后对比得到最优解。
时间复杂度指数级别的,只能解决小规模数据。
(2) 动态规划:高效,但不是所有问题都适用。 必须满足三个条件:最优子结构,无后效性,重复子问题。
(3) 分治算法:没有明显的层次子结构。
(4) 贪心算法:动态规划算法的一种特殊情况。必须满足三个条件:最优子结构,无后效性,贪心选择性。
贪心选择性意思:通过局部最优的选择,能产生全局的最优选择。
算法思想:每一个阶段,我们都选择当前看起来最优的决策,所有阶段的决策完成之后,最终由这些局部最优解构成全局最优 解。
42 | 动态规划实战:如何实现搜索引擎中的拼写纠错功能?
1. 通过 量化两个字符串的相似度 的方式。
量化的具体方式是:编辑距离。 即将一个字符串转化为另一个字符串,至少需要编辑的次数(增、删、替换).
2. 编辑距离的两种计算方式:莱文斯坦距离 和 最长公共子串长度
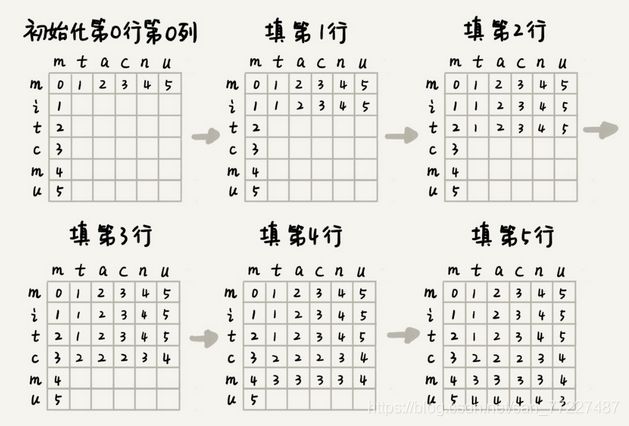
3. 计算莱文斯坦距离 :使用动态规划的方法,将一个字符串如何变成另一字符串 (这个目标字符串不能被修改),并计算次数。
(1) 比较两个字符串,当遇到不相同时,就是一个子问题。通过计算增删改,来进入下一个子问题。
(2) 列一个二维表,两个字符串分别是两维。表格的值就是莱文斯坦距离。
(3) 可以逐层计算,下一层的值可以根据上一层获得。
4. 计算最长公共子串长度:使用动态规划的方法,将两个字符串变成一样的新字符串 (期间两个字符串都可以修改),并计算次数
(1) 比较两个字符串,当遇到不相同时,就是一个子问题。通过计算增删(没有改),来进入下一个子问题。
(2) 用状态转移方程写出来,并转换成代码。
(3) 执行计算。
5. 方法结论: 输入拼写错误的单词时,就拿这个单词跟词库中的单词一一进行比较,计算编辑距离,将编辑距离最小的单词,
作为纠正之后的单词。。
6. 优化策略:
(1) 取出编辑距离最小的 TOP 10,根据单词热度优先选择。
(2) 两种方法一起用,再取TOP 10
(3) 词库可以放到多台机器上,让多台机器并行计算编辑距离。
7. 原文地址:https://m.toutiaoimg.cn/group/6644470519137632263/?iid=57686364204&app=news_article×tamp=1548417216&tt_from=weixin&utm_source=weixin&utm_medium=toutiao_ios&utm_campaign=client_share&wxshare_count=1
43 | 拓扑排序:如何确定代码源文件的编译依赖关系?
1. 数据建模:
把源文件与源文件之间的依赖关系,抽象成一个有向图。
每个源文件对应图中的一个顶点,源文件之间的依赖关系就是顶点之间的边。
这个图不仅要是有向图,还要是一个有向无环图。一旦出现环,拓扑排序就无法工作了。
2. 拓扑排序有两种实现方法:Kahn 算法 和 DFS 深度优先搜索算法
2.1 Kahn 算法:
(1) 从图结构中,找出入度为0的顶点,输出到结果序列中,删除这些顶点。
(2) 这些顶点指向的顶点,入度都减1。
(3) 重复(1) (2)的过程,直至所有顶点都被输出到序列。
2.2 DFS 深度优先搜索算法
(1) 基于图结构构建逆邻接表。为了可以从高层开始遍历顶点。
(2) 递归处理每个顶点。把依赖的顶点都输出了,再输出自己。
3. 算法复杂度:上面的两个算法的时间复杂度都是O(V+E)(V 表示顶点个数,E 表示边的个数)
4. 环的检测:
(1) Kahn 算法:如果输出的结果序列的顶点数小于图中的顶点数,那就存在环。
(2) 深度优先搜索算法:顶点被第二次访问的话,就存在环。
44 | 最短路径:地图软件是如何计算出最优出行路径的?
1. 数据建模:
(1) 地图抽象成图,每个岔路口看作一个顶点,岔路口与岔路口之间的路看作一条边,路的长度就是边的权重。
(2) 整个地图就被抽象成一个有向有权图。 (从起点开始,走每个岔路口都是能到达终点的,不能到达的不要包括进内)
(3) 求解问题转化为:求两个顶点间的最短路径
2. 使用Dijkstra (迪杰斯特拉)算法求解最短路径:
(1) 从起点开始,遍历它能到达的所有顶点。并记录这些顶点的权值。广度遍历的方式,重复执行下去。
(2) 当出现重复到达同一顶点并权值更小时,就更新这个权值。
(3) 重复执行(1)(2),直至到达终点。 最短路径是每次都走权值最小的顶点(贪心算法思路)
3. 时间复杂度:操作包括遍历所有边,和把权值插入到小根堆,所以复杂度=O(E) * O(logV)。 (E是边的个数,V是顶点个数)