AtCoder Beginner Contest 131 题解
A - Security
Time Limit: 2 sec / Memory Limit: 1024 MB
Score : 100100 points
Problem Statement
The door of Snuke's laboratory is locked with a security code.
The security code is a 44-digit number. We say the security code is hard to enter when it contains two consecutive digits that are the same.
You are given the current security code SS. If SS is hard to enter, print Bad; otherwise, print Good.
Constraints
- SS is a 44-character string consisting of digits.
Input
Input is given from Standard Input in the following format:
SS
Output
If SS is hard to enter, print Bad; otherwise, print Good.
Sample Input 1 Copy
Copy
3776
Sample Output 1 Copy
Copy
Bad
The second and third digits are the same, so 37763776 is hard to enter.
Sample Input 2 Copy
Copy
8080
Sample Output 2 Copy
Copy
Good
There are no two consecutive digits that are the same, so 80808080 is not hard to enter.
Sample Input 3 Copy
Copy
1333
Sample Output 3 Copy
Copy
Bad
Sample Input 4 Copy
Copy
0024
Sample Output 4 Copy
Copy
Bad
太水
#include
using namespace std;
typedef long long LL;
const int N=100005;
int a[N];
int n;
int main()
{
// scanf("%d",&n);
string s;
cin>>s;
for(int i=0;i
B - Bite Eating
Time Limit: 2 sec / Memory Limit: 1024 MB
Score : 200200 points
Problem Statement
You have NN apples, called Apple 11, Apple 22, Apple 33, ..., Apple NN. The flavor of Apple ii is L+i−1L+i−1, which can be negative.
You can make an apple pie using one or more of the apples. The flavor of the apple pie will be the sum of the flavors of the apples used.
You planned to make an apple pie using all of the apples, but being hungry tempts you to eat one of them, which can no longer be used to make the apple pie.
You want to make an apple pie that is as similar as possible to the one that you planned to make. Thus, you will choose the apple to eat so that the flavor of the apple pie made of the remaining N−1N−1 apples will have the smallest possible absolute difference from the flavor of the apple pie made of all the NN apples.
Find the flavor of the apple pie made of the remaining N−1N−1 apples when you choose the apple to eat as above.
We can prove that this value is uniquely determined.
Constraints
- 2≤N≤2002≤N≤200
- −100≤L≤100−100≤L≤100
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
NN LL
Output
Find the flavor of the apple pie made of the remaining N−1N−1 apples when you optimally choose the apple to eat.
Sample Input 1 Copy
Copy
5 2
Sample Output 1 Copy
Copy
18
The flavors of Apple 11, 22, 33, 44, and 55 are 22, 33, 44, 55, and 66, respectively. The optimal choice is to eat Apple 11, so the answer is 3+4+5+6=183+4+5+6=18.
Sample Input 2 Copy
Copy
3 -1
Sample Output 2 Copy
Copy
0
The flavors of Apple 11, 22, and 33 are −1−1, 00, and 11, respectively. The optimal choice is to eat Apple 22, so the answer is (−1)+1=0(−1)+1=0.
Sample Input 3 Copy
Copy
30 -50
Sample Output 3 Copy
Copy
-1044也水
#include
using namespace std;
typedef long long LL;
const int N=100005;
int a[N];
int n,L;
int main()
{
scanf("%d%d",&n,&L);
int sum=0;
for(int i=1;i<=n;i++)
{
a[i]=L+i-1;
sum+=a[i];
}
int sum1=sum;
int ans;
int cha=1e9;
for(int i=1;i<=n;i++)
{
sum1=sum;
sum1-=a[i];
if(abs(sum1-sum)
C - Anti-Division
Time Limit: 2 sec / Memory Limit: 1024 MB
Score : 300300 points
Problem Statement
You are given four integers AA, BB, CC, and DD. Find the number of integers between AA and BB (inclusive) that can be evenly divided by neither CC nor DD.
Constraints
- 1≤A≤B≤10181≤A≤B≤1018
- 1≤C,D≤1091≤C,D≤109
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
AA BB CC DD
Output
Print the number of integers between AA and BB (inclusive) that can be evenly divided by neither CC nor DD.
Sample Input 1 Copy
Copy
4 9 2 3
Sample Output 1 Copy
Copy
2
55 and 77 satisfy the condition.
Sample Input 2 Copy
Copy
10 40 6 8
Sample Output 2 Copy
Copy
23
Sample Input 3 Copy
Copy
314159265358979323 846264338327950288 419716939 937510582
Sample Output 3 Copy
Copy
532105071133627368题意:
求[A,B]里既不能整除C又不能整除D的数。
分析:
(A,B](左边取不到)里可以整除C的数有B/C-A/C个,那答案就出来了
B/C-A/C+B/D-A/D-(B/e-A/e)(e为cd最小公倍数)
在判断一下左边界A,总的一减即可。
#include
using namespace std;
typedef long long LL;
const int N=100005;
//int a[N];
int n,L ;
LL gcd(LL a,LL b)
{
return a == 0 ? b : gcd(b % a, a);
}
LL a,b,c,d;
int main()
{
cin>>a>>b>>c>>d;
LL ans=b/c-a/c+b/d-a/d-(b/(c*d/gcd(c,d))-a/(c*d/gcd(c,d)));
if(a%c==0) ans++;
if(a%d==0) ans++;
if(a%(c*d)==0) ans--;
//cout<
D - Megalomania
Time Limit: 2 sec / Memory Limit: 1024 MB
Score: 400400 points
Problem Statement
Kizahashi, who was appointed as the administrator of ABC at National Problem Workshop in the Kingdom of AtCoder, got too excited and took on too many jobs.
Let the current time be time 00. Kizahashi has NN jobs numbered 11 to NN.
It takes AiAi units of time for Kizahashi to complete Job ii. The deadline for Job ii is time BiBi, and he must complete the job before or at this time.
Kizahashi cannot work on two or more jobs simultaneously, but when he completes a job, he can start working on another immediately.
Can Kizahashi complete all the jobs in time? If he can, print Yes; if he cannot, print No.
Constraints
- All values in input are integers.
- 1≤N≤2×1051≤N≤2×105
- 1≤Ai,Bi≤109(1≤i≤N)1≤Ai,Bi≤109(1≤i≤N)
Input
Input is given from Standard Input in the following format:
NN
A1A1 B1B1
..
..
..
ANAN BNBN
Output
If Kizahashi can complete all the jobs in time, print Yes; if he cannot, print No.
Sample Input 1 Copy
Copy
5
2 4
1 9
1 8
4 9
3 12
Sample Output 1 Copy
Copy
Yes
He can complete all the jobs in time by, for example, doing them in the following order:
- Do Job 22 from time 00 to 11.
- Do Job 11 from time 11 to 33.
- Do Job 44 from time 33 to 77.
- Do Job 33 from time 77 to 88.
- Do Job 55 from time 88 to 1111.
Note that it is fine to complete Job 33 exactly at the deadline, time 88.
Sample Input 2 Copy
Copy
3
334 1000
334 1000
334 1000
Sample Output 2 Copy
Copy
No
He cannot complete all the jobs in time, no matter what order he does them in.
Sample Input 3 Copy
Copy
30
384 8895
1725 9791
170 1024
4 11105
2 6
578 1815
702 3352
143 5141
1420 6980
24 1602
849 999
76 7586
85 5570
444 4991
719 11090
470 10708
1137 4547
455 9003
110 9901
15 8578
368 3692
104 1286
3 4
366 12143
7 6649
610 2374
152 7324
4 7042
292 11386
334 5720
Sample Output 3 Copy
Copy
Yes水
#include
using namespace std;
typedef long long LL;
const int N=200005;
//int a[N];
int n,L ;
struct node
{
int id;
int A,B;
}a[N];
bool cmp(node x,node y)
{
if(x.B==y.B)
return x.A>n;
for(int i=1;i<=n;i++)
{
cin>>a[i].A>>a[i].B;
a[i].id=i;
}
sort(a+1,a+n+1,cmp);
int t=0;
for(int i=1;i<=n;i++)
{
// cout<
E - Friendships
Time Limit: 2 sec / Memory Limit: 1024 MB
Score: 500500 points
Problem Statement
Does there exist an undirected graph with NN vertices satisfying the following conditions?
- The graph is simple and connected.
- The vertices are numbered 1,2,...,N1,2,...,N.
- Let MM be the number of edges in the graph. The edges are numbered 1,2,...,M1,2,...,M, the length of each edge is 11, and Edge ii connects Vertex uiui and Vertex vivi.
- There are exactly KK pairs of vertices (i, j) (i
If there exists such a graph, construct an example.
Constraints
- All values in input are integers.
- 2≤N≤1002≤N≤100
- 0≤K≤N(N−1)20≤K≤N(N−1)2
Input
Input is given from Standard Input in the following format:
NN KK
Output
If there does not exist an undirected graph with NN vertices satisfying the conditions, print -1.
If there exists such a graph, print an example in the following format (refer to Problem Statement for what the symbols stand for):
MM
u1u1 v1v1
::
uMuM vMvM
If there exist multiple graphs satisfying the conditions, any of them will be accepted.
Sample Input 1 Copy
Copy
5 3
Sample Output 1 Copy
Copy
5
4 3
1 2
3 1
4 5
2 3
This graph has three pairs of vertices such that the shortest distance between them is 22: (1, 4)(1, 4), (2, 4)(2, 4), and (3, 5)(3, 5). Thus, the condition is satisfied.
Sample Input 2 Copy
Copy
5 8
Sample Output 2 Copy
Copy
-1
There is no graph satisfying the conditions.
题意:
给你n与k,要求构造n个点,恰有k条距离为2 的路径的图
分析:
我们选取一个点当作中间节点,假设n=5
注意最多有3+2+1(即最多就有(n-2)*(n-1)/2)
连上一条你变会消除一条,模拟一下思路即可
接下来给出徐老爷的代码
#include
using namespace std;
typedef long long LL;
const int maxn=200+10;
int vis[maxn][maxn];
struct Node
{
int x,y;
Node(){}
Node(int a,int b):x(a),y(b){}
};
vectorG;
int main()
{
int n,k;
scanf("%d%d",&n,&k);
if(n==0)
{
printf("-1\n");
return 0;
}
int m=n-1;
int sum=(m)*(m-1)/2;
if(k>sum)
{
printf("-1\n");
return 0;
}
for(int i=1;i<=m;i++)
{
G.push_back(Node(i,n));
}
int i=1,j=2;
while(sum!=k)
{
sum--;
G.push_back(Node(i,j));
j++;
if(j==m+1) i++,j=i+1;
}
printf("%d\n",G.size());
for(int i=0;i F - Must Be Rectangular!
Time Limit: 2 sec / Memory Limit: 1024 MB
Score : 600600 points
Problem Statement
There are NN dots in a two-dimensional plane. The coordinates of the ii-th dot are (xi,yi)(xi,yi).
We will repeat the following operation as long as possible:
- Choose four integers aa, bb, cc, dd (a≠c,b≠d)(a≠c,b≠d) such that there are dots at exactly three of the positions (a,b)(a,b), (a,d)(a,d), (c,b)(c,b) and (c,d)(c,d), and add a dot at the remaining position.
We can prove that we can only do this operation a finite number of times. Find the maximum number of times we can do the operation.
Constraints
- 1≤N≤1051≤N≤105
- 1≤xi,yi≤1051≤xi,yi≤105
- If i≠ji≠j, xi≠xjxi≠xj or yi≠yjyi≠yj.
- All values in input are integers.
Input
Input is given from Standard Input in the following format:
NN
x1x1 y1y1
::
xNxN yNyN
Output
Print the maximum number of times we can do the operation.
Sample Input 1 Copy
Copy
3
1 1
5 1
5 5
Sample Output 1 Copy
Copy
1
By choosing a=1a=1, b=1b=1, c=5c=5, d=5d=5, we can add a dot at (1,5)(1,5). We cannot do the operation any more, so the maximum number of operations is 11.
Sample Input 2 Copy
Copy
2
10 10
20 20
Sample Output 2 Copy
Copy
0
There are only two dots, so we cannot do the operation at all.
Sample Input 3 Copy
Copy
9
1 1
2 1
3 1
4 1
5 1
1 2
1 3
1 4
1 5
Sample Output 3 Copy
Copy
16
We can do the operation for all choices of the form a=1a=1, b=1b=1, c=ic=i, d=jd=j (2≤i,j≤5)(2≤i,j≤5), and no more. Thus, the maximum number of operations is 1616.
题意:
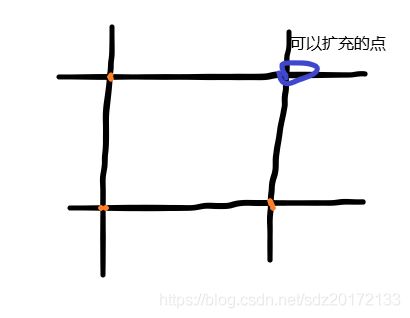
给你n个点,如果有三个点如下图红点所示,则蓝色的就是可以扩充的点,问有多少个这样的点。
分析:
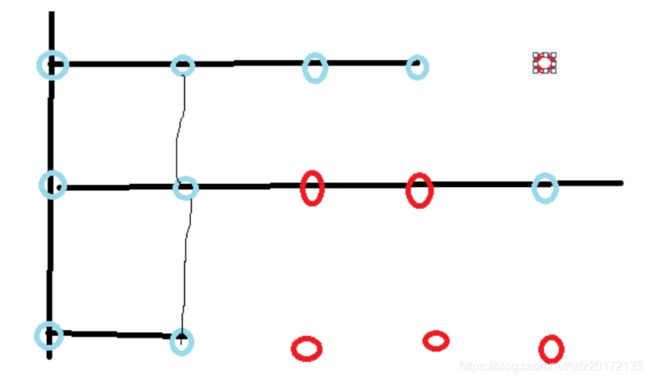
下图来自https://blog.csdn.net/mxYlulu/article/details/93769712
我们发现这个连通区域内的点数就是平行与x线条个数乘以平行与y线条个数,如果我们求出来这个,则减去已有的即可。
首先,连通区域的定义是x坐标与y坐标任意一点在这个集合内,这时候可以用并查集,但我们又不能完全的混合在一起,因为最后需要x的线条乘以y的线条个数,所以规定x在0~N,y在N+1~2*N(N为坐标最大值)
举一个例子,
N=4
(2,1)(1,1) (1,2)
则x坐标 1 2 3 4 y:5 6 7 8
fa 1 2 3 4 5 6 7 8
1.
添加(2,1)fa[find(x)]=find(y+N) fa[2]=5
x坐标 1 2 3 4 y:5 6 7 8
fa 1 5 3 4 5 6 7 8
2.
添加(1,1)fa[find(x)]=find(y+N) fa[1]=5
x坐标 1 2 3 4 y:5 6 7 8
fa 5 5 3 4 5 6 7 8
3.
添加(1,2)fa[find(x)]=find(y+N) fa[5]=6
x坐标 1 2 3 4 y:5 6 7 8
fa 5 5 3 4 6 6 7 8
#include
using namespace std;
#define N 100100
typedef long long ll;
int n,f[N<<1];
int getf(int x)
{
return x==f[x]?x:f[x]=getf(f[x]);
}
int sz1[N<<1],sz2[N<<1];
int main()
{
ll ans=0;
cin>>n;
for(int i=1; i>u>>v;
f[getf(u)]=getf(v+N);
}
for(int i=1; i<=N; ++i)
sz1[getf(i)]+=1;
for(int i=N+1; i