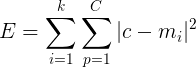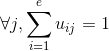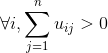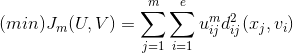四种聚类方法浅谈

       聚类作为一种重要的人类行为，早在还提时代，一个人就通过不断的改进下意识中的聚类模式类学会如何区分家猫、家狗等等动植物。目前，聚类方法也在许多领域都得到了广泛的研究和成功应用。常见的如：模式识别、数据分析、图像处理、市场研究以及文档分析等。

  聚类原理：聚类就是按照某个特定的标准（最常见的如距离）把一个数据集分割成不同的类或者簇，从而使得同一个簇类的数据对象的相似性尽可能的最大，同时不同簇中的数据对象之间的差异尽可能的最大。

1.聚类算法的分类

       目前，有着大量的聚类算法[3]。但对于具体的应用，聚类算法的选择要根据数据类型以及聚类的目的进行适当的选择。如果聚类分析被用作描述或者探查的工具，可以对too那样的数据尝试多种算法，以发现数据可能揭示的结果。

  聚类算法主要可以划分为如下几类：划分方法、层次方法、基于密度的方法、基于网络的方法以及基于模型的方法[4-6]。

       每一类中都存在着得到广泛应用的方法。如：划分法中的k-means[7]聚类方法、层次聚类方法中凝聚性层次聚类方法、基于模型方法中的神经网络聚类方法等。

       目前，聚类问题的研究不仅仅局限于上述的硬聚类，即每一个数据只能被归为一类，模糊聚类[10]也是聚类分析中研究较为广发的一个分支。模糊聚类通过隶属函数来确定每个数据隶属于各个簇的程度，而不是讲一个数据对象硬性的归为某一个簇中。目前已经有很多关于模糊聚类的算法被提出。最著名的就是FCM算法。

       下面将主要对k-means聚类算法、凝聚型层次聚类方法、神经网络聚类方法之SOM和模型聚类的FCM算法通过通用测试数据及进行聚类效果的比较和分析。

2.四种聚类方法

2.1 k-means

       k-means是划分方法中较经典的聚类方法之一。由于该算法的效率高，所以在对大规模数据进行聚类的时候被广泛使用。目前许多算法都是围绕该算法进行扩展和改进的。k-means算法以k为参数，把n个对象分为k个簇，使簇内具有较高的相似度，簇间具有较低的相似度。k-means算法的处理过程如下：

     （1）随机的选取k个对象，每个对象初始的代表了一个簇的平均值或中心；

     （2）对剩余的每个对象，根据其与各个簇中心的距离，将他赋给最近的簇；

     （3）然后重新计算每个簇的平均值；

     （4）如此不断重复，直到准则函数收敛或者达到设定的迭代次数

       通常采用的准则函数为：

                                                                                 

       上式中E为数据中所有对象与簇中心的平方误差总和，p表示空间中的一个点，mi表示一个簇中心的坐标，k为簇的个数。

2.2 层次聚类算法

       根据层次分解的顺序是自底向上还是自上向下的，层次聚类算法分为聚类的层次算法和分裂的层次聚类算法。凝聚型层次聚类的策略是先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，知道所有的对象都在一个簇中，或者某个终结条件被满足。绝大多数层次聚类数据凝聚型层次聚类方法，他们只是在簇之间相似度的定义上有一定的不同。四种广发采用的簇间距离度量方法如下：

     （1）最小距离    ：

                                                                            

     （2） 最大距离    ：

                                                                           

     （3）平均值距离 ：

                                                                           

     （4）平均距离     ：

                                                                           

        注：mi、mj表示簇的中心

       这里给出采用最小距离的凝聚型层次聚类算法计算步骤：

     （1）将每个对象看为一个类，计算两两之间的最小距离；

     （2）将距离最小的两个类合并为一个新的类；

     （3）重复计算新类和所有类别之间的距离；

     （4）重复过程（2）和过程（3）知道所有类别合并为一个类或者迭代结束。

2.3 SOM聚类方法

       SOM 神经网络[11]是由芬兰神经网络专家 Kohonen 教授提出的，该算法假设在输入对象中 存在一些拓扑结构或顺序，可以实现从输入空间(n 维)到输出平面(2 维)的降维映射，其映射具 有拓扑特征保持性质,与实际的大脑处理有很强的理论联系。

       SOM 网络包含输入层和输出层。输入层对应一个高维的输入向量，输出层由一系列组织在 2 维网格上的有序节点构成，输入节点与输出节点通过权重向量连接。 学习过程中，找到与 之距离最短的输出层单元，即获胜单元，对其更新。同时，将邻近区域的权值更新，使输出节 点保持输入向量的拓扑特征。

       SOM算法过程如下：

       (1) 网络初始化，对输出层每个节点权重赋初值；

       (2) 将输入样本中随机选取输入向量，找到与输入向量距离最小的权重向量；

       (3) 定义获胜单元，在获胜单元的邻近区域调整权重使其向输入向量靠拢；

       (4) 提供新样本、进行训练；

       (5) 收缩邻域半径、减小学习率、重复，直到小于允许值，输出聚类结果。

2.4 FCM聚类算法

       1965 年美国加州大学柏克莱分校的扎德教授第一次提出了‘集合’的概念。经过十多年的发展， 模糊集合理论渐渐被应用到各个实际应用方面。为克服非此即彼的分类缺点，出现了以模糊集 合论为数学基础的聚类分析。用模糊数学的方法进行聚类分析，就是模糊聚类分析[12]。

       FCM 算法是一种以隶属度来确定每个数据点属于某个聚类程度的算法。该聚类算法是传 统硬聚类算法的一种改进。

       FCM原理如下：

       设数据集,他的模糊c划分可用模糊矩阵表示，矩阵的元素表示第j个数据点属于第i个类的隶属度，满足如下条件：

                                                                               

                                                                               

                                                                               

       目前被广泛使用的聚类准则为取聚类加权平均误差平方和的极小值，即：

                                                             

       式中V表示聚类中心，m表示加权指数。

                                                                         

       算法的流程如下：

（1）建立标准化数据矩阵；

（2）建立模糊相似矩阵，初始化隶属度矩阵；

（3）算法开发迭代，直到目标函数收敛到极小值；

（4）根据迭代结果，由最后的隶属度矩阵确定数据所属的类，显示最后的聚类结果。

       以上略改自“深度学习500问”！！！，如有问题请指出。