用数组模拟栈+单调栈的几个例子(leetcode)
数组模拟栈和队列
在c++中,stl中栈的常见操作为入栈、出栈、判断栈是否为空、返回栈的长度等,以下我们就用数组来模拟栈的常见操作。note:在实际算法题中行,用stl中的栈往往不如用数组模拟的快。
#include
using namespace std;
const int N=1000010;
int stk[N];
int tt;
在这里我们创建了一个长度为N的数组stk,用tt来表示栈顶元素的索引,默认开始将tt设为0。
1.入栈
stk[++tt]=x;
2.出栈
tt--;
3.判断栈是否为空
if(tt) not empty;
else empty;
4.拿出栈顶元素
stk[tt];
以上就为用数组模拟栈的几个简单操作。
单调栈
单调栈的定义:单调栈就是栈内元素单调递增或者单调递减的栈,单调栈只能在栈顶操作。
例如:我们借用拿号排队的场景来说明下。现在有很多人在排队买可乐,每个人手里都拿着号,越靠前的人手里的号越小,但是号不一定是连续的。小明拿了号后并没有去排队,而是跑去约会了。等他回来后,发现队伍已经排得很长了,他不能直接插入到队伍里,不然人家以为他是来插队的。小明只能跑到队伍最后,挨个询问排队人手里的号,小明认为号比他大的人都是“插队”的,于是小明就会施魔法把这些人变消失,直到小明找到号比他小的为止。在上面这个场景里,大家排的队伍就像是单调栈,因为大家手里拿的号是单调递增的。而小明找自己位置的这个过程就是元素加入单调栈的过程。新加入的元素如果加到栈顶后,如果栈里的元素不再是单调递增了,那么我们就删除加入前的栈顶元素,就像小明施魔法把“插队”的人变消失一样。直到新元素加入后,栈依然是单调递增时,我们才把元素加进栈里。
单调栈的维护是 O(n) 级的时间复杂度,因为所有元素只会进入栈一次,并且出栈后再也不会进栈了。
单调栈的性质:
1.单调栈里的元素具有单调性
2.元素加入栈前,会在栈顶端把破坏栈单调性的元素都删除
3.使用单调栈可以找到元素向左遍历第一个比他小的元素,也可以找到元素向左遍历第一个比他大的元素。
单调栈的主要应用场景就是性质3以及根据性质3抽象出来的各种问题,以下为几个经典问题。
例1: 单调递增栈
给定一个长度为N的整数数列,输出每个数左边第一个比它小的数,如果不存在则输出-1。
输入格式:
第一行包含整数N,表示数列长度。
第二行包含N个整数,表示整数数列。
输出格式
共一行,包含N个整数,其中第i个数表示第i个数的左边第一个比它小的数,如果不存在则输出-1。
数据范围
1≤N≤105
1≤数列中元素≤109
输入样例:
5
3 4 2 7 5
输出样例:
-1 3 -1 2 2
代码:
#include
using namespace std;
const int N=100010;
int stk[N],tt;
int main(){
int n;
scanf("%d",&n);
for (int i=0;i=x) tt--; //只要栈不空,且将要插入的元素破坏了原有的单调性,则调整栈顶元素
if(tt) cout< 同理:单调递减栈,可以找到左起第一个比自己大的数字,代码如下:
#include
using namespace std;
const int N=100010;
int stk[N],tt;
int main(){
int n;
scanf("%d",&n);
for (int i=0;i 这里有个思想的转换,单调栈中不一定要存元素的值,也可以存元素的索引,比如存水题中的while( tt && height[stk[tt]]
例2:问题抽象后的装水问题(leetcode42:trapping rain water)
题目描述
给定n个非负整数,代表一个高度地图,每个位置的矩形条宽度为1,计算该图形能装下多少单位的水。
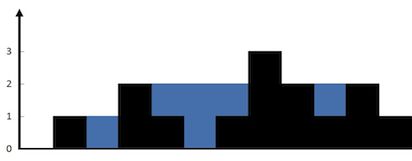
可以从两个方面考虑。
方法一:每个格子放水的高度是由其左边的最大高度和右边的最大高度来决定的,如图:

按照这样的思路,从左往右扫描一遍,得出每个元素左边的最大值,放入一个vector中,从右往左再扫描一遍,得出每个元素右边的最大值,放入另外一个vector中,最后对每个元素计算一遍高度:
height[i]=max(0,min(left_max[i],right_max[i])-height[i]) 最后将其全部累加即可。
时间复杂度分析:
都是线性扫描,故只需要O(n)的时间,扫描了3次,全部时间复杂度为3n
代码:
class Solution {
public:
int trap(vector& height) {
int n=height.size();
if (n == 0) return 0;
vector left_max(n),right_max(n),acre(n);
left_max[0]=height[0],right_max[n-1]=height[n-1];
for (int i=0;i0;i--){
right_max[i-1]=max(right_max[i],height[i]);
}
int ans=0;
for (int i=0;i
方法二:用单调栈的思想,若想能放水,必须需要形成一个凹槽,形成一个凹槽就需要三个元素,一个为底,两个为两边的墙,这个时候我们维护一个单调递减栈,若遇到一个比栈顶高度还高的元素i时,i就为栈顶元素右边的第一个比自己高的元素,则可做为自己的右边的墙,若栈中至少有两个元素,则栈顶为底部,栈左边的第一个元素就为左边的墙,这时便形成了一个凹槽。
这个是自己通俗的理解,这里转载大神的专业讲解:
1.换一种思路,考虑每个位置左边和右边第一个比它高的位置的矩形条,以及三个矩形条构成的U型。
2.维护单调递减的单调栈,在每次出栈时,i即为当前栈顶st.top()位置第一个比它高的矩形的位置,弹出栈顶,并将当前栈顶记为top。
3.假设此时栈中仍然存在矩形,现在st.top()、top与i三个位置构成一个U型,其中top位置代表U型的底部,此时可以计算出该U型所能接受的水的面积为
(i−st.top()−1)∗(min(height[st.top()],height[i])−height[top])
如果想不清楚,建议根据代码在纸上模拟一下数据[3, 0, 0, 1, 0, 2, 0, 4],这个例子中总共会出现五次U型。
代码如下:
class Solution {
public:
int trap(vector& height){
int n=height.size();
if(n < 2)
return 0;
int stk[n+1];
int tt=0,res=0;
for (int i=0;i
stl版的代码如下:
class Solution {
public:
int trap(vector& height) {
int n = height.size(), ans = 0;
stack st;
for (int i = 0; i < n; i++) {
while (!st.empty() && height[st.top()] < height[i]) {
int top = st.top();
st.pop();
if (st.empty()) break;
ans += (i - st.top() - 1) * (min(height[st.top()], height[i]) - height[top]);
}
st.push(i);
}
return ans;
}
};
自己感觉回答的很好的一条:
对于单调栈的第三条性质,你可能会产生疑问,为什么使用单调栈可以找到元素向左遍历第一个比他大的元素,而不是最后一个比他大的元素呢?
我们可以从单调栈中元素的单调性来解释这个问题,由于单调栈中的元素只能是单调递增或者是单调
递减的,所以我们可以分别讨论这两种情况(假设不存在两个相同的元素):
1.当单调栈中的元素是单调递增的时候,根据上面我们从数组的角度阐述单调栈的性质的叙述,可以得出:
(1).当a > b 时,则将元素a插入栈顶,新的栈顶则为a
(2).当a < b 时,则将从当前栈顶位置向前查找(边查找,栈顶元素边出栈),直到找到第一个比a小的数,停止查找,将元素a
插入栈顶(在当前找到的数之后,即此时元素a找到了自己的“位置”)
2.当单调栈中的元素是单调递减的时候,则有:
(1).当a < b 时,则将元素a插入栈顶,新的栈顶则为a
(2).当a > b 时,则将从当前栈顶位置向前查找(边查找,栈顶元素边出栈),直到找到第一个比a大的数,停止查找,将元素a
插入栈顶(在当前找到的数之后,即此时元素a找到了自己的“位置”)
谢谢您的观看! (一只算法小白跟您一起加油)
参考链接:https://blog.csdn.net/liujian20150808/article/details/50752861
例2:问题抽象后的装水问题(leetcode42:trapping rain water)
题目描述
给定n个非负整数,代表一个高度地图,每个位置的矩形条宽度为1,计算该图形能装下多少单位的水。

可以从两个方面考虑。
方法一:每个格子放水的高度是由其左边的最大高度和右边的最大高度来决定的,如图:

按照这样的思路,从左往右扫描一遍,得出每个元素左边的最大值,放入一个vector中,从右往左再扫描一遍,得出每个元素右边的最大值,放入另外一个vector中,最后对每个元素计算一遍高度:
height[i]=max(0,min(left_max[i],right_max[i])-height[i]) 最后将其全部累加即可。
时间复杂度分析:
都是线性扫描,故只需要O(n)的时间,扫描了3次,全部时间复杂度为3n
代码:
class Solution {
public:
int trap(vector& height) {
int n=height.size();
if (n == 0) return 0;
vector left_max(n),right_max(n),acre(n);
left_max[0]=height[0],right_max[n-1]=height[n-1];
for (int i=0;i0;i--){
right_max[i-1]=max(right_max[i],height[i]);
}
int ans=0;
for (int i=0;i 方法二:用单调栈的思想,若想能放水,必须需要形成一个凹槽,形成一个凹槽就需要三个元素,一个为底,两个为两边的墙,这个时候我们维护一个单调递减栈,若遇到一个比栈顶高度还高的元素i时,i就为栈顶元素右边的第一个比自己高的元素,则可做为自己的右边的墙,若栈中至少有两个元素,则栈顶为底部,栈左边的第一个元素就为左边的墙,这时便形成了一个凹槽。
这个是自己通俗的理解,这里转载大神的专业讲解:
1.换一种思路,考虑每个位置左边和右边第一个比它高的位置的矩形条,以及三个矩形条构成的U型。
2.维护单调递减的单调栈,在每次出栈时,i即为当前栈顶st.top()位置第一个比它高的矩形的位置,弹出栈顶,并将当前栈顶记为top。
3.假设此时栈中仍然存在矩形,现在st.top()、top与i三个位置构成一个U型,其中top位置代表U型的底部,此时可以计算出该U型所能接受的水的面积为
(i−st.top()−1)∗(min(height[st.top()],height[i])−height[top])
如果想不清楚,建议根据代码在纸上模拟一下数据[3, 0, 0, 1, 0, 2, 0, 4],这个例子中总共会出现五次U型。
代码如下:
class Solution {
public:
int trap(vector& height){
int n=height.size();
if(n < 2)
return 0;
int stk[n+1];
int tt=0,res=0;
for (int i=0;i stl版的代码如下:
class Solution {
public:
int trap(vector& height) {
int n = height.size(), ans = 0;
stack st;
for (int i = 0; i < n; i++) {
while (!st.empty() && height[st.top()] < height[i]) {
int top = st.top();
st.pop();
if (st.empty()) break;
ans += (i - st.top() - 1) * (min(height[st.top()], height[i]) - height[top]);
}
st.push(i);
}
return ans;
}
};
自己感觉回答的很好的一条:
对于单调栈的第三条性质,你可能会产生疑问,为什么使用单调栈可以找到元素向左遍历第一个比他大的元素,而不是最后一个比他大的元素呢?
我们可以从单调栈中元素的单调性来解释这个问题,由于单调栈中的元素只能是单调递增或者是单调
递减的,所以我们可以分别讨论这两种情况(假设不存在两个相同的元素):
1.当单调栈中的元素是单调递增的时候,根据上面我们从数组的角度阐述单调栈的性质的叙述,可以得出:
(1).当a > b 时,则将元素a插入栈顶,新的栈顶则为a
(2).当a < b 时,则将从当前栈顶位置向前查找(边查找,栈顶元素边出栈),直到找到第一个比a小的数,停止查找,将元素a
插入栈顶(在当前找到的数之后,即此时元素a找到了自己的“位置”)
2.当单调栈中的元素是单调递减的时候,则有:
(1).当a < b 时,则将元素a插入栈顶,新的栈顶则为a
(2).当a > b 时,则将从当前栈顶位置向前查找(边查找,栈顶元素边出栈),直到找到第一个比a大的数,停止查找,将元素a
插入栈顶(在当前找到的数之后,即此时元素a找到了自己的“位置”)
谢谢您的观看! (一只算法小白跟您一起加油)
参考链接:https://blog.csdn.net/liujian20150808/article/details/50752861