数据结构 学习总结3 栈

栈：
限定只能在表的一端进行插入和删除运算的线性表（只能在栈顶操作）

逻辑结构与同线性表相同，仍为一对一关系
存储结构 用顺序栈或链栈存储均可，但以顺序栈更常见

只能在栈顶(表尾)运算，且访问结点时依照后进先出（LIFO）或先进后出（FILO）的原则

关键是编写入栈和出栈函数，具体实现依顺序栈或链栈的不同而不同。
基本操作有入栈、出栈、读栈顶元素值、建栈、或判断栈满、栈空等。

堆栈是什么？它与一般线性表有什么不同
堆栈是一种特殊的线性表，它只能在表的一端（即栈顶）进行插入和删除运算。
与一般线性表的区别：仅在于运算规则不同。

一般线性表 堆栈
逻辑结构：一对一 逻辑结构：一对一
存储结构：顺序表、链表 存储结构：顺序栈、链栈
运算规则：随机存取 运算规则：后进先出(LIFO)

栈 是仅在表尾进行插入、删除操作的线性表。
表尾(即 an 端)称为栈顶 top ; 表头(即 a1 端)称为栈底base

插入元素到栈顶（即表尾）的操作，称为入栈。
从栈顶（即表尾）删除最后一个元素的操作，称为出栈。

强调：插入和删除都只能在表的一端（栈顶）进行！

顺序栈

栈的顺序存储表示

#define  MAXSIZE      100;
typedef  struct {
   SElemType   *base;
   SElemType   *top;
   int            stacksize;
}SqStack;

顺序栈中的PUSH函数

status Push(ElemType x) 
{ if(top>M){上溢}
  else v[top++]=x;
}

顺序栈中的POP函数

status Pop( )
{ if(top=L) { 下溢 }
  else 
   { y=v[--top];       
     return(y);
   } 
 }

一个栈的输入序列是12345，若在入栈的过程中允许出栈，则栈的输出序列43512可能实现吗？12345的输出呢？
43512不可能实现，主要是其中的12顺序不能实现；
12345的输出可以实现，只需压入一个立即弹出一个即可。

如果一个栈的输入序列为123456，能否得到435612和135426的出栈序列？
435612中到了12顺序不能实现；
135426可以实现。

一个栈的输入序列为123，若在入栈的过程中允许出栈，则可能得到的出栈序列是什么？

可以通过穷举所有可能性来求解：
① 1入1出， 2入2出，3入3出， 即123；
② 1入1出， 2、3入3、2出， 即132；
③ 1、2入，2出， 3入3出， 即231；
④ 1、2入，2、1出，3入3出， 即213；
⑤ 1、2、3入，3、2、1出， 即321；
合计有5种可能性。

若入栈动作使地址向高端增长，称为“向上生成”的栈；
若入栈动作使地址向低端增长，称为“向下生成”的栈；
对于向上生成的栈
入栈口诀：栈指针top先压后加（v[top++]=x）；
出栈口诀：栈指针top先减后弹（y=v[–top]) 。

栈不存在的条件： base=NULL;
栈为空 的条件 ： base=top;
栈满的条件 ： top-base=stacksize;
栈指针top始终指向栈顶元素的上一个位置

说明
① 链栈不必设头结点，因为栈顶（表头）操作频繁；
②采用链栈存储方式，可使多个栈共享空间；当栈中元素个数变化较大，且存在多个栈的情况下，链栈是栈的首选存储方式。

表达式求值

( 这是栈应用的典型例子 )
这里，表达式求值的算法是 “算符优先法”
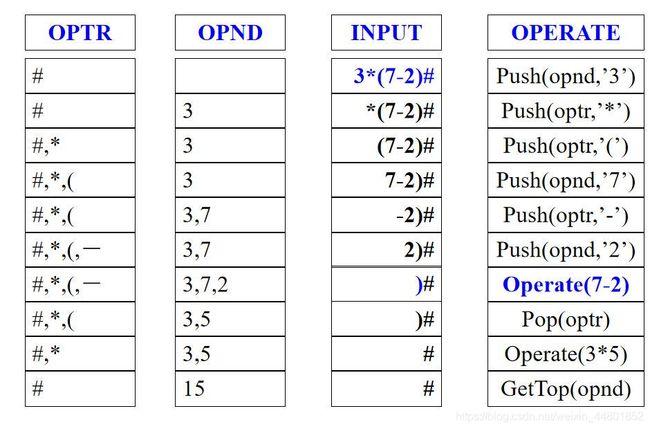
例如：3*（7 – 2 ）
（1）要正确求值，首先了解算术四则运算的规则：
a. 从左算到右
b. 先乘除，后加减
c. 先括号内，后括号外
由此，此表达式的计算顺序为：
3*（7 – 2 ）= 3 * 5 = 15
（2）根据上述三条运算规则，在运算的每一步中，对任意相继出现的算符01和02 ，都要比较优先权关系。
算符优先法所依据的算符间的优先关系见教材P53表3.1
（是提供给计算机用的表！）
由表可看出，右括号 ) 和井号 # 作为02时级别最低；

由c 规则得出： * ，/， + ，-为01时的优先权低于‘（’，高于‘）’
由a规则得出：‘（’=‘）’ 表明括号内运算，已算完。
‘ # ’=‘ # ’ 表明表达式求值完毕。

（3）算法思想：
设定两栈：操作符栈 OPTR ，操作数栈 OPND
栈初始化：设操作数栈 OPND 为空；操作符栈 OPTR 的栈底元素为表达式起始符 ‘#’；
依次读入字符：是操作数则入OPND栈，是操作符则要判断：
if 栈顶元素 > 操作符 ，则退栈、计算，结果压入OPND栈；
栈顶元素 =操作符且不为‘#’，脱括号（弹出左括号）；
栈顶元素<操作符 ，压入OPTR栈。

Status    EvaluateExpression( OperandType  &result)   {
  InitStack(OPND); InitStack(OPTR);Push(OPTR ,’#’);c=getchar();
    while((c!=‘#’)&&(GetTop(OPTR)!=‘#’))
   {  if (!In(c,OP)  {    Push(OPND,c);   c=getchar();}  
       else   switch(compare(c,GetTop(OPTR)))
                 {case ‘>’ :    Push(OPTR , c); c=getchar();break; 
                   case ‘=’:   Pop(OPTR);c=getchar();break;
                  case ‘<’ : temat=Pop(OPTR); b=Pop();a=Pop();
                                  result= Operate(a,temat,b);Push(OPND,result);
                                  c=getchar();break;  
                } //switch  }//while   
    result=GetTop(OPND);}//EvaluateExpression

栈与递归

在函数执行中，直接或间接调用自己的函数称为递归函数。
常见的递归方法有两种
直接递归

间接递归

递归的定义
若一个对象部分地包含它自己, 或用它自己给自己定义, 则称这个对象是递归的；
若一个过程直接地或间接地调用自己, 则称这个过程是递归的过程。
以下三种情况常常用到递归方法
递归定义的数学函数
具有递归特性的数据结构
可递归求解的问题

例 求ｎ！。
n! = n X n-1 X n-2 X 1;

int jiecheng（int ｎ）        ／*求n的阶乘*／
 {  int i，result = 1；
    for （i=1；i<=n；i++）
         result = result * i;
    return result；
｝

int jiecheng（int ｎ）        ／*求n的阶乘*／
 {  int result;
       if (n==1) || (n == 0)     
          return 1;
       else
          return (n * jiecheng(n-1));
｝

具有递归特性的数据结构
树和广义表
用分治法求解递归问题
分治法
对于一个较为复杂的问题，能够分解成几个相对简单的且解法相同或类似的子问题来求解
必备的三个条件
能将一个问题转变成一个新问题，而新问题与原问题的解法相同或类同，不同的仅是处理的对象，且这些处理对象是变化有规律的
可以通过上述转化而使问题简化
必须有一个明确的递归出口，或称递归的边界

汉诺塔

#include
int c=0;       // 定义一个全局变量，记录搬动步数
void move(char, int, char);     // 函数声明，仅使用数据类型的方式，移动一个盘子的操作
void hanoi(int, char , char, char);    // 函数声明，汉诺塔的解决办法
int main()
{
       hanoi(4,‘a’, ‘b’, ‘c’);      // 移动4个盘子，柱子名称分别为 a    b   c
}

void move(char x, int n, char z)   // 参数含义：将第n个盘子从x柱子移到z柱子
{
    printf(“第%d 步:移动盘子 %d 从 %c 到 %c\n",++c, n, x, z);
}
void hanoi(int n, char x, char y, char z)  // 将n个盘子从x柱子借助y柱子移到z柱子
{
       if ( n == 1 )
            move(x,1,z);
       else
     {     hanoi(n-1, x, z, y);
            move(x,n,z);
            hanoi(n-1, y, x, z);
     }

64片金片移动次数：2^64-1=18446744073709551615
假如每秒钟一次，共需多长时间呢？
一年大约有31536926秒，移完这些金片需要５８００多亿年
世界、梵塔、庙宇和众生都已经灰飞烟灭 ……