无人驾驶技术——无损卡尔曼滤波(UKF)
文章目录
- 无损卡尔曼滤波(UKF)
- UKF Predict
- 1.选择预测点sigma点
- sigma点计算代码实现
- 添加过程噪声处理
- 构建噪声扩充矩阵 c++
- 2.预测sigma点
- 预测sigma点方法
- 预测sigma点 c++代码实现
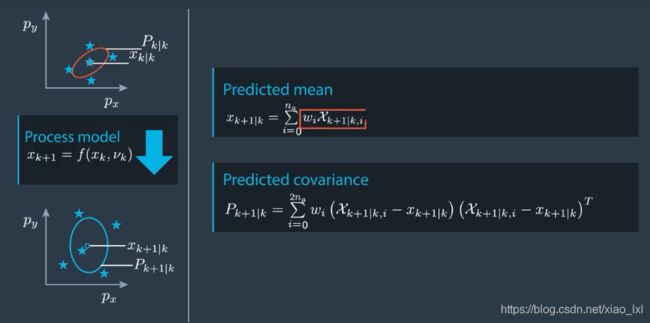
- 3.根据预测的sigma点预测状态均值和协方差矩阵
- 预测均值和协方差c++代码实现
- UKF Update
- 测量预测
- 测量预测c++代码实现
- Update之更新状态
- 更新状态c++代码实现
- 噪音参数和评估选择
- 如何选择噪音参数
- 直线加速度噪声参数直观
- 偏航加速度噪声参数直观
- 测量噪声参数
- 怎么评估选择
无人驾驶技术——无损卡尔曼滤波(UKF)
前面总结了卡尔曼滤波 【无人驾驶技术——初探Kalman滤波器(KF)】和
扩展卡尔曼滤波【无人驾驶技术——扩展Kalman滤波(EKF)】,
今天主要学习下无损卡尔曼滤波(UKF)
无损卡尔曼滤波(UKF)
无损卡尔曼滤波(UKF)是处理非线性过程模型或非线性测量模型的替代方案。但UKF不会对非线性函数进行线性化处理,它使用所谓的sigma点来近似概率分布。
它有两个好处:
- sigma点近似非线性转换的效果比线性化更好;
- 可以省去计算雅可比矩阵的过程。
无损卡尔曼滤波器不需要将非线性函数线性化;相反,无损卡尔曼滤波器从高斯分布中取代表点。这些点将被插入非线性方程。
无损卡尔曼滤波器随时间处理测量值的方式和扩展卡尔曼滤波器是一样的。它们都有预测步骤,这个步骤是独立于测量模型的,在这一步里,需要使用上一节学到的CTRV模型。接下来是更新步骤,我们使用雷达测量模型或激光测量模型。
对于UKF 和EKF,我们可以使用同样的顶层处理链,两者的不同之处是,UKF处理的是非线性过程模型或非线性测量模型的方法,它使用的方法叫无损变换。
UKF Predict
无损滤波预测步骤主要分为三步:
1.需要知道选择sigma点的好办法
2.需要知道如何预测sigma点
3.需要知道如何根据预测的sigma点计算预测、均值和协方差
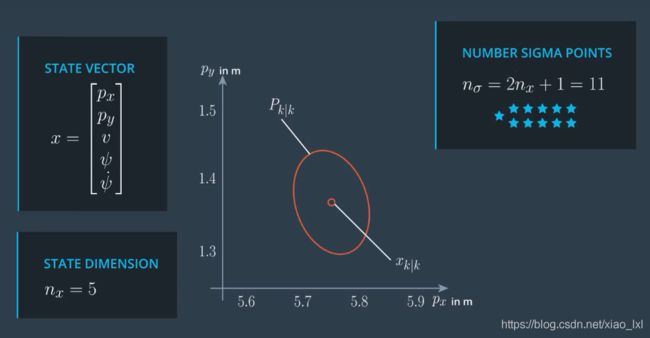
1.选择预测点sigma点

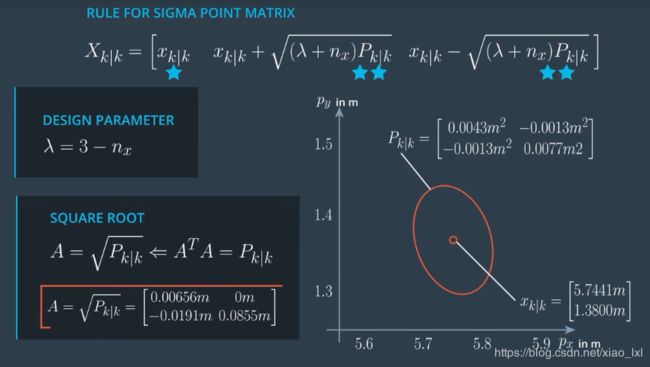
将下面各个值代入上面的sigma点矩阵后,计算结果如下:

可见,主要是根据以下公式求得sigma值:

sigma点计算代码实现
ukf.h
#ifndef UKF_H
#define UKF_H
#include "Dense"
class UKF {
public:
/**
* Constructor
*/
UKF();
/**
* Destructor
*/
virtual ~UKF();
/**
* Init Initializes Unscented Kalman filter
*/
void Init();
/**
* Student assignment functions
*/
void GenerateSigmaPoints(Eigen::MatrixXd* Xsig_out);
void AugmentedSigmaPoints(Eigen::MatrixXd* Xsig_out);
void SigmaPointPrediction(Eigen::MatrixXd* Xsig_out);
void PredictMeanAndCovariance(Eigen::VectorXd* x_pred,
Eigen::MatrixXd* P_pred);
void PredictRadarMeasurement(Eigen::VectorXd* z_out,
Eigen::MatrixXd* S_out);
void UpdateState(Eigen::VectorXd* x_out,
Eigen::MatrixXd* P_out);
};
#endif // UKF_H
ukf.cpp
#include "ukf.h"
#include
using Eigen::MatrixXd;
using Eigen::VectorXd;
UKF::UKF() {
Init();
}
UKF::~UKF() {
}
void UKF::Init() {
}
/**
* Programming assignment functions:
*/
void UKF::GenerateSigmaPoints(MatrixXd* Xsig_out) {
// set state dimension
int n_x = 5;
// define spreading parameter
double lambda = 3 - n_x;
// set example state
VectorXd x = VectorXd(n_x);
x << 5.7441,
1.3800,
2.2049,
0.5015,
0.3528;
// set example covariance matrix
MatrixXd P = MatrixXd(n_x, n_x);
P << 0.0043, -0.0013, 0.0030, -0.0022, -0.0020,
-0.0013, 0.0077, 0.0011, 0.0071, 0.0060,
0.0030, 0.0011, 0.0054, 0.0007, 0.0008,
-0.0022, 0.0071, 0.0007, 0.0098, 0.0100,
-0.0020, 0.0060, 0.0008, 0.0100, 0.0123;
// create sigma point matrix
MatrixXd Xsig = MatrixXd(n_x, 2 * n_x + 1);
// calculate square root of P
MatrixXd A = P.llt().matrixL();
/**
* Student part begin
*/
// your code goes here
// calculate sigma points ...
// set sigma points as columns of matrix Xsig
Xsig.col(0) = x;
// set remaining sigma points
for (int i = 0; i < n_x; ++i)
{
Xsig.col(i+1) = x + sqrt(lambda+n_x) * A.col(i);
Xsig.col(i+1+n_x) = x - sqrt(lambda+n_x) * A.col(i);
}
/**
* Student part end
*/
// print result
// std::cout << "Xsig = " << std::endl << Xsig << std::endl;
// write result
*Xsig_out = Xsig;
}
/**
* expected result:
* Xsig =
* 5.7441 5.85768 5.7441 5.7441 5.7441 5.7441 5.63052 5.7441 5.7441 5.7441 5.7441
* 1.38 1.34566 1.52806 1.38 1.38 1.38 1.41434 1.23194 1.38 1.38 1.38
* 2.2049 2.28414 2.24557 2.29582 2.2049 2.2049 2.12566 2.16423 2.11398 2.2049 2.2049
* 0.5015 0.44339 0.631886 0.516923 0.595227 0.5015 0.55961 0.371114 0.486077 0.407773 0.5015
* 0.3528 0.299973 0.462123 0.376339 0.48417 0.418721 0.405627 0.243477 0.329261 0.22143 0.286879
*/
main.cpp
#include
#include "Dense"
#include "ukf.h"
using Eigen::MatrixXd;
int main() {
// Create a UKF instance
UKF ukf;
/**
* Programming assignment calls
*/
MatrixXd Xsig = MatrixXd(5, 11);
ukf.GenerateSigmaPoints(&Xsig);
// print result
std::cout << "Xsig = " << std::endl << Xsig << std::endl;
return 0;
}
添加过程噪声处理
为什么需要添加噪声进行扩充?
因为过程噪声对状态有非线性影响。





构建噪声扩充矩阵 c++
ukf.h
#ifndef UKF_H
#define UKF_H
#include "Dense"
class UKF {
public:
/**
* Constructor
*/
UKF();
/**
* Destructor
*/
virtual ~UKF();
/**
* Init Initializes Unscented Kalman filter
*/
void Init();
/**
* Student assignment functions
*/
void GenerateSigmaPoints(Eigen::MatrixXd* Xsig_out);
void AugmentedSigmaPoints(Eigen::MatrixXd* Xsig_out);
void SigmaPointPrediction(Eigen::MatrixXd* Xsig_out);
void PredictMeanAndCovariance(Eigen::VectorXd* x_pred,
Eigen::MatrixXd* P_pred);
void PredictRadarMeasurement(Eigen::VectorXd* z_out,
Eigen::MatrixXd* S_out);
void UpdateState(Eigen::VectorXd* x_out,
Eigen::MatrixXd* P_out);
};
#endif // UKF_H
ukf.cpp
#include
#include "ukf.h"
using Eigen::MatrixXd;
using Eigen::VectorXd;
UKF::UKF() {
Init();
}
UKF::~UKF() {
}
void UKF::Init() {
}
/**
* Programming assignment functions:
*/
void UKF::AugmentedSigmaPoints(MatrixXd* Xsig_out) {
// set state dimension
int n_x = 5;
// set augmented dimension
int n_aug = 7;
// Process noise standard deviation longitudinal acceleration in m/s^2
double std_a = 0.2;
// Process noise standard deviation yaw acceleration in rad/s^2
double std_yawdd = 0.2;
// define spreading parameter
double lambda = 3 - n_aug;
// set example state
VectorXd x = VectorXd(n_x);
x << 5.7441,
1.3800,
2.2049,
0.5015,
0.3528;
// create example covariance matrix
MatrixXd P = MatrixXd(n_x, n_x);
P << 0.0043, -0.0013, 0.0030, -0.0022, -0.0020,
-0.0013, 0.0077, 0.0011, 0.0071, 0.0060,
0.0030, 0.0011, 0.0054, 0.0007, 0.0008,
-0.0022, 0.0071, 0.0007, 0.0098, 0.0100,
-0.0020, 0.0060, 0.0008, 0.0100, 0.0123;
// create augmented mean vector
VectorXd x_aug = VectorXd(7);
// create augmented state covariance
MatrixXd P_aug = MatrixXd(7, 7);
// create sigma point matrix
MatrixXd Xsig_aug = MatrixXd(n_aug, 2 * n_aug + 1);
/**
* Student part begin
*/
// create augmented mean state
x_aug.head(5) = x;
x_aug(5) = 0;
x_aug(6) = 0;
// create augmented covariance matrix
P_aug.fill(0.0);
P_aug.topLeftCorner(5,5) = P;
P_aug(5,5) = std_a*std_a;
P_aug(6,6) = std_yawdd*std_yawdd;
// create square root matrix
MatrixXd L = P_aug.llt().matrixL();
// create augmented sigma points
Xsig_aug.col(0) = x_aug;
for (int i = 0; i< n_aug; ++i) {
Xsig_aug.col(i+1) = x_aug + sqrt(lambda+n_aug) * L.col(i);
Xsig_aug.col(i+1+n_aug) = x_aug - sqrt(lambda+n_aug) * L.col(i);
}
/**
* Student part end
*/
// print result
std::cout << "Xsig_aug = " << std::endl << Xsig_aug << std::endl;
// write result
*Xsig_out = Xsig_aug;
}
/**
* expected result:
* Xsig_aug =
* 5.7441 5.85768 5.7441 5.7441 5.7441 5.7441 5.7441 5.7441 5.63052 5.7441 5.7441 5.7441 5.7441 5.7441 5.7441
* 1.38 1.34566 1.52806 1.38 1.38 1.38 1.38 1.38 1.41434 1.23194 1.38 1.38 1.38 1.38 1.38
* 2.2049 2.28414 2.24557 2.29582 2.2049 2.2049 2.2049 2.2049 2.12566 2.16423 2.11398 2.2049 2.2049 2.2049 2.2049
* 0.5015 0.44339 0.631886 0.516923 0.595227 0.5015 0.5015 0.5015 0.55961 0.371114 0.486077 0.407773 0.5015 0.5015 0.5015
* 0.3528 0.299973 0.462123 0.376339 0.48417 0.418721 0.3528 0.3528 0.405627 0.243477 0.329261 0.22143 0.286879 0.3528 0.3528
* 0 0 0 0 0 0 0.34641 0 0 0 0 0 0 -0.34641 0
* 0 0 0 0 0 0 0 0.34641 0 0 0 0 0 0 -0.34641
*/
main.cpp
#include "Dense"
#include "ukf.h"
using Eigen::MatrixXd;
int main() {
// Create a UKF instance
UKF ukf;
/**
* Programming assignment calls
*/
MatrixXd Xsig_aug = MatrixXd(7, 15);
ukf.AugmentedSigmaPoints(&Xsig_aug);
return 0;
}
2.预测sigma点
预测sigma点方法
预测sigma点 c++代码实现
ukf.h
#ifndef UKF_H
#define UKF_H
#include "Dense"
class UKF {
public:
/**
* Constructor
*/
UKF();
/**
* Destructor
*/
virtual ~UKF();
/**
* Init Initializes Unscented Kalman filter
*/
void Init();
/**
* Student assignment functions
*/
void GenerateSigmaPoints(Eigen::MatrixXd* Xsig_out);
void AugmentedSigmaPoints(Eigen::MatrixXd* Xsig_out);
void SigmaPointPrediction(Eigen::MatrixXd* Xsig_out);
void PredictMeanAndCovariance(Eigen::VectorXd* x_pred,
Eigen::MatrixXd* P_pred);
void PredictRadarMeasurement(Eigen::VectorXd* z_out,
Eigen::MatrixXd* S_out);
void UpdateState(Eigen::VectorXd* x_out,
Eigen::MatrixXd* P_out);
};
#endif // UKF_H
ukf.cpp
#include
#include "ukf.h"
using Eigen::MatrixXd;
using Eigen::VectorXd;
UKF::UKF() {
Init();
}
UKF::~UKF() {
}
void UKF::Init() {
}
/**
* Programming assignment functions:
*/
void UKF::SigmaPointPrediction(MatrixXd* Xsig_out) {
// set state dimension
int n_x = 5;
// set augmented dimension
int n_aug = 7;
// create example sigma point matrix
MatrixXd Xsig_aug = MatrixXd(n_aug, 2 * n_aug + 1);
Xsig_aug <<
5.7441, 5.85768, 5.7441, 5.7441, 5.7441, 5.7441, 5.7441, 5.7441, 5.63052, 5.7441, 5.7441, 5.7441, 5.7441, 5.7441, 5.7441,
1.38, 1.34566, 1.52806, 1.38, 1.38, 1.38, 1.38, 1.38, 1.41434, 1.23194, 1.38, 1.38, 1.38, 1.38, 1.38,
2.2049, 2.28414, 2.24557, 2.29582, 2.2049, 2.2049, 2.2049, 2.2049, 2.12566, 2.16423, 2.11398, 2.2049, 2.2049, 2.2049, 2.2049,
0.5015, 0.44339, 0.631886, 0.516923, 0.595227, 0.5015, 0.5015, 0.5015, 0.55961, 0.371114, 0.486077, 0.407773, 0.5015, 0.5015, 0.5015,
0.3528, 0.299973, 0.462123, 0.376339, 0.48417, 0.418721, 0.3528, 0.3528, 0.405627, 0.243477, 0.329261, 0.22143, 0.286879, 0.3528, 0.3528,
0, 0, 0, 0, 0, 0, 0.34641, 0, 0, 0, 0, 0, 0, -0.34641, 0,
0, 0, 0, 0, 0, 0, 0, 0.34641, 0, 0, 0, 0, 0, 0, -0.34641;
// create matrix with predicted sigma points as columns
MatrixXd Xsig_pred = MatrixXd(n_x, 2 * n_aug + 1);
double delta_t = 0.1; // time diff in sec
/**
* Student part begin
*/
// predict sigma points
// avoid division by zero
// write predicted sigma points into right column
// predict sigma points
for (int i = 0; i< 2*n_aug+1; ++i) {
// extract values for better readability
double p_x = Xsig_aug(0,i);
double p_y = Xsig_aug(1,i);
double v = Xsig_aug(2,i);
double yaw = Xsig_aug(3,i);
double yawd = Xsig_aug(4,i);
double v_a = Xsig_aug(5,i);
double v_b = Xsig_aug(6,i);
// predicted state values
double px_p, py_p;
// avoid division by zero
if (fabs(yawd) > 0.001) {
px_p = p_x + v/yawd * ( sin (yaw + yawd*delta_t) - sin(yaw));
py_p = p_y + v/yawd * ( cos(yaw) - cos(yaw+yawd*delta_t) );
} else {
px_p = p_x + v*delta_t*cos(yaw);
py_p = p_y + v*delta_t*sin(yaw);
}
double v_p = v;
double yaw_p = yaw + yawd*delta_t;
double yawd_p = yawd;
// add noise
px_p = px_p + 0.5*v_a*delta_t*delta_t * cos(yaw);
py_p = py_p + 0.5*v_a*delta_t*delta_t * sin(yaw);
v_p = v_p + v_a*delta_t;
yaw_p = yaw_p + 0.5*v_b*delta_t*delta_t;
yawd_p = yawd_p + v_b*delta_t;
// write predicted sigma point into right column
Xsig_pred(0,i) = px_p;
Xsig_pred(1,i) = py_p;
Xsig_pred(2,i) = v_p;
Xsig_pred(3,i) = yaw_p;
Xsig_pred(4,i) = yawd_p;
}
/**
* Student part end
*/
// print result
std::cout << "Xsig_pred = " << std::endl << Xsig_pred << std::endl;
// write result
*Xsig_out = Xsig_pred;
}
main.cpp
#include "Dense"
#include "ukf.h"
using Eigen::MatrixXd;
int main() {
// Create a UKF instance
UKF ukf;
/**
* Programming assignment calls
*/
MatrixXd Xsig_pred = MatrixXd(15, 5);
ukf.SigmaPointPrediction(&Xsig_pred);
return 0;
}
3.根据预测的sigma点预测状态均值和协方差矩阵
预测均值和协方差c++代码实现
ukf.h
#ifndef UKF_H
#define UKF_H
#include "Dense"
class UKF {
public:
/**
* Constructor
*/
UKF();
/**
* Destructor
*/
virtual ~UKF();
/**
* Init Initializes Unscented Kalman filter
*/
void Init();
/**
* Student assignment functions
*/
void GenerateSigmaPoints(Eigen::MatrixXd* Xsig_out);
void AugmentedSigmaPoints(Eigen::MatrixXd* Xsig_out);
void SigmaPointPrediction(Eigen::MatrixXd* Xsig_out);
void PredictMeanAndCovariance(Eigen::VectorXd* x_pred,
Eigen::MatrixXd* P_pred);
void PredictRadarMeasurement(Eigen::VectorXd* z_out,
Eigen::MatrixXd* S_out);
void UpdateState(Eigen::VectorXd* x_out,
Eigen::MatrixXd* P_out);
};
#endif // UKF_H
ukf.cpp
#include
#include "ukf.h"
using Eigen::MatrixXd;
using Eigen::VectorXd;
UKF::UKF() {
Init();
}
UKF::~UKF() {
}
void UKF::Init() {
}
/**
* Programming assignment functions:
*/
void UKF::PredictMeanAndCovariance(VectorXd* x_out, MatrixXd* P_out) {
// set state dimension
int n_x = 5;
// set augmented dimension
int n_aug = 7;
// define spreading parameter
double lambda = 3 - n_aug;
// create example matrix with predicted sigma points
MatrixXd Xsig_pred = MatrixXd(n_x, 2 * n_aug + 1);
Xsig_pred <<
5.9374, 6.0640, 5.925, 5.9436, 5.9266, 5.9374, 5.9389, 5.9374, 5.8106, 5.9457, 5.9310, 5.9465, 5.9374, 5.9359, 5.93744,
1.48, 1.4436, 1.660, 1.4934, 1.5036, 1.48, 1.4868, 1.48, 1.5271, 1.3104, 1.4787, 1.4674, 1.48, 1.4851, 1.486,
2.204, 2.2841, 2.2455, 2.2958, 2.204, 2.204, 2.2395, 2.204, 2.1256, 2.1642, 2.1139, 2.204, 2.204, 2.1702, 2.2049,
0.5367, 0.47338, 0.67809, 0.55455, 0.64364, 0.54337, 0.5367, 0.53851, 0.60017, 0.39546, 0.51900, 0.42991, 0.530188, 0.5367, 0.535048,
0.352, 0.29997, 0.46212, 0.37633, 0.4841, 0.41872, 0.352, 0.38744, 0.40562, 0.24347, 0.32926, 0.2214, 0.28687, 0.352, 0.318159;
// create vector for weights
VectorXd weights = VectorXd(2*n_aug+1);
// create vector for predicted state
VectorXd x = VectorXd(n_x);
// create covariance matrix for prediction
MatrixXd P = MatrixXd(n_x, n_x);
/**
* Student part begin
*/
// set weights
weights(0) = lambda / (lambda + n_aug);
double weight = 0.5 / (lambda + n_aug);
for(int i = 1; i < 2 * n_aug + 1; ++i)
{
weights(i) = weight;
}
// predict state mean
x.fill(0.0);
for (int i = 0; i < 2 * n_aug + 1; ++i)
{ // iterate over sigma points
x = x + weights(i) * Xsig_pred.col(i);
}
// predict state covariance matrix
P.fill(0.0);
for (int i = 0; i < 2 * n_aug + 1; ++i)
{ // iterate over sigma points
// state difference
VectorXd x_diff = Xsig_pred.col(i) - x;
//angle normalization
while (x_diff(3)> M_PI) x_diff(3)-=2.*M_PI;
while (x_diff(3)<-M_PI) x_diff(3)+=2.*M_PI;
P = P + weights(i) * x_diff * x_diff.transpose() ;
}
/**
* Student part end
*/
// print result
std::cout << "Predicted state" << std::endl;
std::cout << x << std::endl;
std::cout << "Predicted covariance matrix" << std::endl;
std::cout << P << std::endl;
// write result
*x_out = x;
*P_out = P;
}
main.cpp
#include "Dense"
#include "ukf.h"
using Eigen::MatrixXd;
using Eigen::VectorXd;
int main() {
// Create a UKF instance
UKF ukf;
/**
* Programming assignment calls
*/
VectorXd x_pred = VectorXd(5);
MatrixXd P_pred = MatrixXd(5, 5);
ukf.PredictMeanAndCovariance(&x_pred, &P_pred);
return 0;
}
UKF Update
测量预测
将预测状态转换为测量空间,定义转换的模型叫测量模型(Measurement model)。
测量模型是一个非线性模型,测量噪音具有单纯的累加效果,因此这里我们不需要扩充噪音,有更好的处理方法。
1.首先,将预测到的sigma点转换到测量空间
2.利用这些转换后的点计算预测测量值的均值和协方差矩阵S
同样,转换后的预测sigma点存储为矩阵的列(col)。

将预测到的sigma点转换到测量空间:

这里,我们不使用扩充噪声矩阵了,故等式中的w_k+1 设为0。
计算均值和协方差:

这里,用测量噪音矩阵R来替代扩充噪音矩阵。
测量预测c++代码实现
ukf.h
#ifndef UKF_H
#define UKF_H
#include "Dense"
class UKF {
public:
/**
* Constructor
*/
UKF();
/**
* Destructor
*/
virtual ~UKF();
/**
* Init Initializes Unscented Kalman filter
*/
void Init();
/**
* Student assignment functions
*/
void GenerateSigmaPoints(Eigen::MatrixXd* Xsig_out);
void AugmentedSigmaPoints(Eigen::MatrixXd* Xsig_out);
void SigmaPointPrediction(Eigen::MatrixXd* Xsig_out);
void PredictMeanAndCovariance(Eigen::VectorXd* x_pred,
Eigen::MatrixXd* P_pred);
void PredictRadarMeasurement(Eigen::VectorXd* z_out,
Eigen::MatrixXd* S_out);
void UpdateState(Eigen::VectorXd* x_out,
Eigen::MatrixXd* P_out);
};
#endif // UKF_H
ukf.cpp
#include
#include "ukf.h"
using Eigen::MatrixXd;
using Eigen::VectorXd;
UKF::UKF() {
Init();
}
UKF::~UKF() {
}
void UKF::Init() {
}
/**
* Programming assignment functions:
*/
void UKF::PredictRadarMeasurement(VectorXd* z_out, MatrixXd* S_out) {
// set state dimension
int n_x = 5;
// set augmented dimension
int n_aug = 7;
// set measurement dimension, radar can measure r, phi, and r_dot
int n_z = 3;
// define spreading parameter
double lambda = 3 - n_aug;
// set vector for weights
VectorXd weights = VectorXd(2*n_aug+1);
double weight_0 = lambda/(lambda+n_aug);
double weight = 0.5/(lambda+n_aug);
weights(0) = weight_0;
for (int i=1; i<2*n_aug+1; ++i) {
weights(i) = weight;
}
// radar measurement noise standard deviation radius in m
double std_radr = 0.3;
// radar measurement noise standard deviation angle in rad
double std_radphi = 0.0175;
// radar measurement noise standard deviation radius change in m/s
double std_radrd = 0.1;
// create example matrix with predicted sigma points
MatrixXd Xsig_pred = MatrixXd(n_x, 2 * n_aug + 1);
Xsig_pred <<
5.9374, 6.0640, 5.925, 5.9436, 5.9266, 5.9374, 5.9389, 5.9374, 5.8106, 5.9457, 5.9310, 5.9465, 5.9374, 5.9359, 5.93744,
1.48, 1.4436, 1.660, 1.4934, 1.5036, 1.48, 1.4868, 1.48, 1.5271, 1.3104, 1.4787, 1.4674, 1.48, 1.4851, 1.486,
2.204, 2.2841, 2.2455, 2.2958, 2.204, 2.204, 2.2395, 2.204, 2.1256, 2.1642, 2.1139, 2.204, 2.204, 2.1702, 2.2049,
0.5367, 0.47338, 0.67809, 0.55455, 0.64364, 0.54337, 0.5367, 0.53851, 0.60017, 0.39546, 0.51900, 0.42991, 0.530188, 0.5367, 0.535048,
0.352, 0.29997, 0.46212, 0.37633, 0.4841, 0.41872, 0.352, 0.38744, 0.40562, 0.24347, 0.32926, 0.2214, 0.28687, 0.352, 0.318159;
// create matrix for sigma points in measurement space
MatrixXd Zsig = MatrixXd(n_z, 2 * n_aug + 1);
// mean predicted measurement
VectorXd z_pred = VectorXd(n_z);
// measurement covariance matrix S
MatrixXd S = MatrixXd(n_z,n_z);
/**
* Student part begin
*/
// transform sigma points into measurement space
for(int i=0; i < 2 * n_aug + 1; ++i)
{
float p_x = Xsig_pred(0,i);
float p_y = Xsig_pred(1,i);
float v = Xsig_pred(2,i);
float yaw = Xsig_pred(3,i);
float yawd = Xsig_pred(4,i);
float th_2 = sqrt(p_x*p_x + p_y*p_y);
float rho_z = th_2;
float yaw_z = atan2(p_y,p_x);
float rhod_z = (p_x*cos(yaw)*v + p_y*sin(yaw)*v) / th_2;
Zsig(0,i) = rho_z;
Zsig(1,i) = yaw_z;
Zsig(2,i) = rhod_z;
}
// calculate mean predicted measurement
z_pred.fill(0.0);
for(int i=0; i < 2 * n_aug + 1; ++i)
{
z_pred = z_pred + weights(i) *Zsig.col(i);
}
// calculate innovation covariance matrix S
S.fill(0.0);
for (int i=0; i < 2*n_aug+1; ++i)
{
VectorXd z_diff = Zsig.col(i) - z_pred;
// angle normalization
while (z_diff(1)> M_PI) z_diff(1)-=2.*M_PI;
while (z_diff(1)<-M_PI) z_diff(1)+=2.*M_PI;
S = S + weights(i) * z_diff * z_diff.transpose();
}
// add measurement noise covariance matrix
MatrixXd R = MatrixXd(n_z,n_z);
R << std_radr*std_radr, 0, 0,
0, std_radphi*std_radphi, 0,
0, 0,std_radrd*std_radrd;
S = S + R;
/**
* Student part end
*/
// print result
std::cout << "z_pred: " << std::endl << z_pred << std::endl;
std::cout << "S: " << std::endl << S << std::endl;
// write result
*z_out = z_pred;
*S_out = S;
}
main.cpp
#include "Dense"
#include "ukf.h"
using Eigen::MatrixXd;
using Eigen::VectorXd;
int main() {
// Create a UKF instance
UKF ukf;
/**
* Programming assignment calls
*/
VectorXd z_out = VectorXd(3);
MatrixXd S_out = MatrixXd(3, 3);
ukf.PredictRadarMeasurement(&z_out, &S_out);
return 0;
}
预测结果如下:
z_pred:
6.12155
0.245993
2.10313
S:
0.0946171 -0.000139447 0.00407016
-0.000139447 0.000617548 -0.000770652
0.00407016 -0.000770652 0.0180917
Update之更新状态
更新状态c++代码实现
void UKF::UpdateState(VectorXd* x_out, MatrixXd* P_out) {
// set state dimension
int n_x = 5;
// set augmented dimension
int n_aug = 7;
// set measurement dimension, radar can measure r, phi, and r_dot
int n_z = 3;
// define spreading parameter
double lambda = 3 - n_aug;
// set vector for weights
VectorXd weights = VectorXd(2*n_aug+1);
double weight_0 = lambda/(lambda+n_aug);
double weight = 0.5/(lambda+n_aug);
weights(0) = weight_0;
for (int i=1; i<2*n_aug+1; ++i) {
weights(i) = weight;
}
// create example matrix with predicted sigma points in state space
MatrixXd Xsig_pred = MatrixXd(n_x, 2 * n_aug + 1);
Xsig_pred <<
5.9374, 6.0640, 5.925, 5.9436, 5.9266, 5.9374, 5.9389, 5.9374, 5.8106, 5.9457, 5.9310, 5.9465, 5.9374, 5.9359, 5.93744,
1.48, 1.4436, 1.660, 1.4934, 1.5036, 1.48, 1.4868, 1.48, 1.5271, 1.3104, 1.4787, 1.4674, 1.48, 1.4851, 1.486,
2.204, 2.2841, 2.2455, 2.2958, 2.204, 2.204, 2.2395, 2.204, 2.1256, 2.1642, 2.1139, 2.204, 2.204, 2.1702, 2.2049,
0.5367, 0.47338, 0.67809, 0.55455, 0.64364, 0.54337, 0.5367, 0.53851, 0.60017, 0.39546, 0.51900, 0.42991, 0.530188, 0.5367, 0.535048,
0.352, 0.29997, 0.46212, 0.37633, 0.4841, 0.41872, 0.352, 0.38744, 0.40562, 0.24347, 0.32926, 0.2214, 0.28687, 0.352, 0.318159;
// create example vector for predicted state mean
VectorXd x = VectorXd(n_x);
x <<
5.93637,
1.49035,
2.20528,
0.536853,
0.353577;
// create example matrix for predicted state covariance
MatrixXd P = MatrixXd(n_x,n_x);
P <<
0.0054342, -0.002405, 0.0034157, -0.0034819, -0.00299378,
-0.002405, 0.01084, 0.001492, 0.0098018, 0.00791091,
0.0034157, 0.001492, 0.0058012, 0.00077863, 0.000792973,
-0.0034819, 0.0098018, 0.00077863, 0.011923, 0.0112491,
-0.0029937, 0.0079109, 0.00079297, 0.011249, 0.0126972;
// create example matrix with sigma points in measurement space
MatrixXd Zsig = MatrixXd(n_z, 2 * n_aug + 1);
Zsig <<
6.1190, 6.2334, 6.1531, 6.1283, 6.1143, 6.1190, 6.1221, 6.1190, 6.0079, 6.0883, 6.1125, 6.1248, 6.1190, 6.1188, 6.12057,
0.24428, 0.2337, 0.27316, 0.24616, 0.24846, 0.24428, 0.24530, 0.24428, 0.25700, 0.21692, 0.24433, 0.24193, 0.24428, 0.24515, 0.245239,
2.1104, 2.2188, 2.0639, 2.187, 2.0341, 2.1061, 2.1450, 2.1092, 2.0016, 2.129, 2.0346, 2.1651, 2.1145, 2.0786, 2.11295;
// create example vector for mean predicted measurement
VectorXd z_pred = VectorXd(n_z);
z_pred <<
6.12155,
0.245993,
2.10313;
// create example matrix for predicted measurement covariance
MatrixXd S = MatrixXd(n_z,n_z);
S <<
0.0946171, -0.000139448, 0.00407016,
-0.000139448, 0.000617548, -0.000770652,
0.00407016, -0.000770652, 0.0180917;
// create example vector for incoming radar measurement
VectorXd z = VectorXd(n_z);
z <<
5.9214, // rho in m
0.2187, // phi in rad
2.0062; // rho_dot in m/s
// create matrix for cross correlation Tc
MatrixXd Tc = MatrixXd(n_x, n_z);
/**
* Student part begin
*/
// calculate cross correlation matrix
for(int i=0; i < 2 * n_aug + 1; i++)
{
VectorXd x_diff = Xsig_pred.col(i) - x;
// angle normalization
while (x_diff(3)> M_PI) x_diff(3)-=2.*M_PI;
while (x_diff(3)<-M_PI) x_diff(3)+=2.*M_PI;
VectorXd z_diff = Zsig.col(i) - z_pred;
// angle normalization
while (z_diff(1)> M_PI) z_diff(1)-=2.*M_PI;
while (z_diff(1)<-M_PI) z_diff(1)+=2.*M_PI;
Tc = Tc + weights(i)*x_diff *z_diff.transpose();
}
// calculate Kalman gain K;
MatrixXd K = Tc * S.inverse();
// update state mean and covariance matrix
VectorXd z_diff = z - z_pred;
// angle normalization
while (z_diff(1)> M_PI) z_diff(1)-=2.*M_PI;
while (z_diff(1)<-M_PI) z_diff(1)+=2.*M_PI;
// update state mean and covariance matrix
x = x + K * z_diff;
P = P - K*S*K.transpose();
/**
* Student part end
*/
// print result
std::cout << "Updated state x: " << std::endl << x << std::endl;
std::cout << "Updated state covariance P: " << std::endl << P << std::endl;
// write result
*x_out = x;
*P_out = P;
}
预测结果如下:
Updated state x:
5.92276
1.41823
2.15593
0.489274
0.321338
Updated state covariance P:
0.00361579 -0.000357881 0.00208316 -0.000937196 -0.00071727
-0.000357881 0.00539867 0.00156846 0.00455342 0.00358885
0.00208316 0.00156846 0.00410651 0.00160333 0.00171811
-0.000937196 0.00455342 0.00160333 0.00652634 0.00669436
-0.00071719 0.00358884 0.00171811 0.00669426 0.00881797
噪音参数和评估选择
对于CTRV模型,有两个参数定义了过程噪声:

分别代表了纵向加速度噪声(您可能会看到这称为线性加速度) 和 偏航加速度噪声(也称为角加速度)
在项目中,这两个值都需要调整。为了得到有效的解决方案,您必须测试不同的值。在视频中,dominik提到使用
![]()
作为跟踪车辆的起点。在UKF项目中,您将跟踪自行车而不是车辆。所以9可能不是一个合适的加速度噪声参数。调谐将涉及:
猜测适当的参数值
运行UKF过滤器
决定结果是否足够好
调整参数并重复该过程
如何选择噪音参数和评估选择,这不仅适用于无损卡尔曼滤波,同样适用于贝叶斯滤波器。
如何选择噪音参数
直线加速度噪声参数直观
偏航加速度噪声参数直观
测量噪声参数
测量噪声参数表示传感器测量的不确定性。一般来说,制造商将在传感器手册中提供这些值。在UKF项目中,不需要调整这些参数。

怎么评估选择
滤波器的一致性检查
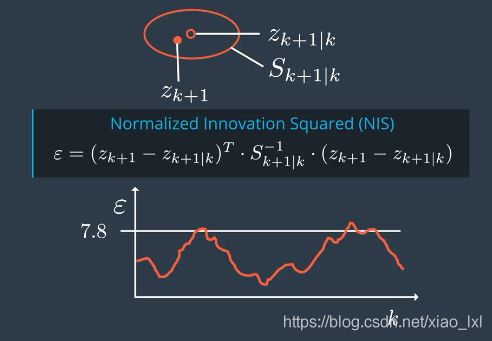
NIS,Normalized Innovation Squared ,归一化新息平方
新息是预测测量值和实际测量值之间的差,
归一化是指相对于矩阵S的协方差而言,因此我们这里有矩阵S的逆。
NIS只是一个标量数字,计算非常简单,如下图公式。NIS的值分布符合卡方分布,

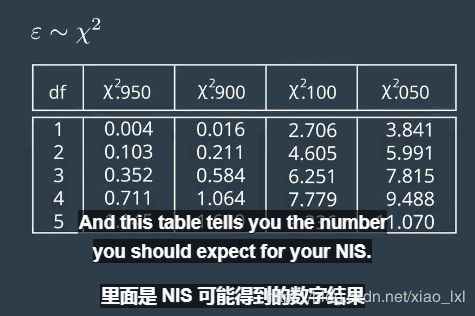
df指自由度,这里指测量空间的维度。
举个例子,假设 第三行

第一列0.95代表在统计意义上,所有情况下有95%的概率,你的NIS会超过0.352;
最后一列0.5代表在统计意义上,所有情况下有5%的概率,你的NIS会超过0.7815;
假设本例中,所有情况下有5%的概率,你的NIS会超过0.7815,若是如下图所示,则表明正常,
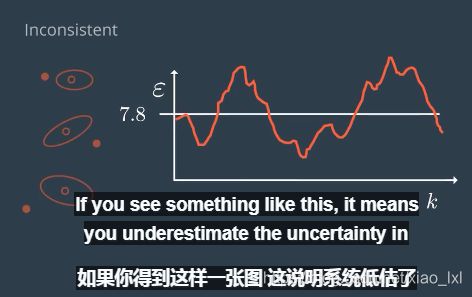
如果得到这样一张图,则说明系统低估了不确定性。
如果得到下面这样一张图,则说明系统高估了不确定性。你估算的精确度比你
想的要高。
不幸的是,NIS测试不会告诉你错误原因。但至少它提供了一些反馈信息。
例如,在本例中,你可以尝试降低过程噪音,然后再试。