汉诺塔问题

刚开始学c语言的时候就从递归上认识了汉诺塔问题，但是当时并没有看懂它的精髓所在，现在数据结构要求用栈和非递归的方式来解答这个问题，于是好好研究了下这个问题，现在想做个总结。

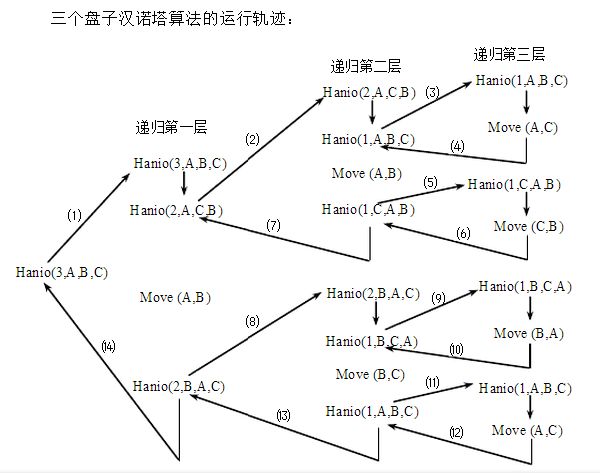
汉诺塔问题：古代有一个梵塔，塔内有三个座A、B、C，A座上有64个盘子，盘子大小不等，大的在下，小的在上。有一个和尚想把这64个盘子从A座移到C座，但每次只能允许移动一个盘子，并且在移动过程中，3个座上的盘子始终保持大盘在下，小盘在上。在移动过程中可以利用B柱，要求打印移动的步骤。

分析：如果A上只有一个盘子，只需直接将盘子从A->C;否则，若A上有n个盘子，则先利用C柱，将A上的n-1个盘子移到B上，再将第n个盘子移到C上。然后，同样的，利用C柱，将B柱上的n-2个盘子移到A柱上，再将第n-1个盘子移到C上，就这样利用递归，直到最后一个盘子移到C柱上。设移动次数为H(n).
H⑴ = 1 
H(n) = 2*H(n-1）+1 (n>1）
那么我们很快就能得到H(n）的一般式：
H(n) = 2^n - 1 (n>0)

简单的C语言代码如下：

1 #include 
2 void hanoi(int n, char A, char B, char C) 
3 {
4     if(n == 1) 
5        printf("Move sheet %d from %c to %c\n", n, A, C);
6    else 
7    {
8        hanoi(n-1, A, C, B);
9        printf("Move sheet %d from %c to %c\n", n, A, C);
10        hanoi(n-1, B, A, C);
11    }
12 }
13 int main() 
14 {
15    int n;
16    printf("Input the number of dishes:\n");
17    scanf("%d", &n);
18    hanoi(n, 'A', 'B', 'C');
19    return 0;
20 }

短短几行代码，利用递归就能将这么复杂的问题解决。 刚开始的时候看不懂，当n >1时，每执行到第8行就跳出hanio函数再进入hanio函数,那后面的事怎么执行的？在这里我想说一下递归的实质。

递归函数调用的本质，系统会将本次函数调用的场景（参数，局部变量，返回地址等）保存在一个栈队列中，系统会不停地往该栈队列压入函数调用的场景，直到达到递归函数的出口为止，到达出口后，再依次将函数场景弹出栈队列，恢复相应的函数场景，完成该次函数调用。

注意：在某个函数调用时，系统会将下一行代码的地址保存在这个场景里，即记录下了返回地址，即在结束这个函数后，系统返回到保存好的返回地址处继续执行。
这也就解释了这个递归是怎样打印出每次移动的操作的。
其次还有个问题，就是函数形参实参的问题，有些同学可能没有看懂，以n = 3为例：(模拟递归时栈的操作，下面为栈底）

n的值 地址 发盘站 中转站 接盘站 移动序号
n = 1 5 A B C （1）
n = 2 9 A C B （2）
n = 3 9 A B C

n的值 地址 发盘站(A) 中转站(B) 接盘站(C) 移动序号
n = 1 5 C A B （3）
n = 2 10 C A B
n = 3 9 A B C ( 4 )

n的值 地址 发盘站(A) 中转站(B) 接盘站(C) 移动序号
n = 1 5 B C A （5）
n = 2 9 B A C （6）
n = 2 10 B A C

n的值 地址 发盘站(A) 中转站(B) 接盘站(C) 移动序号
n = 1 5 A B C （7）

（Move()函数就是用来描述移动轨迹的）

可知形参是用来标定谁是发盘的，中转的，还是接盘的，而实参则是下面所存储的。
于是到这里就应该搞懂了汉诺塔问题的实质啦，接下来看不同的代码实现。

#include
#include 
#define MaxSize 30 
typedef struct 
    {   
        int data[MaxSize];  
        char name;
        int top; 
    }*SqStack;  
void InitStack(SqStack  &s)  /*初始化栈*/ 
{   
    s.data=(int*)malloc(MaxSize*sizeof(int));  
    s->top=-1;
}
int Push(SqStack &s,int e)   /*进栈*/ 
{   
    if(s->top==MaxSize-1)   
        return 0;
    s->top++;
    s->data[s->top]=e;  
    return 1;
}   
int Pop(SqStack &s,int &e)  /*出栈*/ 
{   
    if(s->top==-1)   
        return 0;  
    e=s->data[s->top]; 
    s->top--; 
    return 1;
}    
int Hanoi(int n,SqStack &a,SqStack &b,SqStack &c)
{   
    static int i=0;  
    if(n==1)  
    {    
        Move(a,c);  
        i++; 
    }  
    else  
    {    
        Hanoi(n-1,a,c,b);   
        Move(a,c);   i++;    
        Hanoi(n-1,b,a,c);  
    }   
    return i; 
}   
void Move(SqStack &a,SqStack &b) 
{
   int i;  
   Pop(a,i);  
   printf("Move %d from %c to %c.\n", i, a->name, b->name);
   Push(b,i); 
 }

void main() 
{   int n,i;   
    SqStack a,b,c;  
    InitStack(a);  InitStack(b);  InitStack(c);  
    a->name='A';  b->name='B';  c->name='C'; 
    printf("请输入汉诺塔中圆环的个数n: ");  
    scanf("%d",&n); 
    for(int t=n;t>0;t--)   Push(a,t);  
    i=Hanoi(n,a,b,c);  
    printf("总共需要移动的次数为：%d次\n",i);
}  

只要弄懂了原理，程序写出来很快，再来看看非递归的程序怎么实现：

定义从小到大的盘子序号分别为1，2，……n。
可以用一个1到2^n - 1的2进制序列可以模拟出n个盘子的汉诺塔过程中被移动的盘子的序号序列。
即给定一个n，我们通过0到2^n - 1序列可以判断出任意一步应该移动那个盘子。
判断方法：第m步移动的盘子序号是m用二进制表示的最低位bit为1的位置。
证明： n = 1，显然成立。
假设n = k 成立。
n = k + 1时，对应序列1到2^(k+1) - 1，显然这个序列关于2^k左右对称。
假设我们要把k + 1个盘子从A移动C。
那么2^k可以对应着Move(k + 1, A, C)。 1 到 2^k - 1 根据假设可以
对应Hanoi(A, B, C, k)。至于2^k + 1 到 2^(k + 1) - 1把最高位的1去掉对应序列变成1到2^k - 1，显然2^k + 1 到 2^(k + 1) - 1和1到2^k - 1这两个序列中的对应元素的最低位bit为1的位置相同。因此2^k + 1 到 2^(k + 1) - 1可以对应Hanoi(B, C，A，k)。
所以对n = k + 1也成立。

下面讨论第m步应该移动对应的盘子从哪到哪？
定义顺序为 A->B->C->A, 逆序为C->B->A->C。
性质对n个盘子的汉诺塔,任意一个盘子k(k <= n)k在整个汉诺塔的移动过程中要么一直顺序的，要么一直逆序的。而且如果k在n个盘子移动过程的顺序和k - 1(如果k > 1)以及k + 1(如果k < n)的顺序是反序。
比如：n = 3
1 A->C
2 A->B
1 C->B
3 A->C
1 B->A
2 B->C
1 A->C
其中1的轨迹A->C->B->A>C逆序，2的轨迹A->B->C顺序，3的轨迹A->C逆序
证明：假设n <= k成立
对于n = k + 1 根据递归算法
Hanoi(A，C，B，k + 1) = Hanoi(A, B, C, k) + Move(A, C, k + 1) + Hanoi(B, C，A，k);
整个过程中盘子k + 1只移动一次A->C为逆序对应着2^k。
对于任意盘子m < k + 1,
m盘子的移动由两部分组成一部分是前半部分Hanoi(A, B, C, k)以及后半部分的Hanoi(B, C，A，k)组成。显然有如果m在Hanoi(A, C, B, k)轨迹顺序的话，则m在Hanoi(A, B, C, k)以及Hanoi(B, C，A，k)都是逆序。反之亦然。这两部分衔接起来就会证明m在Hanoi(A，C，B，k)和Hanoi(A，C，B，k + 1)中是反序的。
同时有Hanoi塔中最大的盘子永远是逆序且只移动1步，A->C。
这样的话：
m = k + 1，在Hanoi(A，C，B，k + 1)中是逆序。
m = k，由于在Hanoi(A，C，B，k)中是逆序的，所以Hanoi(A，C，B，k + 1)中是顺序的。
m = k - 1，由于在Hanoi(A，C，B，k - 1)是逆序的，所以Hanoi(A，C，B，k)是顺序的，所以Hanoi(A，C，B，k + 1)是逆序的。
依次下去……
结论得证。
总结：在n个汉诺中n， n - 2, n - 4……是逆序移动，n - 1， n - 3，n - 5……是顺序移动。

#include 
using namespace std;
int main()
{
 int n;
 cin >> n;
 char order[2][256];
 char pos[64];
 order[0]['A'] = 'B';
 order[0]['B'] = 'C';
 order[0]['C'] = 'A';
 order[1]['A'] = 'C';
 order[1]['B'] = 'A';
 order[1]['C'] = 'B'; //0是顺序 1是逆序
 int index[64]; //确定轨迹的顺序还是逆序
 int i, j, m;
 for(i = n; i > 0; i -= 2)
   index[i] = 1;
 for(i = n - 1; i > 0; i -= 2)
   index[i] = 0;
 memset(pos, 'A', sizeof(pos)); //将pos的每个元素置为A
 for(i = 1; i < (1 << n); i ++)
{
 for(m = 1, j = i; j%2 == 0; j/=2, m ++);  //m用二进制表示的最低位bit为1的位置
 cout << m <<" : "<< pos[m]  <<" --> " << order[index[m]][pos[m]] << endl;
 pos[m] = order[index[m]][pos[m]];
}
 return 0;
}