chenchen2005:NOIP2017-S

设 A和 B 是两个长为 n 的有序数组，现在需要将 A 和 B合并成一个排好序的数组，请问任何以元素比较作为基本运算的归并算法最坏情况下至少要做 ( ) 次比较。

解释：
归并排序的最坏情况，则为每次分的两边的大小都是1,和n-1个。这样的话，分开归并的次数就最多，所以就为logn次，又因为合并时要循环n次，则为$$O(n\ast logn)$$

小明要去南美洲旅游，一共乘坐三趟航班才能到达目的地，其中第 1 个航班准点的概率是 0.9，第 2 个航班准点的概率为 0.8，第 3 个航班准点的概率为 0.9。如果存在第 i 个 (i=1,2) 航班晚点，第 i+1 个航班准点，则小明将赶不上第 i+1个航班，旅行失败；除了这种情况，其他情况下旅行都能成功。请问小明此次旅行成功的概率是___。

解释；
大致思想：成功的概率等于1-失败的概率，
由题可知，失败的情况和概率有如下两种

情况一	情况二
0.1×0.8	0.2×0.9

所以答案就是：
$$1-0.1\times 0.8-0.2\times 0.9=1-0.26=0.741-0.1\times 0.8-0.2\times 0.9=1-0.26=0.74$$

3.如下图所示，A 到 B 是连通的。假设删除一条细的边的代价是 1，删除一条粗的边的代价是 2，要让 A、B 不连通，最小代价是_____（2 分），最小代价的不同方案数是_____（3 分）。（只要有一条删除的边不同，就是不同的方案）

解释：
第一步将它标号：

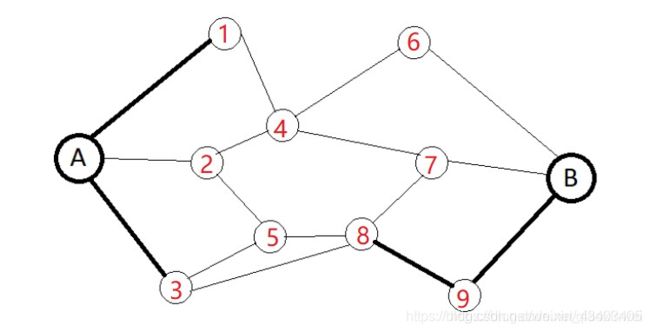
可以从图中看出，要让 A、B 不连通，最小代价是 4。
想求方案数，我们可以把与B相连的连通块从小到大遍历一遍，找到去掉代价为4的边使其断开即可：

• 结点B，删除6B、7B、9B
• 结点6和B连通，删除46、7B、9B
• 结点9和B连通，删除6B、7B、89
• 结点6、9、B连通，删除46、7B、89
• 结点7、8、9、B连通，删除38、47、58、6B
• 结点6、7、8、9、B连通，删除38、46、47、58
• 结点4、6、7、8、9、B连通，删除14、24、38、58
• 结点2、4、6、7、8、9、B连通，删除14、A2、38、58
• 结点2、4、5、6、7、8、9、B连通，删除14、A2、35、38

（最长路径）给定一个有向无环图，每条边长度为 1，求图中的最长路径长度。

输入：第一行是结点数 n（不超过100）和边数 m，接下来 m 行，每行两个整数 a，b，表示从结点 a 到结点 b 有一条有向边。结点标号从 0 到 (n-1) 。

输出：最长路径长度。

提示：先进行拓扑排序，然后按照拓扑序计算。

#include 
using namespace std;
int n, m, i, j, a, b, head, tail, ans;
int graph[100][100];        /* 用邻接矩阵存储图 */
int degree[100];            /* 记录每个结点的入度 */
int len[100];               /* 记录以各结点为终点的最长路径长度 */
int queue[100];             /* 存放拓扑排序结果 */
int main(){
    cin >> n >> m;
    for (i = 0; i < n; i++)
        for (j = 0; j < n; j++)
            graph[i][j] = 0;
    for (i = 0; i < n; i++)
        degree[i] = 0;
    for (i = 0; i < m; i++){
        cin >> a >> b;
        graph[a][b] = 1;
        ___(1)___ ;
    }
    tail = 0;
    for (i = 0; i < n; i++)
        if (___(2)___){
            queue[tail] = i;
            tail++;
        }
    head = 0;
    while (tail < n - 1){
        for (i = 0; i < n; i++)
            if (graph[queue[head]][i] == 1){
                ___(3)___ ;
                if (degree[i] == 0){
                    queue[tail] = i;
                    tail++;
                }
            }
        ___(4)___ ;
    }
    ans = 0;
    for (i = 0; i < n; i++){
        a = queue[i];
        len[a] = 1;
        for (j = 0; j < n; j++)
            if (graph[j][a] == 1 && len[j] + 1 > len[a])
                len[a] = len[j] + 1;
        if (___(5)___)
            ans = len[a];
    }
    cout << ans << endl;
    return(0);
}

①a到b有一条边，所以b的入度+1
②求拓扑序列模板将入度为零的入队
③模板，入队后将入度减一
④出队
⑤打擂台求最大长度
$$完$$