chenchen2005：NOIP2016-J

下面是NOIP2016普及组初赛错题整理

一棵二叉树如右图所示，若采用二叉树链表存储该二叉树（各个结点包括结点的数据、左孩子指针、右孩子指针）。如果没有左孩子或者右孩子，则对应的为空指针。那么该链表中空指针的数目为（ ）

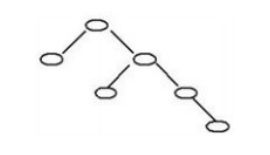
解释：把每一个叶子结点和只有一个孩子的结点算一下就行，所以是6

G 是一个非连通简单无向图，共有 28 条边，则该图至少有（ ）个顶点。
解释：根据公式$$(8-1)\ast 8/2$$得到28条边，然后增加一个节点使其成为非连通图。所以为9

（交朋友）根据社会学研究表明，人们都喜欢找和自己身高相近的人做朋友。 现在有 n名身高两两不相同的同学依次走入教室，调查人员想预测每个人在走入教室的瞬间最想和已经进入教室的哪个人做朋友。当有两名同学和这名同学的身高差一样时，这名同学会更想和高的那个人做朋友。比如一名身高为 1.80米的同学进入教室时，有一名身高为 1.79米的同学和一名身高为 1.81 米的同学在教室里，那么这名身高为 1.80米的同学会更想和身高为 1.81 米的同学做朋友。对于第一个走入教室的同学我们不做预测。

由于我们知道所有人的身高和走进教室的次序，所以我们可以采用离线的做法来解决这样的问题，我们用排序加链表的方式帮助每一个人找到在他之前进入教室的并且和他身高最相近的人。

#include 
using namespace std;
#define MAXN 200000
#define infinity 2147483647

int answer[MAXN], height[MAXN], previous[MAXN], next[MAXN]; int rank[MAXN];
int n;

void sort(int l, int r) {
    int x = height[rank[(l + r) / 2]], i = l, j = r, temp;
    while (i <= j)
    {
        while (height[rank[i]] < x) i++;
        while (height[rank[j]] > x) j--;
        if ( ___(1)___ ) {
            temp = rank[i]; rank[i] = rank[j]; rank[j] = temp;
             i++; j--;
        }
    }
    if (i < r) sort(i, r);
    if (l < j) sort(l, j);
}

int main()
{
    cin >> n;
    int i, higher, shorter;
    for (i = 1; i <= n; i++) {
        cin >> height[i];
        rank[i] = i;
    }
    sort(1, n);
    for (i = 1; i <= n; i++) {
        previous[rank[i]] = rank[i - 1];
           ___(2)___ ;
    }
    for (i = n; i >= 2; i--){
        higher = shorter = infinity;
        if (previous[i] !=0)
            shorter = height[i] - height[previous[i]];
        if (next[i] != 0)
            ___(3)___ ;
        if ( ___(4)___ )
            answer[i] = previous[i];
        else
            answer[i] = next[i];
        next[previous[i]] = next[i];
        ___(5)___ ;
    }
    for (i = 2; i <= n; i++)
        cout << i << ":" << answer[i];
    return 0;
}

height表示高度，answer表示最终答案，previous表示前面的元素，next表示后面元素，rank表示高度排名
①快排模板
②模仿上面的previous的写法就行
③也是模仿上方的shorter写，只不过要改变顺序
④可以看出shorter就是与矮的人的身高差，higher就是与高的人的身高差，然后根据题目就可以看出来了
⑤还是模仿上面的next写