进化计算-遗传算法之史上最全选择策略
![]()
获取更多资讯,赶快关注上面的公众号吧!
文章目录
- 第十九章 遗传算法-史上最全选择策略
- 19.1 轮盘赌选择(Roulette-wheel selection)
- 19.2 锦标赛选择(Tournament selection)
- 19.3 截断选择(Truncation selection)
- 19.4 蒙特卡洛选择(Monte Carlo selection)
- 19.5 概率选择(Probability selection)
- 19.6 线性排序选择(Linear-rank selection)
- 19.7 指数排序选择(Exponential-rank selection)
- 19.8 玻尔兹曼选择(Boltzmann selection)
- 19.9 随机遍历选择(Stochastic-universal selection)
- 19.10 精英选择(Elite selection)
第十九章 遗传算法-史上最全选择策略
从群体中选择优胜的个体,淘汰劣质个体的操作叫选择。选择算子有时又称为再生算子(reproduction operator)。选择的目的是把优化的个体(或解)直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的,目前常用的选择算子有以下几种:轮盘赌、锦标赛、截断选择、蒙特卡洛选择、概率选择、线性排序、指数排序、玻尔兹曼、随机遍历、精英选择等,接下来作详细介绍。
19.1 轮盘赌选择(Roulette-wheel selection)
轮盘赌选择法是依据个体的适应度值计算每个个体在子代中出现的概率,并按照此概率随机选择个体构成子代种群,因此该方法也被称为适应度比例法。轮盘赌选择策略的出发点是适应度值越好的个体被选择的概率越大。因此,在求解最大化问题的时候,我们可以直接采用适应度值来进行选择。但是在求解最小化问题的时候,我们必须首先将问题的适应度函数进行转换(如采用倒数或相反数),以将问题转化为最大化问题。
为了计算选择概率P(i),需要用到每个个体i的适应度值fi:
P ( i ) = f i ∑ j = 0 N − 1 f j (1) P\left( i \right) = \frac{{{f_i}}}{{\sum\nolimits_{j = 0}^{N - 1} {{f_j}} }}\tag 1 P(i)=∑j=0N−1fjfi(1)
从给定种群中选出M个个体就等价于旋转M次轮盘,在选择个体前实际上不必对种群中的个体进行排序。注意式(1)中默认假定所有适应度值为正值,且适应度值之和不为0。为了能够处理负的适应度值,可以采用一种改进的公式来计算选择概率。
P ′ ( i ) = f i − f min ∑ j = 0 N − 1 ( f j − f min ) (2) P^{\prime}(i)=\frac{f_{i}-f_{\min }}{\sum_{j=0}^{N-1}\left(f_{j}-f_{\min }\right)}\tag 2 P′(i)=∑j=0N−1(fj−fmin)fi−fmin(2)
其中 f min = min i ∈ [ 0 , N ) { f i , 0 } f_{\min }=\min _{i \in[0, N)}\left\{f_{i}, 0\right\} fmin=mini∈[0,N){fi,0}。
设最差的适应度值为fmin,如果其为负值,那么选择概率为0(因为分子为0)。而对于校正后的适应度之和(即分母)为0的情况,可以将所有个体的选择概率设为 1 N \frac{1}{N} N1。
19.2 锦标赛选择(Tournament selection)
在锦标赛选择中,从种群中随机采样s个个体(注意:采样是有放回的),然后选择最优的个体进入下一代,只有个体的适应度值优于其他s-1个竞争者时才能赢得锦标赛。注意最差的个体永远不会幸存,而最优的个体在其参与的所有锦标赛中都能获胜。
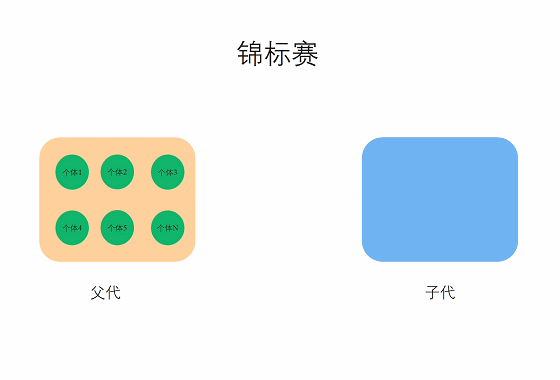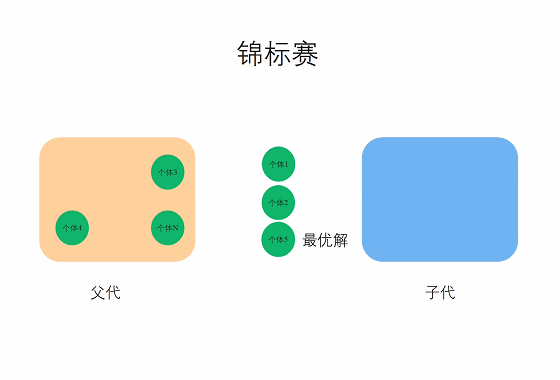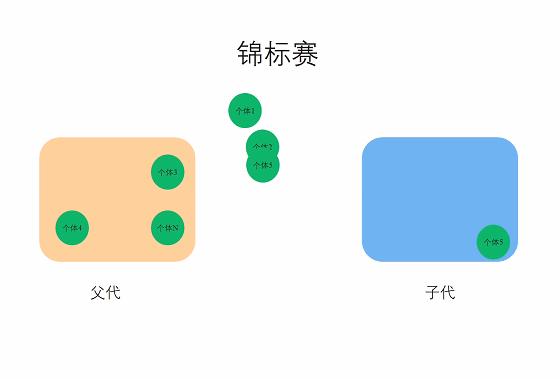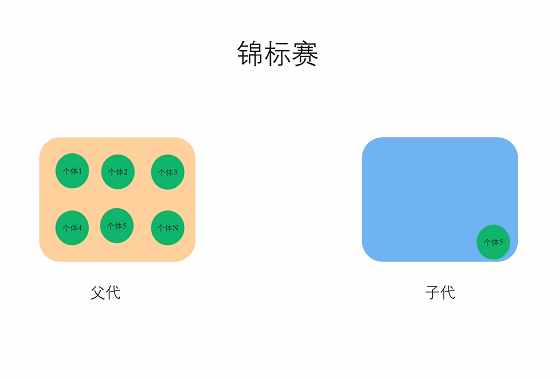
选择压力可以通过改变锦标赛的大小s来改变,对于较大的s值,弱者被选中的机会较小,常见的有二元锦标赛和三元锦标赛等。与适应度值比例选择相比,锦标赛选择由于缺乏随机噪声,在实际应用中经常被使用,同时锦标赛选择也和遗传算法适应度函数的尺度无关,因为只需要比较绝对值大小,不用考虑正负的问题。
19.3 截断选择(Truncation selection)
在截断选择中,根据适应度值对种群中的个体按照从优到劣的顺序进行排序,只有前n个最好的个体被选择进入下一代。截断选择是一种非常基础的选择算法,尽管它的优势在于能够快速地在大量种群中选择个体,但是在实际中并不常用。截断选择是在动植物育种方面的标准方法,按照表现型价值排序,只有最好的动物才会被选择繁殖。
19.4 蒙特卡洛选择(Monte Carlo selection)
蒙特卡洛选择方法从给定的种群中随机选择个体,因此蒙特卡洛选择执行的是随机搜索而不是定向搜索。一般情况下,蒙特卡洛选择用于度量其他选择器的性能。通常选择器的性能要优于蒙特卡洛选择的性能。
19.5 概率选择(Probability selection)
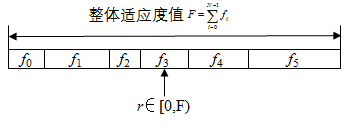
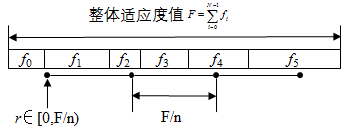
概率选择是适应度比例选择的一种变体,基于选择概率P(i)从给定的种群中选择个体。适应度比例选择工作原理如图1所示。均匀分布的随机数r∈[0,F)通过下面的参数最小化指定了选择哪个个体:
i ← argmin n ∈ [ 0 , N ) { r < ∑ i = 0 n f i } (3) i \leftarrow \underset{n \in[0, N)}{\operatorname{argmin}}\left\{r<\sum_{i=0}^{n} f_{i}\right\}\tag 3 i←n∈[0,N)argmin{r<i=0∑nfi}(3)
概率选择也遵循同样的工作原理,只不过使用个体的选择概率P(i)代表适应度值fi。概率选择不需要对种群进行排序,个体i的选择概率服从二项分布:
P ( i , k ) = ( n k ) P ( i ) k ( 1 − P ( i ) ) n − k P(i, k)=\left(\begin{array}{c}{n} \\ {k}\end{array}\right) P(i)^{k}(1-P(i))^{n-k} P(i,k)=(nk)P(i)k(1−P(i))n−k
其中n为种群大小,k为需要从种群中选出的个体的数量。实现的概率选择器的运行复杂度为O(n+log(n)),而不是O(n2),由于朴素法:对求和概率数组执行二进制(索引)搜索。
19.6 线性排序选择(Linear-rank selection)
当适应度值差别很大时,轮盘赌选择将会出现问题。如果最优染色体的适应度值占适应度值总和的90%,即其占据了轮盘上90%的周长,那么其他染色体被选择到的概率就很低。在线性排序选择中,首先按照适应度值对个体进行排序,最差个体排在第1位,最优个体排在第N位,根据排位先后,线性地分派给染色体i的选择概率P(i):
P ( i ) = 1 N ( n − + ( n + − n − ) i − 1 N − 1 ) (4) P(i)=\frac{1}{N}\left(n^{-}+\left(n^{+}-n^{-}\right) \frac{i-1}{N-1}\right)\tag {4} P(i)=N1(n−+(n+−n−)N−1i−1)(4)
这里 n − N \frac{{{n^ - }}}{N} Nn−是最劣染色体的选择概率, n + N \frac{{{n^ + }}}{N} Nn+是最优染色体的选择概率。值得注意的是,所有的个体得到不同的排名,分别得到不同的选择概率,即使它们拥有相同的适应度值。
19.7 指数排序选择(Exponential-rank selection)
弱线性选择的另一种方案是使用指数函数为排序后的个体分配生存概率:
P ( i ) = ( c − 1 ) c i − 1 c N − 1 (5) P(i)=(c-1) \frac{c^{i-1}}{c^{N}-1}\tag 5 P(i)=(c−1)cN−1ci−1(5)
其中c必须位于区间[0,1)内,c越小最优个体被选择的概率就越大,如果c=0,则设置最优个体被选择的概率为1,而其他所有个体的选择概率为0。c越接近于1,个体间的选择概率越接近。注意,在计算选择概率前,需要对种群按照适应度值进行降序排序。
19.8 玻尔兹曼选择(Boltzmann selection)
玻尔兹曼选择器的选择概率定义如下:
P ( i ) = e b ⋅ f i Z (6) P(i)=\frac{\mathrm{e}^{b \cdot f_{i}}}{Z}\tag 6 P(i)=Zeb⋅fi(6)
其中b是控制选择强度的参数,Z的定义如下:
Z = ∑ i = 1 n e f i (7) Z=\sum_{i=1}^{n} \mathrm{e}^{f_{i}}\tag 7 Z=i=1∑nefi(7)
b>0时,增大了具有高适应度值的个体被选择的概率;b<0时,则降低概率;b=0时,所有个体的选择概率均为 1 N \frac{1}{N} N1 。
19.9 随机遍历选择(Stochastic-universal selection)
随机遍历选择(SUS)是一种根据给定概率以最小化波动概率的方式选择个体的方法。可以将其认为是一种轮盘赌游戏,在轮盘上有p个等间距的点进行旋转。SUS使用一个随机值在等间隔的空间间隔内选择来选择个体。相比较于适应度比例选择法,该方法中较劣个体也有很好的机会被选择,从而奖励了不公平性。该选择方法是由James Baker提出的,展示了其原理,其中n为要选择的个体数量。随机遍历采样保证了选出的子代,比轮盘赌法更加接近希望得到的结果。
19.10 精英选择(Elite selection)
精英选择将一小部分最优的候选解,原封不动的复制到下一代中,这会对性能产生巨大的影响,因为这保证了GA不会浪费时间重新发现以前拒绝的部分解。通过精英主义被保留下来的个体仍然有资格被选为下一代的父代。精英主义也与记忆有关:记住目前找到的最优解。不过精英主义的问题在于会导致GA收敛到局部最优,所以纯粹的精英主义是一场通向最近局部最优的竞争。