概率论03 条件概率
作者:Vamei 出处:http://www.cnblogs.com/vamei 欢迎转载,也请保留这段声明。谢谢!
在概率公理中,我们建立了“概率测度”的概念,并使用“面积”来类比。这是对概率的第一步探索。为了让概率这个工具更加有用,数学家进一步构筑了“条件概率”,来深入探索概率中包含的数学结构。我们可以考虑生活中常见的一个估计:
三个公司开发一块地。A占地20%,B占地30%,C占地50%。三个公司规划的绿地占比不同:A土地中40%规划为绿地,B土地中的30%规划为绿地,C土地中的10%规划为绿地。我想选择绿地最大的一个小区,应该选择哪一个呢?我们可以画图出来:
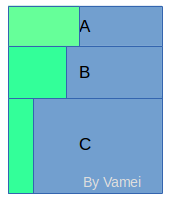
显然,我们需要比较的是A:0.2x0.4,B:0.3x0.1,C:0.5x0.1。这是我们常见的一种情形:整个地区分块,每块有一定的比例。再进一步考虑每一块内部的相对比例。我们要了解的“条件概率”这一概念,就对应这里的“相对比例”。
条件概率:何弃疗
上面公司的不同造成了绿地占比的不同,也就是说,公司这一因素影响了绿地占比。条件概率同样反映了其它因素对事件概率的影响。
比如说,患者康复有一个概率。在接受治疗和放弃治疗的两种条件下,患者康复的概率也不同。下面是患者的统计结果。
| 治疗(T) | 弃疗(NT) | 总数 | |
| 康复(R) | 300 | 100 | 400 |
| 未康复(NR) | 200 | 400 | 600 |
| 总数 | 500 | 500 | 1000 |
所有的1000人中,共有400人康复,总体的康复概率为[$P(R) = 400/1000 = 0.4$]。另一方面,在接受治疗一列,总共有500人。在这500人种,有300人康复。因此,在接受治疗的条件下,康复的概率变成[$ 300/500 = 0.6$]。这个概率值高于总体的康复概率。而放弃治疗的条件下,康复的概率为[$ 100/500 = 0.2$],康复的概率较低 (可恶,为何放弃治疗)。可见,康复率受到是否接受治疗这一条件的影响。
为了表达某一事件(治疗)对另一个事件(康复)概率的影响,概率论中引入条件概率的概念。条件概率记为[$P(R|T) = 300/500 = 0.6$]。R和T是两个事件,即治疗和康复。在治疗(T)的条件下,患者康复(R)的概率为0.6。
(对应文章开始的例子,每个公司的绿地占比为条件概率。比如[$P(绿地|A公司) = 40%$])

不要放弃治疗啊!
条件概率的定义
上面给出了条件概率的粗糙概念。但我们已经了解了概率的公理化体系,因此可以基于公理化体系,更严格的定义条件概率。
定义 如果A和B是两个事件,且[$P(B) \ne 0$]。那么B条件下,A的条件概率为
$$P(A|B) = \frac{P(A \cap B)}{P(B)}$$
这是一个非常直观的概念。回到绿地的例子,这里的意思就是说,我们想要知道A公司的绿地占比[$P(绿地 | A公司)$]的话,可以用A公司占据的绿地面积[$P(A公司 \cap 绿地)$],除以A公司占据土地的面积[$P(A公司)$]。
在上面定义条件概率时,我们使用了概率[$P(A \cap B)$],即A和B同时发生的概率。从频率的角度上来看,是同时符合A和B的样本数除以[$\Omega$]中的样本总数。比如上面治疗和康复的例子,[$P(R \cap T) = 300/1000$]。但[$P(A|B)$]的隐含假设是,B确定要发生,即病人确定康复。符合这样条件的样本只有500个,而不是整个[$\Omega$]的1000个样本。
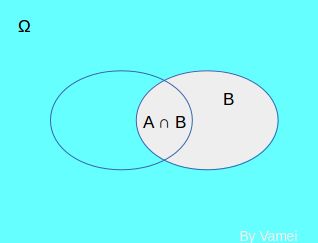
也就是说,当确定B发生时,样本空间不再是[$\Omega$],而是缩小成B。我们在B样本空间中寻找A发生的概率。从上面的图中看,就是[$A \cap B$]的面积(概率测度),除以B占据的面积(概率测度),也就是我们条件概率的定义。
条件概率的相关推论
条件概率有一些很有用的推论:
推论1 A和B为两个事件,且[$P(B) \ne 0$]。那么
$$P(A \cap B) = P(A|B)P(B)$$
这个只是将上面的定义中的等式两侧乘以P(B)。从而允许我们从条件概率,来推导两个事件同时发生的概率。
假设卫星观察到,一个地区某一天有云的概率为[$P(Cloud) = 0.2$]。该地区的地面观测站发现,有云的条件下,当天下雨的为0.5。这是一个条件概率,即[$P(Rain | Cloud) = 0.5$]。那么既下雨又有云的概率为
$$P(Cloud \cap Rain) = P(Cloud) \times P(Rain | Cloud) = 0.2 \times 0.5 = 0.1$$

另一个推论,用于通过已知的条件概率,来计算一个事件的概率
推论2 有事件[$B_1, B_2, ..., B_n$]。如果[$\bigcup_{i=1}^n B_i = \Omega $],两个不同事件互斥([$B_i \cap B_j = \Phi$], 如果[$i \ne j$]),且任意[$P(B_i) \gt 0$]。那么,对于任意事件A
$$P(A) = \sum\limits_{i=1}^n P(A|B_i)P(B_i)$$
这个推论的要点是不同的B事件互斥(不相交),且它们的并集是[$\Omega$]。每个元素都必须且只能进入一个[$B_i$]。在这样的条件下,我们说[$B_1, B_2, ..., B_n$]是样本空间的一个分割(partion)。 这就像二战后的德国被分区占领一样,每个[$B_i$]是一个占领区。
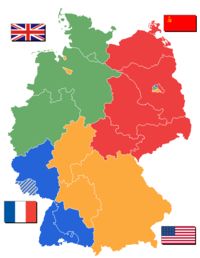
这正是对所有情况“分块”的思想。再根据每个分块中的某个事件的相对比例,乘以分块自身的权重(“块”的概率),我们可以求得该事件的绝对占比。
假设家庭收入分为高(H),中(M),低(L)三类,高收入家庭占20%,中等收入家庭占65%,低收入家庭占15%。如果高收入家庭的拥有汽车的概率为0.8,中等收入家庭的拥有汽车的概率为0.5,低收入家庭的拥有汽车的概率为0.2。那么任意一个家庭的拥车概率为:
$$P(C) = P(C|H)P(H) + P(C|M)P(M) + P(C|L)P(L) = 0.8 \times 0.2 + 0.5 \times 0.65 + 0.2 \times 0.15 = 0.515$$

独立事件
两个事件可以是相互独立的 (independent)。直观的讲,如果事件A发生与否不会影响事件B的概率,那么A与B独立。
我们尝试将这一个概念用条件概率来表达:将B看作A的条件,那么A的条件概率不受B的影响,即:
定义 两个事件A和B,[$P(A) \ne 0$],[$P(B) \ne 0$]。如果[$P(A|B) = P(A)$],或者[$P(B|A) = P(B)$],那么事件A和B是独立事件。
某一条件下的“相对占比”等于任意条件下的“绝对占比”?这是怎么一种情况呢?
我们可以想像这样的情况。水中氢和氧的组成比为2:1 (任意条件下)。而水的三种态(水蒸汽、液态水、冰)中的氢和氧组成也是2:1。也就是说,水的态这一条件对氢氧组成无影响,两者独立。
根据独立事件和条件概率的定义可以推知,如果
$$P(A \cap B) = P(A)P(B)$$
那么A和B独立。
注意,独立事件和互斥事件不同。独立事件是指A发生的概率不影响B。对于互斥事件来说,如果A发生,那么B必然不发生,A的发生影响到了B,所以不是独立事件。比如下雨和不下雨可以看做互斥事件,而下雨和骰子为1可以看做独立事件。
事件[A_1, A_2, ..., A_n]被称为相互独立(mutually independent),如果对于任意子集[A_{i_1},...,A_{i_m}]都有
$$P(A_{i_1} \cap ... \cap A_{i_m}) = P(A_{i_1})...P(A_{i_m})$$
贝叶斯法则
根据上面的定律,我们可以推导出贝叶斯法则(Bayes' Rule)。
贝叶斯法则 如果A和[$B_1, B_2, ..., B_n$]为事件,[$B_i$]互斥,[$\bigcup_{i=1}^n B_i = \Omega$], 且[$P(B_i) \gt 0$]。那么
$$P(B_j|A) = \frac{P(A|B_j)P(B_j)}{\sum\limits_{i=1}^n P(A|B_i)P(B_i)}$$
这个法则是一种求条件概率的方式。
我们使用文章开头的治疗与康复的例子。我们已知治疗和弃疗的条件概率为[$P(R|T) = 0.6$],[$P(R/NT) = 0.2$],而[$P(T) = P(NT) = 0.5$]。
治疗与弃疗互斥(不可能同时治疗又弃疗),且其并集构成全集(要么治疗,要么弃疗,没有其它的可能)。根据贝叶斯法则,
$$P(T|R) = \frac{P(R|T)P(T)}{P(R|T)P(T) + P(R|NT)P(NT)} = \frac{0.6 \times 0.5}{0.6 \times 0.5 + 0.2 \times 0.5} = 0.75$$
即一个康复的人,用药的概率。这与我们在表格中看到的比例相符(400个康复的人中,300个人用药)。
贝叶斯法则常用于求一些比较难以直接获得的条件概率。此外,在机器学习中,也有贝叶斯算法的应用。
练习,编写一个Python函数,用于实现贝叶斯法则的功能。并计算下面的概率:
已知专家预报下雨时,下雨的概率为0.8; 专家预报不下雨时,下雨的概率为0.2。根据以往的经验,专家一年中有30天预报下雨,剩下的天里预报不下雨。问,如果下雨,专家预报的是不下雨的概率为多少?
总结
条件概率
独立事件
贝叶斯法则
欢迎继续阅读“数据科学”系列文章