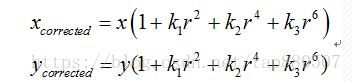内参、外参、畸变参数三种参数与相机的标定方法与相机坐标系的理解

 https://blog.csdn.net/yangdashi888/article/details/51356385

1、 相机参数是三种不同的参数。

 相机的内参数是六个分别为：1/dx、1/dy、r、u0、v0、f。

u0,v0为图像像素坐标系中光轴投影坐标即主点坐标，

1/dx,1/dy分别为在x方向上每个像素的物理尺寸，在y方向上每个像素的物理尺寸，

gama为x,y不垂直时的扭曲系数，一般为0；。

opencv1里的说内参数是4个其为fx、fy、u0、v0。实际其fx=F*Sx，其中的F就是焦距上面的f,Sx是像素/每毫米即上面的dx，其是最后面图里的后两个矩阵进行先相乘，得出的，则把它看成整体，就相当于4个内参。其是把r等于零，实际上也是六个。

dx和dy表示：x方向和y方向的一个像素分别占多少长度单位，即一个像素代表的实际物理值的大小，其是实现图像物理坐标系与像素坐标系转换的关键。u0，v0表示图像的中心像素坐标和图像原点像素坐标之间相差的横向和纵向像素数。

相机的外参数是6个：三个轴的旋转参数分别为（ω、δ、 θ）,然后把每个轴的3*3旋转矩阵进行组合（即先矩阵之间相乘），得到集合三个轴旋转信息的R，其大小还是3*3；T的三个轴的平移参数（Tx、Ty、Tz）。R、T组合成成的3*4的矩阵，其是转换到标定纸坐标的关键。其中绕X轴旋转θ，则其如图：

   注意：在每个视场无论我们能提取多少个角点，我们只能得到四个有用的角点信息，这四个点可以产生8个方程，6个用于求外参，这样每个视场就还赚两个方程来求内参，则其在多一个视场即可求出4个内参。因为六个外参，这就是为什么要消耗三个点用于求外参。

畸变参数是：k1,k2,k3径向畸变系数，p1,p2是切向畸变系数。径向畸变发生在相机坐标系转图像物理坐标系的过程中。而切向畸变是发生在相机制作过程，其是由于感光元平面跟透镜不平行。其如下：

1．径向畸变：产生原因是光线在远离透镜中心的地方比靠近中心的地方更加弯曲径向畸变主要包含桶形畸变和枕形畸变两种。下面两幅图是这两种畸变的示意：

          它们在真实照片中是这样的：

           2.切向畸变：产生的原因透镜不完全平行于图像平面，这种现象发生于成像仪被粘贴在摄像机的时候。下面图片来自于《学习opencv》p413。

其中畸变的形象示意图是如下：

其总的转换关系：

下面是普通摄像头标定后的输出值，其如下：

其中的fx、fy是f/dx、f/dy得出来的值。其中的cx、cy一般不是正好是图像分辨率的一半，其是有偏差的，一般越好的摄像头则其越接近于分辨率的一半。上面例子使用的摄像头是一个普通的1280x720分辨率的摄像头，其偏差还是蛮大的。下面的数据是比较好的摄像头罗技720p的，其分辨率也是1280x720的分辨率。可以看出其更接近分辨率的一半。

2、相机的标定方法与意义：

（一）什么是摄像机标定

    在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立摄像机成像的几何模型,这些几何模型参数就是摄像机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数的过程就称之为摄像机标定。

（一）相机标定的意义

    无论是在图像测量或者机器视觉应用中，摄像机参数的标定都是非常关键的环节，其标定结果的精度及算法的稳定性直接影响摄像机工作产生结果的准确性。因此，做好摄像机标定是做好后续工作的前提，是提高标定精度是科研工作的重点所在。其标定的目的就是为了相机内参、外参、畸变参数。

  其标定方法大概有三种如下：

1.线性标定方法的大概数学公式是：

其求解过程如下：

注意：这种标定是没有考虑到相机畸变的非线性问题，意思是这种标定是

在不考虑相机畸变的情况下使用。

2.非线性标定方法：

当镜头畸变明显时必须引入畸变模型，将线性标定模型转化为非线性标定模型，

通过非线性优化的方法求解相机参数：

3.两步标定法：

   1.Tsai的经典两步法

       概念：Tsai基于 RAC 约束（RadialAlignment Constrain）提出的两步法，在求解过程中将CCD（电耦合器件）阵列感光元的横向间距和纵向间距当作已知参数，求解的摄像机内部参数：有效焦距f；镜头径向畸变系数k1,k2；非确定性尺度因子xs ；图像中心或主点u0,v0。外部参数：世界坐标系与摄像机坐标系之间的旋转矩阵R与平移向量t。

     求解：首先利用最小二乘法求解超定线性方程组，求得模型外部参数；然后求解内部参数，如果摄像机无透镜畸变，可通过一个超定线性方程组解出，如果存在一个以二次多项式近似的径向畸变，则利用一个包含三个变量的目标函数进行优化搜索求解。

  

1.相机坐标系：

相机坐标系是连接图像物理坐标系与世界坐标系的桥梁，其中相机坐标的系的坐标原点是：镜头的光心---其也是相机坐标系里的投影中心。

1.内参数：由于相机坐标系使用的是毫米制的单位，而图像平面使用的像素为单位。内参数的作用就是在这两个坐标系之间进行线性的变化。相机光轴中心Z轴方向与像平面交点称为投影中心，其坐标为，其单位为像素。在图像平面上像素和毫米之间的关系有：

                                                                                                                              （1）

根据小孔成像原理，图像平面上的一点（x,y）对应在相机坐标系下的坐标为：

                                                                                                                                （2）

改写成矩阵形式为：                              

                                                                                                                           （3）

联立1,3式：

                                                                                                          

其中为相机内矩阵参数，一般来说，内阵矩阵数要求解的有（fx,fy,cx,cy）。

 

         

摄像机的透视投影模型（即针孔成像模型）：
       设OXYZ为世界坐标系，uv为以像素为单位的图像坐标系。如果物点P在世界坐标系下的坐标为（X,Y,Z）,对应的图像点p在图像坐标系的坐标为（u，v），可以有：
                 

在该式中，fu、fv、u0、v0只与摄像机内部参数有关，故称矩阵M1为内参数矩阵。
     其中fu ＝ f/dX ,fv = f/dY ,分别称为u轴和v轴上的归一化焦距；f是相机的焦距，dX和dY分别表示传感器u轴和v轴上单位像素的尺寸大小。
    u0和v0则表示的是光学中心，即摄像机光轴与图像平面的交点，通常位于图像中心处，故其值常取分辨率的一半。
现以NiKon D700相机为例进行求解其内参数矩阵：
就算大家身边没有这款相机也无所谓，可以在网上百度一下，很方便的就知道其一些参数——        焦距 f = 35mm   最高分辨率：4256×2832     传感器尺寸：36.0×23.9 mm
根据以上定义可以有：
u0 = 4256/2 = 2128   v0 = 2832/2 = 1416  dx = 36.0/4256   dy = 23.9/2832
fu = f/dx = 4137.8   fv = f/dy = 4147.3
该模型中其他一些参数的含义解释：
  为投影深度，其几何意义是目标点P在摄像机坐标系中坐标的Z分量，一般情况下，该值令为1.
R，t则构成了摄像机的外参数矩阵，分别称为旋转矩阵和平移矩阵。R是一个3X3的矩阵，t则是一个3X1的矩阵。R可以使用四元素法表示也可以使用欧拉角表示，各有各的好处。
摄像机的仿真，可以简单的认为是对内外参数的仿真。只要理解了以上模型中各个量的含义，就可以很容易的模拟一个摄像机。