【tensorflow】4.卷积神经网络详解_MINIST实例
本文中,会搭建一个简单的卷积网络,实现手写体数据集MINIST的识别。
通过本文,可以学到卷积神经网络的一般结构,体会数据的整个流动,重点是体会数据维度的对应关系,理解各层的作用和参数的意义。
2018.5.29更新:重新组织代码。增加测试,采用真实的手写图片进行测试!
采用真实数据做测试,一定要符合MINIST数据集的要求
- label是[0,1,2,3,4,5,6,7,8,9]的顺序标号。
- image数据必须归一化到[0,1]的阈值化图像
一. 卷积神经网络
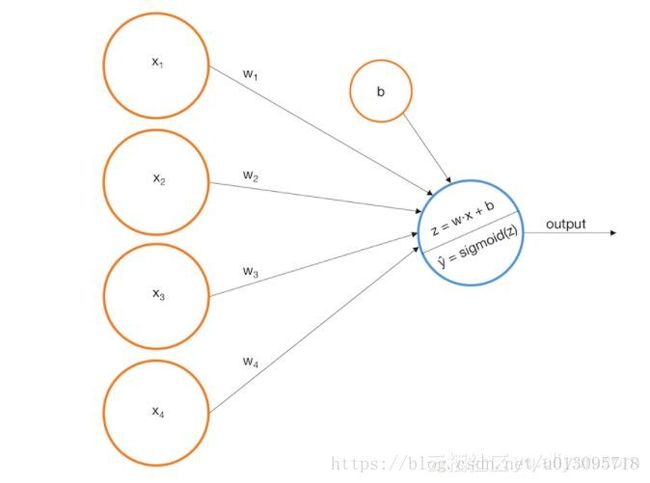
所谓卷积神经网络,即神经元与输入数据经行的运算不是简单的线性运算。一般的神经网络中,隐层的神经元于输入进行的是以下操作:
此处 f(y) f ( y ) 是一个非线性映射,如sigmod函数。如下图
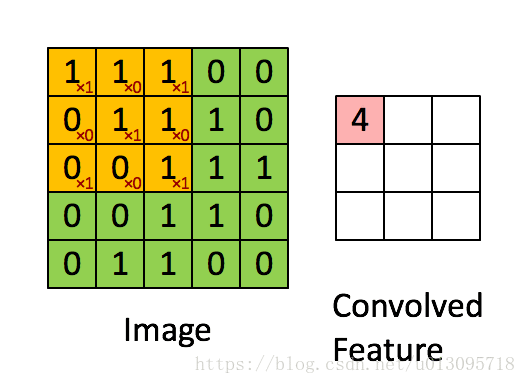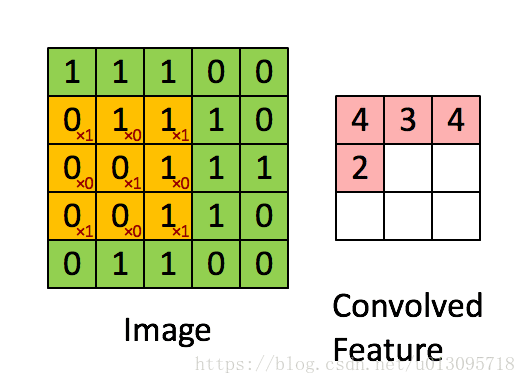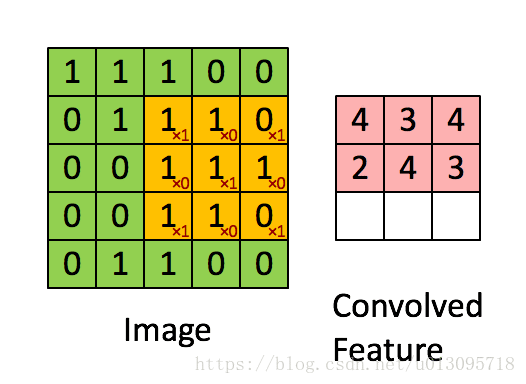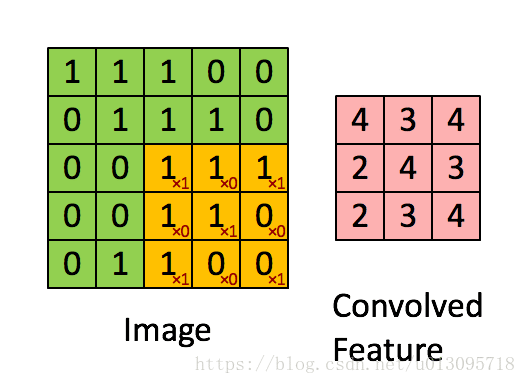
而卷积神经网络的神经元,与输入进行的是卷积操作(表面理解就是按模板权值进行的乘加操作,实际上就是一个有关空间的局部线性叠加)。如下图所示(该图中,边缘没有填充(采用valid策略),所以尺寸缩小了,若填充边缘,则卷积不会改变尺寸)(注意‘尺度’和‘尺寸’的区别)
由于卷积利用了空间特性,故通常在卷积的时候,需要保留原空间信息——即图片最好不要是向量形式,而是原始的矩阵形式。
卷积层,或者说卷积操作有何意义?
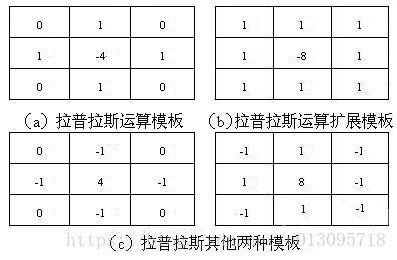
在图像处理中,对图像的滤波通常采用的就是卷积操作,如一个 3×3 3 × 3 的均值滤波器卷积核(kernel)为{{1,1,1},{1,1,1},{1,1,1}},该kernel的作用是均值平滑去噪。而一个laplace kernel可以用来提取图像的边缘信息!其模板如下
所以我们认为卷积层对图像进行一系列的卷积操作,实际上是通过网络学习到的kernel对图像进行信息的提取(比如,若学习到的模板参数正好是laplace模板系数,那么这个neuron进行的就是边缘提取功能)。
网络结构
当然卷积神经网络中,并不是只有卷积层,这里我们来了解以下其他的网络层结构,及其作用。
把握CNN结构,最重要的是掌握样本数据在网络中的流动,维度的变化,尺寸的变化。
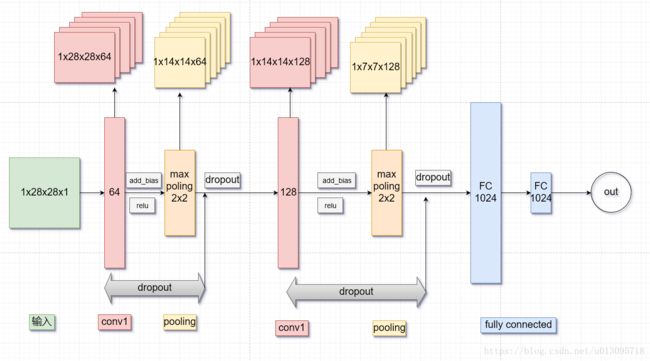
下面以本例代码为例,讲解本例的网络结构。网络总体结构如下
1. 输入层
维度: n×784 n × 784
这里n表示的样本数,784是一张图片的 width×height w i d t h × h e i g h t ,所得得总像素数目。即图像得数据向量。但是由于卷积利用得是原始图像矩阵,故需要一个reshape操作,将图片reshape成原始得 28×28×1 28 × 28 × 1 的形式。
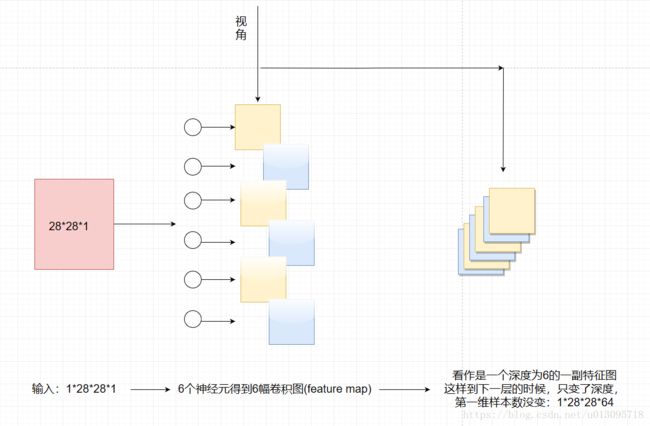
这个1需要重点理解以下,它表示数据的深度,在输入数据上,表示的是图像的通道,通常彩色图像是3或者4(多了一个透明度alpha)通道(channel),而本文所用的图片都是灰度图,只有一个通道,即深度为1。如下图所示
故我们将reshape操作后的数据看作输入层的输出(怪怪的,懂这个意思就是了,反正就是进入卷积网络的数据)
维度: n×28×28×1 n × 28 × 28 × 1
之后的层中我们将忽略这个n(这个n通常是一个batch_size,因为送入网络的通常是一批样本数据,而不是整个训练集),只关注一个样本在网络中的流动。
2.第一个卷积层conv1
input: 1×28×28×1 1 × 28 × 28 × 1 ,size是 28×28 28 × 28
kernel:卷积模板, 3×3×1 3 × 3 × 1 ,分别是长,宽,深(depth,channel)
neuron:神经元个数,64个。此处需要理解,一个神经元对图像进行一趟完整的卷积(即卷积模板扫过图像的所有像素),得到1个卷积结果图(结果也是矩阵)。
out:由neuron得出,输出是64个卷积结果图(称之为特征图,feature map)
parameter:上述分析,可得conv1的卷积参数 28×28×1×64 28 × 28 × 1 × 64
strides:卷积过程中,描述模板窗口滑动的参数,通常设置为
strides = [1, stride, stride, 1],stride为水平和垂直的kernel滑动步长。padding:卷积操作会遇到边缘问题(模板移出图像边界),此处需要添加边缘(在外层套一层像素点),增加像素点的策略,内置了两种,’SAME’,表示边缘填充0,’VALID’,表示边缘如果不够一次卷积操作,就是说需要增加边缘像素那么就放弃这一次卷积,进入下一行进行卷积操作。
out_size:这里指单个neuron得到的卷积图像的尺寸,通过input_size 、kernel_size、strides计算得 28×28 28 × 28 ,由于padding设置了添加’SAME’,会进行边缘填充,故尺寸不会变化。
code:
w_conv1 = tf.Variable(tf.random_normal([3, 3, 1, 64], stddev=std))conv1 = tf.nn.conv2d(_x, w_conv1, strides=[1, 1, 1, 1], padding='SAME')
3.第一个池化层
通常,一个卷积层之后会接一个池化层,池化的理解就是下采样(downsample),个人理解池化有以下作用
- 降低数据规模
- 模拟认知的抽象,即精细的高分辨率细节向高层模糊,然后通过后续卷积提取高层语义特征。
- 实现尺度变换,让各卷积层提取的特征存在尺度上的差异。(这一点在FPN中被用到,但FPN还存在top-down的连接暂且不说)
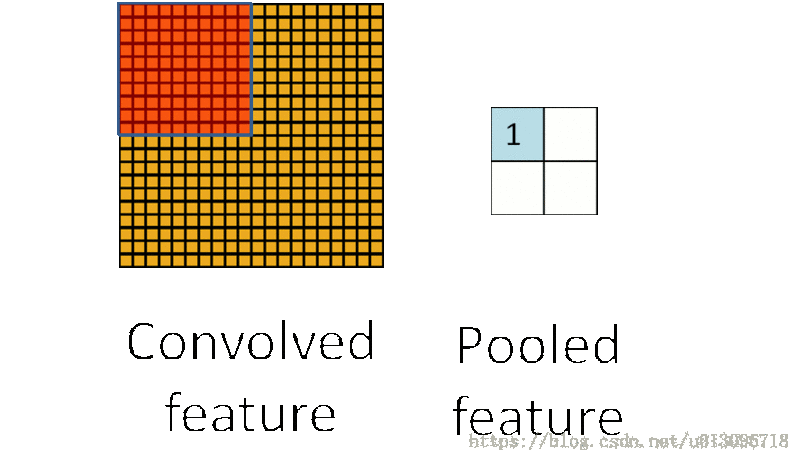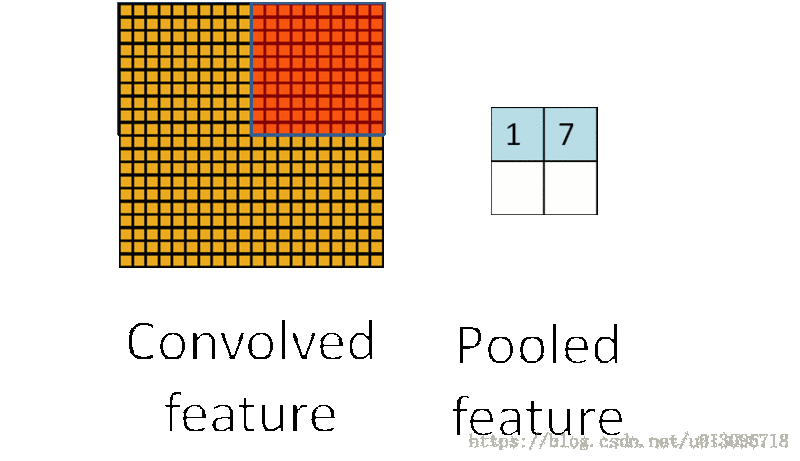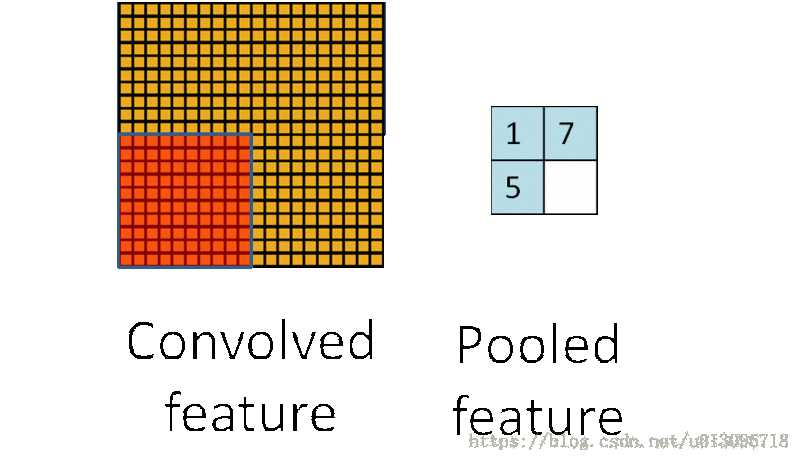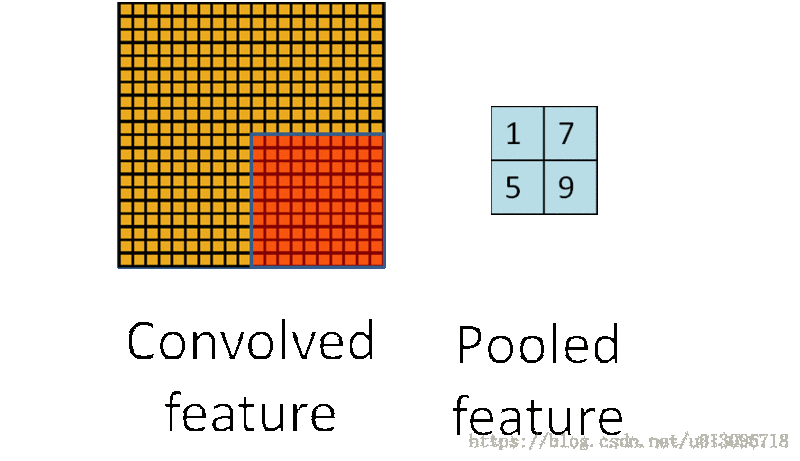
事实上,卷积层也具有上述两个功能(尺寸是否变化得看padding策略,通常为了方便计算尺寸参数,建议采用’SAME’策略),但不同的是,卷积层通过卷积(线性叠加)操作具有了提取特征的能力,可以理解为pooling是为了卷积层服务的。Pooling的图示如下(显然池化层会改变尺寸!)
常见的池化方式(采样方式)
- 均值采样,mean-pooling,计算图像被kernel覆盖区域的平均值作为该区域池化后对应的一个像素的值。
- 最大值采用,max-pooling,计算图像被kernel覆盖区域的最大值作为该区域池化后对应的一个像素的值。
本例中的池化层1,pool1
- input: 1×28×28×64 1 × 28 × 28 × 64
- policy:max-pooling
- parameter:
ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME',即采样是4个点取一个最大值点,步长也是[2,2],说明kernel不会重叠,padding采用边缘超出时补0的策略 - out: 1×14×14×64 1 × 14 × 14 × 64
- size:从 28×28 28 × 28 变到 14×14 14 × 14
4. 第二个卷积层
- input: 1×14×14×64 1 × 14 × 14 × 64
- neuron:128
- out: 1×14×14×128 1 × 14 × 14 × 128 ,得到深度(也称为channel)为128的特征图
- size: 14×14 14 × 14 ,不变
5.第二个池化层
- input: 1×14×14×128 1 × 14 × 14 × 128
- policy:max-pooling
- parameter:
ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME' - out: 1×7×7×128 1 × 7 × 7 × 128
- size:从 14×14 14 × 14 变到 7×7 7 × 7
至此,通过两个卷积层(包括其后接的pooling和dropout),从原图得到了深度为128的 7×7 7 × 7 的特征图,之后需要将这个所得的特征图,reshape成特征向量,然后进行分类任务,做分类任务的时候,可以用神经网络方法,也可以用其他机器学习方法,本例用的神经网络算法,故reshape之后接了两层全连接层(这两层全连接层各有作用,下文说明)。
1*7*7*128 reshape 1*6272*1 #这里第一个维度表示的样本数,此出为1,表示一个样本
feature_vector = tf.reshape(conv2_out, [-1,_w['w_fc1'].get_shape().as_list()[0]])
6.第一层全连接
深层网络和浅层网络相比有什么优势呢?
简单来说深层网络能够表达力更强。事实上,一个仅有一个隐藏层的神经网络就能拟合任何一个函数,但是它需要很多很多的神经元。而深层网络用少得多的神经元就能拟合同样的函数。也就是为了拟合一个函数,要么使用一个浅而宽的网络,要么使用一个深而窄的网络。而后者往往更节约资源。
但深层网络的缺点是,不太容易训练。
经验上,相比于浅层但多neuron网络,我们更倾向于使用少的neuron的多层网络。
上述理论和这里的第一个连接层的作用并没有特别大的关系,但是还是想提一下。本例中的第一层全连接什么作用呢?
我认为,最主要的作用就是降维:图像得到的特征向量有6272维,这里我们通过第一层全连接,降到1024维。
- input: 1×6272×1 1 × 6272 × 1
- neuron:1024个,全连接神经元,即和所有的输入数据按权值相连。
- out: 1×1024×1 1 × 1024 × 1
- code:
w_fc1 = tf.Variable(tf.random_normal([7 * 7 * 128, 1024], stddev=std))
fc1 = tf.nn.relu(tf.add(tf.matmul(feature_vector, w_fc1, b_fc1)) # relu激活函数
7.第二层全连接
这一层全连接,直接输出分类结果,可以在后面添加softmax层,输出个分类的得分(概率),然后loss 使用logistic loss,当然,这等效于不加softmax,但后续的cost function用softmax_cross_entropy_with_logits,代码如下(事实上,logistic loss 和 cross entropy loss 殊途同归)
# 代码引用自:http://blog.csdn.net/caimouse
import tensorflow as tf
#our NN's output
logits = tf.constant([[1.0,2.0,3.0],[1.0,2.0,3.0],[1.0,2.0,3.0]])
#step1:do softmax
y = tf.nn.softmax(logits)
#true label
y_ = tf.constant([[0.0,0.0,1.0],[0.0,0.0,1.0],[0.0,0.0,1.0]])
#step2:do cross_entropy
cross_entropy = -tf.reduce_sum(y_*tf.log(y))
#do cross_entropy just one step
cross_entropy2 = tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=y_))
with tf.Session() as sess:
softmax=sess.run(y)
c_e = sess.run(cross_entropy)
c_e2 = sess.run(cross_entropy2)
print("step1:softmax result=")
print(softmax)
print("step2:cross_entropy result=")
print(c_e)
print("Function(softmax_cross_entropy_with_logits) result=")
print(c_e2)
# 输出
'''
step1:softmax result=
[[ 0.09003057 0.24472848 0.66524094]
[ 0.09003057 0.24472848 0.66524094]
[ 0.09003057 0.24472848 0.66524094]]
step2:cross_entropy result=
1.22282
Function(softmax_cross_entropy_with_logits) result=
1.22282
'''上述代码来自:caimouse的博客
本例的第二层全连接用于输出分类,具体细节如下
- input: 1×1024×1 1 × 1024 × 1
- neuron:10个,全连接神经元,输出对应到10个分类的得分。
- out: 1×10×1 1 × 10 × 1
- code:
w_fc2 = tf.Variable(tf.random_normal([1024, 10], stddev=std))
out = tf.add(tf.matmul(fc1_out, w_fc2), b_fc2) # 输出层不用激活
至此,本例的网络结构分析完毕,下面上代码
# -*- coding: utf-8 -*-
# @File : 5_CNN_MINIST.py
# @Time : 2018/5/29 20:49
# @Author : hyfine
# @Contact : [email protected]
# @Desc : 建立简单的卷积神经网络结构,实现手写体的识别
import input_data
import cv2
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# 数据集合
def load_dataset():
print('------------ DATA LOADING ------------')
# minist数据集采用tensorflow自带的加载脚本input_data.py加载
minist = input_data.read_data_sets('data/', one_hot=True)
# 训练集55000,验证集5000,测试集10000
# 模型训练的时候,验证集全部输入,我显卡会OOM,所以只用了前1000张做准确率的测试
# 测试的时候,没有采用数据集自带的sample,而是自己预处理了手写的数据用于测试
print("train shape:", minist.train.images.shape, minist.train.labels.shape)
print("test shape:", minist.test.images.shape, minist.test.labels.shape)
print("valid shape:", minist.validation.images.shape, minist.validation.labels.shape)
print("----------MNIST loaded----------------")
return {'train': minist.train, 'test': minist.test, 'valid': minist.validation}
# 定义网络结构,预定义网络参数
def net_params():
# 网络中的参数(输入,输出,权重,偏置)
n_input = 784
n_out = 10
# 标准差
std = 0.1
w = {
'w_conv1': tf.Variable(tf.random_normal([3, 3, 1, 64], stddev=std)),
'w_conv2': tf.Variable(tf.random_normal([3, 3, 64, 128], stddev=std)),
# 此处的7*7是前两层卷积池化之后的尺寸,是通过网络结构参数,计算出来的
'w_fc1': tf.Variable(tf.random_normal([7 * 7 * 128, 1024], stddev=std)),
'w_fc2': tf.Variable(tf.random_normal([1024, n_out], stddev=std))
}
b = {
'b_conv1': tf.Variable(tf.zeros([64])),
'b_conv2': tf.Variable(tf.zeros([128])),
'b_fc1': tf.Variable(tf.zeros([1024])),
'b_fc2': tf.Variable([tf.zeros([n_out])])
}
print('-------------- CNN_NET READY! --------------')
return {'input_len': n_input, 'output_len': n_out, 'weight': w, 'bias': b}
# 前向传播过程。(各网络层的连接)
def forward_propagation(_x, _w, _b, _keep_ratio):
# 1.将输入x向量矩阵化,因为卷积要在图像矩阵上操作
_x = tf.reshape(_x, [-1, 28, 28, 1])
# 2.第一个卷积+池化+dropout
conv1 = tf.nn.conv2d(_x, _w['w_conv1'], strides=[1, 1, 1, 1], padding='SAME')
# 输出归一化(保证下一层的输入数据是经过归一化的)
# _mean, _var = tf.nn.moments(conv1, [0, 1, 2])
# conv1 = tf.nn.batch_normalization(conv1, _mean, _var, 0, 1, 0.0001)
# 激活函数,activation
conv1 = tf.nn.relu(tf.nn.bias_add(conv1, _b['b_conv1']))
# 推荐数据流动过程中查看shape变化情况
print('conv1:', conv1.shape)
# 池化
pool1 = tf.nn.max_pool(conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
print('pool1:', pool1.shape)
# 失活,dropout
out_conv1 = tf.nn.dropout(pool1, _keep_ratio)
# 3.第二个卷积+池化+dropout
conv2 = tf.nn.conv2d(out_conv1, _w['w_conv2'], strides=[1, 1, 1, 1], padding='SAME')
# _mean, _var = tf.nn.moments(conv1, [0, 1, 2])
# conv1 = tf.nn.batch_normalization(conv1, _mean, _var, 0, 1, 0.0001)
# 激活函数,activation
conv2 = tf.nn.relu(tf.nn.bias_add(conv2, _b['b_conv2']))
print('conv2:', conv2.shape)
# 池化
pool2 = tf.nn.max_pool(conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
print('pool2:', pool2.shape)
# 失活,dropout
out_conv2 = tf.nn.dropout(pool2, _keep_ratio)
# 4.向量化,之后的全连接的输入应该是一个样本的特征向量
feature_vector = tf.reshape(out_conv2, [-1, _w['w_fc1'].get_shape().as_list()[0]])
print('feature_vector:', feature_vector.shape)
# 5.第一个 full connected layer,特征向量降维
fc1 = tf.nn.relu(tf.add(tf.matmul(feature_vector, _w['w_fc1']), _b['b_fc1']))
fc1_do = tf.nn.dropout(fc1, _keep_ratio)
print('fc1:', fc1.shape)
# 6.第二个 full connected layer,分类器
out = tf.add(tf.matmul(fc1_do, _w['w_fc2']), _b['b_fc2'])
print('fc2:', out.shape)
return out
# 训练过程
def training(train, valid):
# 先得到网络参数
params = net_params()
n_input = params['input_len']
n_out = params['output_len']
w = params['weight']
b = params['bias']
keep_ratio = tf.placeholder(tf.float32)
# 输入数据,及其对应的真实labels,这里用placeholder占位
x = tf.placeholder(tf.float32, [None, n_input])
y = tf.placeholder(tf.float32, [None, n_out])
y_ = forward_propagation(x, w, b, keep_ratio)
# 训练任务:优化求解最小化cost
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=y_, labels=y))
lr = 0.01
optm = tf.train.AdamOptimizer(lr).minimize(cost)
# 计算准确率,用以衡量模型
result_bool = tf.equal(tf.argmax(y_, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(result_bool, tf.float32))
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
print('------- Start Training! ----------')
# 训练参数
epochs = 20
display_step = 1
# 本人是cpu版本tensorflow,全部样本训练太慢,这里选用部分数据,且batch_size也较小
batch_size = 200
# batch_count = 100
batch_count = int(train.num_examples / batch_size)
for epoch in range(epochs):
avg_cost = 0.
batch_x, batch_y = None, None
# 分批次进行最小化loss的训练过程
for batch_index in range(batch_count):
batch_x, batch_y = train.next_batch(batch_size)
feeds = {x: batch_x, y: batch_y, keep_ratio: 0.6}
sess.run(optm, feed_dict=feeds)
avg_cost += sess.run(cost, feed_dict=feeds)
avg_cost /= batch_count
# 检查当前模型的准确率,查看拟合情况
if epoch % display_step == display_step - 1:
feed_train = {x: batch_x, y: batch_y, keep_ratio: 1}
# 全部的验证集都会OOM,所以只取前1000张
feed_valid = {x: valid.images[:1000], y: valid.labels[:1000], keep_ratio: 1}
ac_train = sess.run(accuracy, feed_dict=feed_train)
ac_valid = sess.run(accuracy, feed_dict=feed_valid)
print('Epoch: %03d/%03d cost: %.5f train_accuray:%0.5f valid_accuray:%0.5f' % (
epoch + 1, epochs, avg_cost, ac_train, ac_valid))
print('------- TRAINING COMPLETE ------------')
# 保存模型
saver = tf.train.Saver()
# 这里后缀名ckpt,表示checkpoint,这个可以任意
save_path = saver.save(sess, 'model/cnn_mnist_model.ckpt')
print(save_path)
print('------ MODEL SAVED --------------')
def image_preprocess(file_path: str):
"""
读取图片并返回图片的预处理之后的数据,预处理包括(resize、reshape、threshold)
:param file_path: 图片的地址
:return: numpy.ndarray类型的数据预处理之后的数据
"""
image = cv2.imread(file_path, cv2.IMREAD_GRAYSCALE)
# 默认双线性插值resize
image = cv2.resize(image, (28, 28))
# 二值化
ret, image = cv2.threshold(image, 127, 255, cv2.THRESH_BINARY_INV)
# 为了强化图像,再进行腐蚀和膨胀操作(这里因为经过反向二值化,应该做闭操作)
# kernel = np.ones((5, 5), np.uint8)
# image = cv2.morphologyEx(image, cv2.MORPH_CLOSE, kernel)
# 显示图片(查看二值效果)
# plt.imshow(image)
# plt.show()
# 归一化
image = image / 255.
image = image.astype(np.float32)
return np.reshape(image, [1, 784])
def test():
# 先得到网络参数
params = net_params()
n_input = params['input_len']
n_out = params['output_len']
w = params['weight']
b = params['bias']
keep_ratio = tf.placeholder(tf.float32)
x = tf.placeholder(tf.float32, [None, n_input])
y = tf.placeholder(tf.float32, [None, n_out])
y_ = forward_propagation(x, w, b, keep_ratio)
# 求具体的分类结果
result = tf.argmax(tf.nn.softmax(y_), 1)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
# 加载模型
saver = tf.train.Saver()
saver.restore(sess, 'model/cnn_mnist_model.ckpt')
print('---------- Model restored! ------------')
# 进行测试
print('---------- TESTING ---------------------')
# 输入图像
img_path = 'data/mini_test_2_original.png'
test_2 = image_preprocess(img_path)
img_path = 'data/mini_test_3_original.png'
test_3 = image_preprocess(img_path)
img_path = 'data/mini_test_7_original.png'
test_7 = image_preprocess(img_path)
img_path = 'data/mini_test_8.png'
test_8 = image_preprocess(img_path)
# 组成输入矩阵
test_input = np.vstack((test_2, test_3, test_7, test_8))
# 输入网络计算
feed_test = {x: test_input, keep_ratio: 1}
result = sess.run(result, feed_dict=feed_test)
print('------------ 测试结果 --------------')
for i, v in enumerate(result):
print('第%d个输入的是:%d' % (i + 1, v))
# 查看具体的得分情况
print(sess.run(y_, feed_dict=feed_test))
if __name__ == '__main__':
#data_set = load_dataset()
#training(data_set['train'], data_set['valid'])
test()输出结果