线性代数：矩阵变换图形（三维平移缩放旋转）

        紧接上一篇：http://blog.csdn.net/yinhun2012/article/details/79544205

        这篇博文我只是准备对上一篇博文的内容进行扩展，因为上一篇我写完二维xy仿射坐标系的变换，这一篇我就扩充到三维xyz仿射坐标系的变换推导。

        前面我们已经理解学习完矩阵在图形学中的作用，所以这一篇我只做纯推导和图形应用演示。

        1.矩阵操作三维仿射坐标系平移，如下图：

        

        三维仿射空间平移无非就是xyz三轴移动，建立齐次坐标和4x4矩阵就能推出来了。

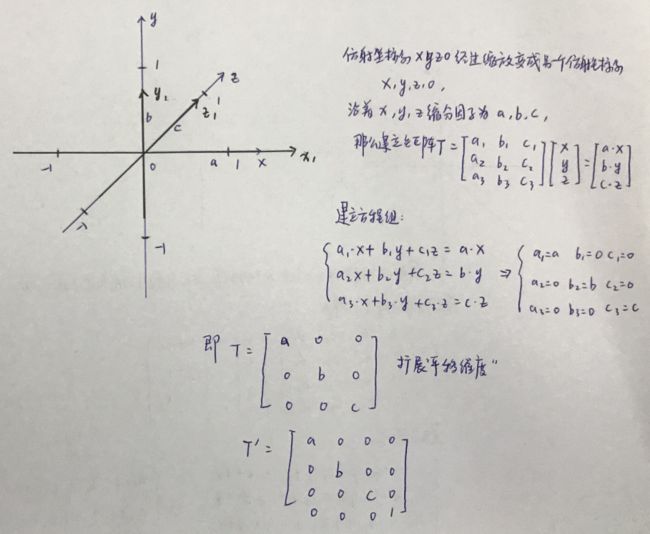
        2.矩阵操作三维仿射坐标系缩放，如下图：

        

            缩放也很简单，无非就是xyz轴缩放因子abc带入矩阵方程组计算得出。

            3.矩阵操作三维仿射坐标系旋转。

            三维下的旋转就会复杂一些，不同于二维坐标系旋转只能绕着那个不存在的Z轴正反旋转（或者说我们在纸上画一个XYZ三维仿射坐标系，但是Z轴垂直于纸面我们看不到，那么以XY为坐标轴的二维坐标系就只能绕着Z轴旋转，因为我们习惯性把旋转角按逆时针标记（三角函数中规定逆时针旋转为正角），这个前面我们讨论三角函数说过了，所以顺时针旋转我们也能通过转换得到逆时针旋转的θ角度值，那么也就是说XY二维坐标系的旋转就是绕着Z轴逆时针旋转），此时三维XYZ坐标系的旋转就变成了XY绕着Z逆时针旋转，XZ绕着Y逆时针旋转，YZ绕着X逆时针旋转，现在我们依次来推导：

            ①XY绕Z轴逆时针旋转，如下图：

            

这里我们依旧是建立3x3矩阵T和已知量来解线性方程组。

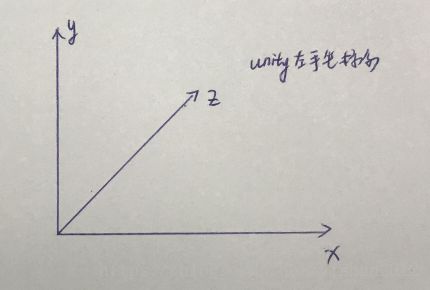
            ①XZ绕Y轴逆时针旋转，这个时候就要注意了，因为图形学有左右手坐标系之分，简单来说就是Z轴是向内还是向外的区别，我们可以观察得到unity的坐标系是左手坐标系，也就是Z轴向内，如下图：

            

            那么我们建立矩阵和已知量的推导就变成如下图：

            

            ①YZ绕X轴逆时针旋转，如下图：

            

        推导比较简单所以我直接发简写了，小伙伴可以自己绘画推导一下。

        讲了这么多，那么接下来就进入图形学程序的测试了，毕竟搞了一堆纸面知识，要是不应用到图形学程序上，那岂不是“纸上谈兵”，如下图：

        

下面是为测试图形变换所写的cgshader，这里我解释一下，仿射坐标系是一个抽象概念性质的东西，我们无法直接写代码使用matrix变换仿射坐标系，但是我们可以变通一下，写cg代码控制仿射坐标系原点所在的图形的每个顶点进行变换，这样同样达到矩阵变换的目的（注意程序中角度值一般都是使用弧度值进行计算的，在unity中你需要将degree2radian后进行参数传递）

        

Shader "Unlit/TransformationUnlitShader"
{
	Properties
	{
		_MainTex ("Texture", 2D) = "white" {}
		_T_xyz("XYZ_Translation",vector) = (0,0,0,1)
		_S_xyz("XYZ_Scale",vector) = (0,0,0,1)
		_R_xyz("XYZ_Rotate",vector) = (0,0,0,1)
	}
	SubShader
	{
		Tags { "RenderType"="Opaque" }
		LOD 100

		Pass
		{
			CGPROGRAM
			#pragma vertex vert
			#pragma fragment frag
			
			#include "UnityCG.cginc"

			struct appdata
			{
				float4 vertex : POSITION;
				float2 uv : TEXCOORD0;
			};

			struct v2f
			{
				float2 uv : TEXCOORD0;
				float4 vertex : SV_POSITION;
			};

			sampler2D _MainTex;
			float4 _MainTex_ST;
			vector _T_xyz;  //xyz轴移动量
			vector _S_xyz;  //xyz轴缩放量
			vector _R_xyz;  //xyz轴旋转量，分量数值为角度值
			
			v2f vert (appdata v)
			{
				v2f o;
				//构建平移矩阵
				float4x4 _Mat_T = float4x4(1,0,0,_T_xyz.x,
											0,1,0,_T_xyz.y,
											0,0,1,_T_xyz.z,
											0,0,0,1);
				//构建缩放矩阵
				float4x4 _Mat_S = float4x4(_S_xyz.x,0,0,0,
											0,_S_xyz.y,0,0,
											0,0,_S_xyz.z,0,
											0,0,0,1);
				//构建旋转矩阵

				//x轴旋转  
				float4x4 _Mat_R_x = float4x4(1, 0, 0, 0,
											0, cos(_R_xyz.x), -sin(_R_xyz.x), 0,
											0, sin(_R_xyz.x), cos(_R_xyz.x), 0,
											0, 0, 0, 1);
				//y轴旋转  
				float4x4 _Mat_R_y = float4x4(cos(_R_xyz.y), 0, sin(_R_xyz.y), 0,
											0, 1, 0, 0,
											-sin(_R_xyz.y), 0, cos(_R_xyz.y), 0,
											0, 0, 0, 1);
				//z轴旋转  
				float4x4 _Mat_R_z = float4x4(cos(_R_xyz.z), -sin(_R_xyz.z), 0, 0,
											sin(_R_xyz.z), cos(_R_xyz.z), 0, 0,
											0, 0, 1, 0,
											0, 0, 0, 1);
				//首先我们平移
				float4 vx = mul(_Mat_T,v.vertex);  //mul为矩阵乘法，vertex为模型的网格坐标点
				//然后我们缩放
				vx = mul(_Mat_S, vx);
				//然后我们旋转
				vx = mul(_Mat_R_x, vx);
				vx = mul(_Mat_R_y, vx);
				vx = mul(_Mat_R_z, vx);
				//vx = mul(_Mat_R_z,mul(_Mat_R_y,mul(_Mat_R_x,vx)));  //或者直接写成这种形式
				o.vertex = UnityObjectToClipPos(vx);
				o.uv = TRANSFORM_TEX(v.uv, _MainTex);
				return o;
			}
			
			fixed4 frag (v2f i) : SV_Target
			{
				fixed4 col = tex2D(_MainTex, i.uv);
				return col;
			}
			ENDCG
		}
	}
}

 

 

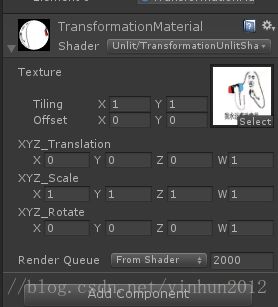
         shader代码中vertex顶点函数中，构建了平移，缩放，旋转的矩阵，参数由外部vector传递，如下图：

 

 

        然后写好c#外部参数控制脚本

        

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class TransformationCtrl : MonoBehaviour
{

    public Renderer mRender;
    public bool bTranslate;
    public bool bScale;
    public bool bRotate;

    private Material mMat;

    private Vector4 mTranslate;
    private Vector4 mScale;
    private Vector4 mRotate;

    private float mTime;

    void Awake()
    {
        mMat = mRender.material;
    }

    void Start()
    {

    }

    void Update()
    {
        //平移
        if (bTranslate)
        {
            mTime += Time.deltaTime;
            if (mTime < 5.0f)
            {
                mTranslate = new Vector4(1.0f * mTime, 0.5f * mTime, 1.5f * mTime, 1);
                mMat.SetVector("_T_xyz", mTranslate);
            }
            else
            {
                mMat.SetVector("_T_xyz", new Vector4(0, 0, 0, 1));
                mTime = 0.0f;
                bTranslate = false;
            }
        }
        //缩放
        if (bScale)
        {
            mTime += Time.deltaTime;
            if (mTime < 5.0f)
            {
                mScale = new Vector4(4.0f * mTime / 5.0f + 1, 2.0f * mTime / 5.0f + 1, 1.0f * mTime / 5.0f + 1, 1);
                mMat.SetVector("_S_xyz", mScale);
            }
            else
            {
                mMat.SetVector("_S_xyz", new Vector4(1, 1, 1, 1));
                mTime = 0.0f;
                bScale = false;
            }
        }
        //旋转
        if (bRotate)
        {
            mTime += Time.deltaTime;
            if (mTime < 5.0f)
            {
                mRotate = new Vector4(720.0f * mTime / 5.0f * Mathf.Deg2Rad, 1080.0f * mTime / 5.0f * Mathf.Deg2Rad, 360.0f * mTime / 5.0f * Mathf.Deg2Rad, 1);
                mMat.SetVector("_R_xyz", mRotate);
            }
            else
            {
                mMat.SetVector("_R_xyz", new Vector4(0, 0, 0, 1));
                mTime = 0.0f;
                bRotate = false;
            }
        }
    }
}

 

        简单的update动画，但是形象的演示了matrix用于图形变换的计算。

 

        可能有小伙伴目前不懂cgshader，不要急，我们学习完基本数学博客后，立马就会进入C for Graphic和图形学理论，这里我们只是验证一下matrix在图形变换的作用。