一、编译器构造一般原理
一、编译器概述
1.翻译器（translator）：把一种语言程序翻译成另一种语言程序。
2.编译器（compiler）：高级语言变成低级语言。
3.解释器（interpreter）：将语句一条一条直接执行，而不生成目标代码。
4.编译器阶段：源程序->词法分析->语法分析->语义分析->中间代码生成器->独立于机器代码优化器->代码生成器->依赖于机器代码优化器。
5.词法分析器（lexical analysis，scanner）：
将字符序列转化为单词序列（token）的过程，如将position=initial+rate*60转化，通过词法分析器转化为如下
6.语法分析器（syntactic analysis，parser）：
将position=initial+rate*60经过词法分析得到的序列构造成一棵分析树（parse tree），如下
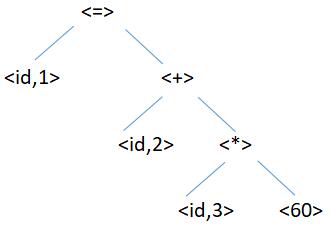符号表：1.position，2.initial，3.rate ...（也包含类型信息）
7.语义分析器（semantic analysis）：
输入语法树，输出也是语法树，收集标识符种属、类型、存储位置长度、值、参数返回等信息，存到符号表中，并进行语义检查。
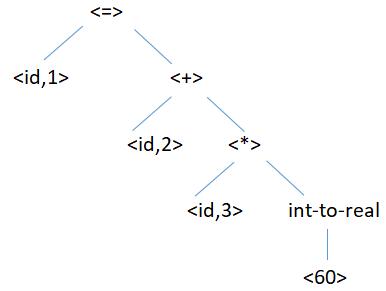
8.中间代码生成器（intermediate code generator）：将上述语法树生成中间代码如下（三地址指令）
t1=int-to-real(60)
t2=id3*t1
t3=id2+t2
id1=t3
9.代码优化器（code optimizer）：中间代码优化器可得到如下
t1=id3*60.0
id1=id2+t1
10.代码生成器（code generator）：生成汇编代码或机器码。
11.词法分析器与语法分析器关系：语法分析器作为主程序，调用词法分析器取下一个token，词法分析器取好返回给语法分析器，在这个过程期间它们都要访问符号表。（语法分析器后面还可能会调用语义分析器）
二、词法基本概念
1.字母表（alphabet）：表示字母的集合，记号为Σ，若Σ={0,1}则字母表中只有0或1。
2.字母表乘积（product）：Σ1Σ2=Σ3，则Σ3中存在两个字母，前一个字母在Σ1集合中，后一个字母在Σ2集合中。
3.字母表的幂（power）：字母表的n次幂表示长度为n的符号串构成的集合，这些符号在字母表集合内。
4.字母表闭包（closure）：由字母表中字母构成的所有串（包括空串），若为正（positive）闭包则不包含空串。
5.串（string）：符号的有穷序列，空串记为ε，通常用|s|记作串s的长度。
6.串的连接（concatenation）：如xy连接aa就等于xyaa，即追加串。
7.串的幂：(ab)^3=ababab，任何串0次幂为ε。
8.串的闭包：(ab)*为{ε,ab,abab,ababab,abababab,......}即(ab)^0并(ab)^1并...，若为正闭包则去掉空串。
9.语言（language）：字母表上的一个串集，如{ε,0,00,000}或者Ø。
10.语言的并运算：L∪M=结合了两种语言的语言。
11.语言的连接运算：LM=每一个句子的前一部分一定属于L语言，后一部分一定属于M语言。
12.语言的幂：L^0={ε}，L^i为语言所有句子的i次连接。
13.语言的闭包：L*=L^0并L^1并L^2并....，若正闭包则去掉L^0。
三、文法基本概念
1.文法形式化定义：
G=(Vt,Vn,P,S)
Vt为终结符（terminal symbol）集合，终结符也称token。
Vn为非终结符（nonterminal）集合，非终结符是表示语法成分的符号。
P为产生式（production）集合，描述了将终结符和非终结符组合成串的方，形式为a → b，读作a定义为b，这里要求a必须包含至少一个非终结符。
S为开始符号（start symbol），表示该文法中最大的语法成分。
文法解决了无穷语言的有穷表示问题。
2.文法的例子：
G=( {id,+,*,(,)} ， {E} ， P ， E )
P={ E → E+E ， E → E*E ， E → (E) ， E → id }
3.产生式简写：a → b1，a → b2，a → b3 可简写为 a → b1 | b2 | b3 。
4.推导（derivations）：A → B，B → (id) 推导为 A → (id) ，将最大语法成分推导为终结符组成的串。
5.归约（reductions）：由上例，A → (id) 可归约为 A → B ，推导逆操作，将终结符组成的串归约为最大语法成分。
6.句型（sentential form）：一个句型可包含终结符，又可包含非终结符，也可能是空串。
7.句子（sentence）：不包含非终结符的句型。
8.文法分类：
0型文法（无限制文法）：任意a → b，a中至少包含1个非终结符，能力相当于图灵机。
1型文法（上下文有关文法）：0型文法基础上，任意a → b，|a| <= |b| （b不等于ε），如 aAb → axb 上下文有关。
2型文法（上下文无关文法，context-free grammar）：每个产生式左部必须是非终结符，A → b 。
3型文法（正则文法，regular grammar）：A → wB或A → w（右线性），A → Bw或A → w（左线性）。
9.上下文无关文法的分析树：
根为文法开始符号，内部结点为某产生式的左部，一个内部结点和儿子构成了某产生式，分析树是推导的图形化表示。
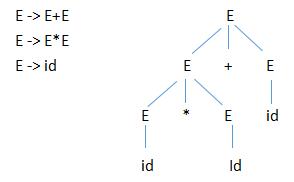分析树中根结点对应子树的边缘对应句型短语（phrase）本例 id*id+id 。
10.最左推导和最后推导（left/right-most derivation）：
例如给出如下产生式 E → E+E | E*E | (E) | -E | id
最左推导：推导过程中每次对最左边的非终结符展开。
E → -E → -(E) → -(E+E) → -(id+E) → -(id+id)
最右推导（规范推导）：每次对最右边的非终结符展开。
E → -E → -(E) → -(E+E) → -(E+id) → -(id+id)
注：最左推导和最右推导的分析树是一样的。
11.相同句子分析树的二义性（同为最左推导）：.
对于产生式 E → E+E | E*E | (E) | -E | id，要得到句子id*id+id，在最左推导的情况下，可以有这两种分析树。
为消除由运算优先级产生的二义性，可以这样定义文法
id*id*(id+id) + id*id + id 我们把加式连一块看作一个expr，把乘式连一块看作一个term。
id * id * (id+id) 连乘式中每一项看作一个因子factor。
文法就定义为：
expr → expr+term | term
term → term*factor | factor
factor → id | (expr)
例题1：
描述下述语言 L={(a^n) (d^m) (b^n)，n,m>=1}
解：
A → aAb | aBb 前面的aAb表示可一直延伸ab，即为 ...aaAbb... ，后面的aBb表示B可被d换
B → dB | d 即表示dd...
例题2：
证明下列文法是一个二义文法
A → B+B | B
B → B*B | A | a
解：
对于相同句子a+a*a，同是最左推导时，存在以下两个不同的分析树，因此为二义文法。
A → B+B → a+B → a+B*B → a+a*B → a+a*a
A → B → B*B → A*B → B+B*B → a+B*B → a+a*B → a+a*a