【TensorFlow学习笔记】进阶篇（二）卷积神经网络详解_MINIST实例（CNN_Lenet5）

绪论

在前一章中，我们学会了制作自己的数据集，不同于mnist数据集，我们自制的数据集图片是彩色图。
如果在全连接网络直接输入的是三通道的RGB彩色图片，待优化的参数过多容易导致模型过拟合，而且计算量过大。所以实际应用中会先对原始图像进行特征提取（卷积）再把提取到的特征喂给全连接网络，再让全连接网络进行参数优化，得到分类评估。这样可以减小计算量等。

卷积神经网络一般由卷积部分和全连接部分构成。卷积部分一般包含卷积（可以有多个不同尺寸的核级联组成）、池化、Dropout等，其中Dropout层必须放在池化之后。全连接部分一般最多包含2到3个全连接，最后通过Softmax得到分类结果。

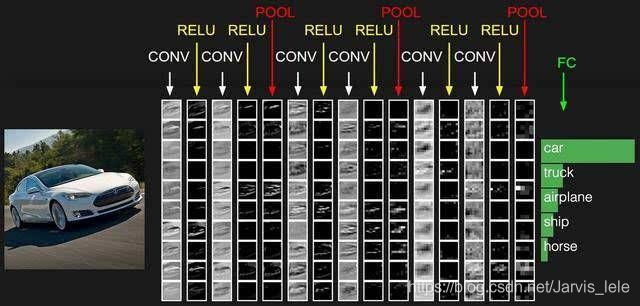
由于全连接层参数量大，现在倾向于尽可能的少用或者不用全连接层。神经网络的发展趋势是考虑使用更小的过滤器，如1x1,3x3等；网络的深度更深（2012年AlenNet8层，2014年VGG19层、GoogLeNet22层，2015年ResNet152层）；减少全连接层的使用，以及越来越复杂的网络结构，如GoogLeNet引入的Inception模块结构。CNN网络的发展历程如下图：

卷积神经网络架构的分析
白话CNN.

---

---

1. 全连接网络 VS 卷积网络

• 全连接网络

在前面的基础篇，我们运用了全连接网络来来进行MNIST数据集的分类，准确率最高可达98%。但是手写体图像相对来说较为简单，当进行较为复杂的图像识别分类时，全连接网络往往不能胜任，主要有以下几个方面的原因：

①参数数量太多

考虑一个输入10001000像素的图片(一百万像素，现在已经不能算大图了)，输入层有10001000=100万节点。假设第一个隐藏层有100个节点(这个数量并不多)，那么仅这一层就有(1000*1000+1)*100=1亿参数，这实在是太多了！我们看到图像只扩大一点，参数数量就会多很多，因此它的扩展性很差。

②没有利用像素之间的位置信息

对于图像识别任务来说，每个像素和其周围像素的联系是比较紧密的，和离得很远的像素的联系可能就很小了。如果一个神经元和上一层所有神经元相连，那么就相当于对于一个像素来说，把图像的所有像素都等同看待，这不符合前面的假设。当我们完成每个连接权重的学习之后，最终可能会发现，有大量的权重，它们的值都是很小的(也就是这些连接其实无关紧要)。努力学习大量并不重要的权重，这样的学习必将是非常低效的。

③网络层数限制

我们知道网络层数越多其表达能力越强，但是通过梯度下降方法训练深度全连接神经网络很困难，因为全连接神经网络的梯度很难传递超过3层。因此，我们不可能得到一个很深的全连接神经网络，也就限制了它的能力。

• 卷积网络

那么，卷积神经网络又是怎样解决这个问题的呢？主要有三个思路：

①局部连接

这个是最容易想到的，每个神经元不再和上一层的所有神经元相连，而只和一小部分神经元相连。这样就减少了很多参数。

②权值共享

一组连接可以共享同一个权重，而不是每个连接有一个不同的权重，这样又减少了很多参数。

③下采样

可以使用Pooling来减少每层的样本数，进一步减少参数数量，同时还可以提升模型的鲁棒性。

对于图像识别任务来说，卷积神经网络通过尽可能保留重要的参数，去掉大量不重要的参数，来达到更好的学习效果。接下来，我们将详述卷积神经网络到底是何方神圣。

2. 什么是卷积神经网络

初设卷积神经网络

我们先获取一个感性认识，下图是一个卷积神经网络的示意图：

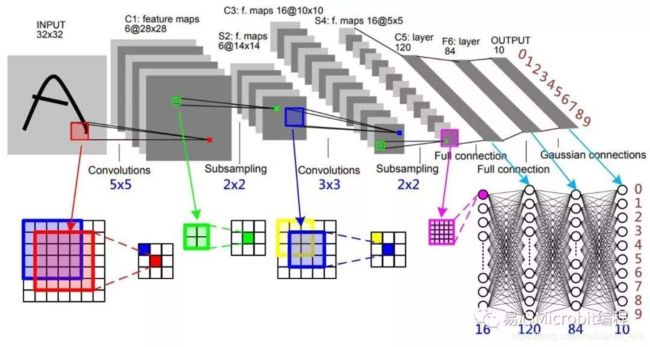
一幅图片进行卷积神经网络处理的过程。其中主要包含4个步骤：
（1）图像输入(input)：获取输入的数据图像。
（2）卷积（convolutions）：对图像特征进行提取。
（3）下采样（subsamping）：用于缩小在卷积时获取的图像特征。
（4）全连接层(full connection)：用于对图像进行分类。

从示意图我们可以发现卷积神经网络的层结构和全连接神经网络的层结构有很大不同。全连接神经网络每层的神经元是按照一维排列的，也就是排成一条线的样子；而卷积神经网络每层的神经元是按照三维排列的，也就是排成一个长方体的样子，有宽度、高度和深度。

对于示意图展示的神经网络，我们看到输入层的宽度和高度对应于输入图像的宽度和高度，而它的深度为1。接着，第一个卷积层对这幅图像进行了卷积操作(后面我们会讲如何计算卷积)，得到了6个Feature Map，实际上，就是这个卷积层包6个Filter，也就是6套参数，每个Filter都可以把原始输入图像卷积得到一个Feature Map，6个Filter就可以得到6个Feature Map。至于一个卷积层可以有多少个Filter，那是可以自由设定的。也就是说，卷积层的Filter个数也是一个超参数。我们可以把Feature Map可以看做是通过卷积变换提取到的图像特征，6个Filter就对原始图像提取出6组不同的特征，也就是得到了6个Feature Map，也称做6个通道(channel)。

继续观察示意图，在第一个卷积层之后，Pooling层对6个Feature Map做了下采样(后面我们会讲如何计算下采样)，得到了6个更小的Feature Map。接着，是第二个卷积层，它有16个Filter。每个Fitler都把前面下采样之后的6个Feature Map卷积在一起，得到一个新的Feature Map。这样，16个Filter就得到了16个Feature Map。接着，是第二个Pooling，继续对16个Feature Map进行下采样，得到了16个更小的Feature Map。

示意图所示网络的最后两层是全连接层。第一个全连接层的每个神经元，和上一层16个Feature Map中的每个神经元相连，第二个全连接层(也就是输出层)的每个神经元，则和第一个全连接层的每个神经元相连，这样得到了整个网络的输出。

至此，我们对卷积神经网络有了最基本的感性认识。接下来，我们将细致的介绍卷积神经网络的计算过程。

卷积神经网络输出值的计算

- 卷积层输出值的计算

我们用一个简单的例子来讲述如何计算卷积，然后，我们抽象出卷积层的一些重要概念和计算方法。
假设有一个5x5的图像，使用一个3x3的filter进行卷积，想得到一个3x3的Feature Map，如下所示：

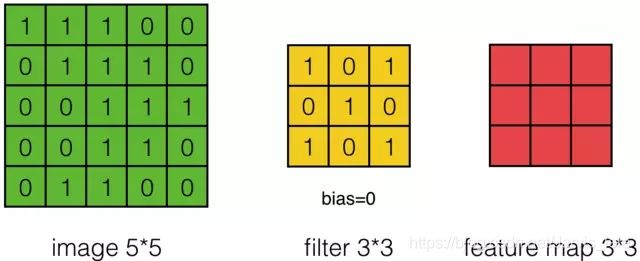
为了清楚的描述卷积计算过程，我们首先对图像的每个像素进行编号，用Xi,j表示图像的第行第列元素；对filter的每个权重进行编号，用Wm,n表示第m行第n列权重，用Wb表示filter的偏置项；对Feature Map的每个元素进行编号，用ai,j表示Feature Map的第i行第j列元素；用f表示激活函数(这个例子选择relu函数作为激活函数)。然后，使用下列公式计算卷积：

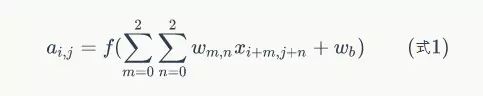
例如，对于Feature Map左上角元素来说，其卷积计算方法为：

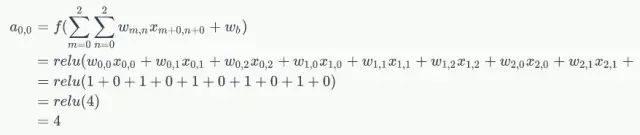
计算结果如下图所示：

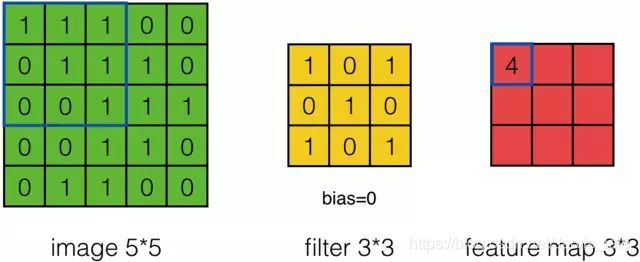
接下来，Feature Map的元素的卷积计算方法为：

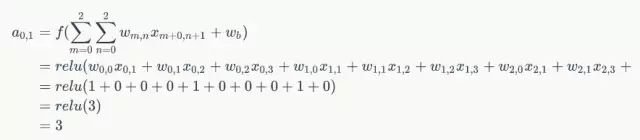
计算结果如下图所示：

可以依次计算出Feature Map中所有元素的值。下面的动画显示了整个Feature Map的计算过程：

上面的计算过程中，步幅(stride)为1。步幅可以设为大于1的数。例如，当步幅为2时，Feature Map计算如下：

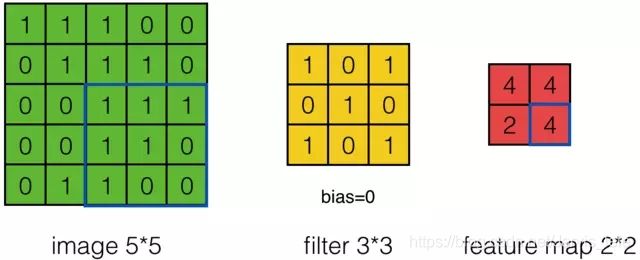
我们注意到，当步幅设置为2的时候，Feature Map就变成2x2了。

这说明图像大小、步幅和卷积后的Feature Map大小是有关系的。
卷积后所得feature map尺寸大小计算公式如下：：

像素宽度：W（Width）

填充大小：P（Padding）

卷积核大小：K（Kernel-size）

步长大小：S（stride）

补充：

1.Padding的作用用于解决图像边缘信息损失的问题；

2.计算卷积后map尺寸时若不为整数则向下取整，而计算pooling后尺寸时则向上取整。

在上面公式中，W2是卷积后Feature Map的宽度；W1是卷积前图像的宽度；F是filter的宽度；P是Zero Padding数量，Zero Padding是指在原始图像周围补几圈0，如果P的值是1，那么就补1圈0；S是步幅；H2是卷积后Feature Map的高度；H1是卷积前图像的宽度。式2和式3本质上是一样的。
以前面的例子来说，图像宽度W1=5，filter宽度F=3，Zero PaddingP=0，步幅S=2，则

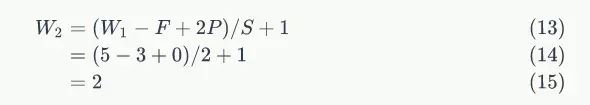
说明Feature Map宽度是2。同样，我们也可以计算出Feature Map高度也是2。

前面我们已经讲了深度为1的卷积层的计算方法，如果深度大于1怎么计算呢？其实也是类似的。如果卷积前的图像深度为D，那么相应的filter的深度也必须为D。我们扩展一下式1，得到了深度大于1的卷积计算公式：

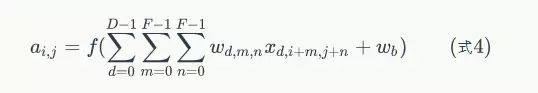
在式4中，D是深度；F是filter的大小(宽度或高度，两者相同)；Wd,m,n表示filter的第层第m行第n列权重；ad,I,j表示图像的第d层第i行第j列像素；其它的符号含义和式1是相同的，不再赘述。

我们前面还曾提到，每个卷积层可以有多个filter。每个filter和原始图像进行卷积后，都可以得到一个Feature Map。因此，卷积后Feature Map的深度(个数)和卷积层的filter个数是相同的。

下面的动画显示了包含两个filter的卷积层的计算。我们可以看到773输入，经过两个3x3x3filter的卷积(步幅为2)，得到了3x3x2的输出。另外我们也会看到下图的Zero padding是1，也就是在输入元素的周围补了一圈0。Zero padding对于图像边缘部分的特征提取是很有帮助的。
((5-3+2x1)/2+1=3)

以上就是卷积层的计算方法。这里面体现了局部连接和权值共享：每层神经元只和上一层部分神经元相连(卷积计算规则)，且filter的权值对于上一层所有神经元都是一样的。对于包含两个3x3x3的fitler的卷积层来说，其参数数量仅有(3x3x3+1)x2=56个，且参数数量与上一层神经元个数无关。与全连接神经网络相比，其参数数量大大减少了。

- Pooling层输出值的计算

Pooling层主要的作用是下采样，通过去掉Feature Map中不重要的样本，进一步减少参数数量。Pooling的方法很多，最常用的是Max Pooling。Max Pooling实际上就是在n*n的样本中取最大值，作为采样后的样本值。下图是2x2 max pooling：

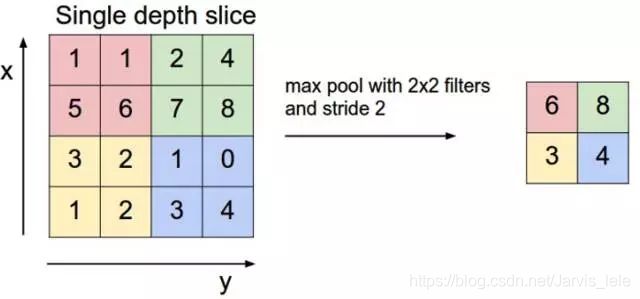
除了Max Pooing之外，常用的还有Mean Pooling——取各样本的平均值。

对于深度为D的Feature Map，各层独立做Pooling，因此Pooling后的深度仍然为D。

拓展：卷积核的大小

3. TensorFlow中卷积函数实现详解

- tf.get_variable函数

tf.get_variable(name,  shape, initializer):

• name就是变量的名称
• shape是变量的维度
• initializer是变量初始化的方式，初始化的方式有以下几种：

1. tf.constant_initializer：常量初始化函数
2. tf.random_normal_initializer：正态分布
3. tf.truncated_normal_initializer：截取的正态分布
4. tf.random_uniform_initializer：均匀分布
5. tf.zeros_initializer：全部是0
6. tf.ones_initializer：全是1
7. tf.uniform_unit_scaling_initializer：满足均匀分布，但不影响输出数量级的随机值

- tf.nn.conv2d卷积函数

tf.nn.conv2d(
    input,
    filter,
    strides,
    padding,
    use_cudnn_on_gpu=True,
    data_format='NHWC',
    dilations=[1, 1, 1, 1],
    name=None
)

这里核心的参数有5个，解释如下：
• input：指需要做卷积的输入图像，它要求是一个Tensor，具有[batch, in_height, in_width,in_channels]这样的shape，具体含义是[训练时一个batch的图片数量、图片高度、图片宽度、图像通道数]，注意这是一个四维的Tensor，要求类型为float32和float64其中之一。
• filter：相当于CNN中的卷积核，它要求是一个Tensor，具有[filter_height, filter_width,in_channels, out_channels]这样的shape，具体含义是[卷积核的高度、卷积核的宽度、图像通道数、卷积核个数]，要求类型与参数input相同，有一个地方需要注意，第三维in_channels，就是参数input的第四维。
• strides：卷积时在图像每一维的步长，这是一个一维的向量，第一维和第四维默认为1，而第三维和第四维分别是平行和竖直滑行的步进长度。
• padding：string类型的量，只能是“SAME”“VALID”其中之一，这个值决定了不同的卷积方式。
• use_cudnn_on_gpu：bool类型，是否使用cudnn加速，默认为true。

- tf.nn.max_pool池化函数

tf.nn.max_pool(
    value,
    ksize,
    strides,
    padding,
    data_format='NHWC',
    name=None
)

参数是4个，和卷积很类似，效果则如图13-4所示。
• value：需要池化的输入，一般池化层接在卷积层后面，所以输入通常是feature map，依然是[batch, height, width, channels]这样的shape。
• ksize：池化窗口的大小，取一个四维向量，一般是[1, height, width, 1]，因为我们不想在batch和channels上做池化，所以这两个维度设为了1。
• strides：和卷积类似，窗口在每一个维度上滑动的步长，一般也是[1, stride,stride, 1]。
• padding：和卷积类似，可以取‘VALID’或者‘SAME’，返回一个Tensor，类型不变，shape仍然是[batch, height, width, channels]这种形式。

4. MINIST实例（Lenet5）

• 经典的lenet5算法

[ 5 * 5 * 16]即为卷积神经网络提取的特征，将其作为输入喂给全连接网络。

• 使用MNIST数据集的lenet5算法

在这里插入图片描述
[7 * 7 * 64]即为卷积神经网络提取的特征，将其作为输入喂给全连接网络。

• mnist_Lenet_forward.py

#coding:utf-8
import tensorflow as tf
IMAGE_SIZE = 28
NUM_CHANNELS = 1
CONV1_SIZE = 5
CONV1_KERNEL_NUM = 32
CONV2_SIZE = 5
CONV2_KERNEL_NUM = 64
FC_SIZE = 512
OUTPUT_NODE = 10

def get_weight(shape, regularizer):
	w = tf.Variable(tf.truncated_normal(shape,stddev=0.1))
	if regularizer != None: tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w)) 
	return w

def get_bias(shape): 
	b = tf.Variable(tf.zeros(shape))  
	return b

def conv2d(x,w):  
	return tf.nn.conv2d(x, w, strides=[1, 1, 1, 1], padding='SAME')

def max_pool_2x2(x):  
	return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME') 

def forward(x, train, regularizer):
    conv1_w = get_weight([CONV1_SIZE, CONV1_SIZE, NUM_CHANNELS, CONV1_KERNEL_NUM], regularizer) 
    conv1_b = get_bias([CONV1_KERNEL_NUM]) 
    conv1 = conv2d(x, conv1_w) 
    relu1 = tf.nn.relu(tf.nn.bias_add(conv1, conv1_b)) 
    pool1 = max_pool_2x2(relu1) 

    conv2_w = get_weight([CONV2_SIZE, CONV2_SIZE, CONV1_KERNEL_NUM, CONV2_KERNEL_NUM],regularizer) 
    conv2_b = get_bias([CONV2_KERNEL_NUM])
    conv2 = conv2d(pool1, conv2_w) 
    relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_b))
    pool2 = max_pool_2x2(relu2)

    pool_shape = pool2.get_shape().as_list() 
    nodes = pool_shape[1] * pool_shape[2] * pool_shape[3] 
    reshaped = tf.reshape(pool2, [pool_shape[0], nodes]) 

    fc1_w = get_weight([nodes, FC_SIZE], regularizer) 
    fc1_b = get_bias([FC_SIZE]) 
    fc1 = tf.nn.relu(tf.matmul(reshaped, fc1_w) + fc1_b) 
    if train: fc1 = tf.nn.dropout(fc1, 0.5)

    fc2_w = get_weight([FC_SIZE, OUTPUT_NODE], regularizer)
    fc2_b = get_bias([OUTPUT_NODE])
    y = tf.matmul(fc1, fc2_w) + fc2_b
    return y 

• mnist_Lenet_backward.py

#coding:utf-8
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import mnist_lenet5_forward
import os
import numpy as np

BATCH_SIZE = 100
LEARNING_RATE_BASE =  0.005 
LEARNING_RATE_DECAY = 0.99 
REGULARIZER = 0.0001 
STEPS = 50000 
MOVING_AVERAGE_DECAY = 0.99 
MODEL_SAVE_PATH="./model/" 
MODEL_NAME="gesture_model"

def backward(mnist):
    x = tf.placeholder(tf.float32,[
	BATCH_SIZE,
	mnist_lenet5_forward.IMAGE_SIZE,
	mnist_lenet5_forward.IMAGE_SIZE,
	mnist_lenet5_forward.NUM_CHANNELS]) 
    y_ = tf.placeholder(tf.float32, [None, mnist_lenet5_forward.OUTPUT_NODE])
    y = mnist_lenet5_forward.forward(x,True, REGULARIZER) 
    global_step = tf.Variable(0, trainable=False) 

    ce = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
    cem = tf.reduce_mean(ce) 
    loss = cem + tf.add_n(tf.get_collection('losses')) 

    learning_rate = tf.train.exponential_decay( 
        LEARNING_RATE_BASE,
        global_step,
        mnist.train.num_examples / BATCH_SIZE, 
		LEARNING_RATE_DECAY,
        staircase=True) 
    
    train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)

    ema = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)
    ema_op = ema.apply(tf.trainable_variables())
    with tf.control_dependencies([train_step, ema_op]): 
        train_op = tf.no_op(name='train')

    saver = tf.train.Saver() 

    with tf.Session() as sess: 
        init_op = tf.global_variables_initializer() 
        sess.run(init_op) 

        ckpt = tf.train.get_checkpoint_state(MODEL_SAVE_PATH) 
        if ckpt and ckpt.model_checkpoint_path:
        	saver.restore(sess, ckpt.model_checkpoint_path) 

        for i in range(STEPS):
            xs, ys = mnist.train.next_batch(BATCH_SIZE) 
            reshaped_xs = np.reshape(xs,(  
		    BATCH_SIZE,
        	mnist_lenet5_forward.IMAGE_SIZE,
        	mnist_lenet5_forward.IMAGE_SIZE,
        	mnist_lenet5_forward.NUM_CHANNELS))
            _, loss_value, step = sess.run([train_op, loss, global_step], feed_dict={x: reshaped_xs, y_: ys}) 
            if i % 100 == 0: 
                print("After %d training step(s), loss on training batch is %g." % (step, loss_value))
                saver.save(sess, os.path.join(MODEL_SAVE_PATH, MODEL_NAME), global_step=global_step)

def main():
    mnist = input_data.read_data_sets("./data/", one_hot=True) 
    backward(mnist)

if __name__ == '__main__':
    main()