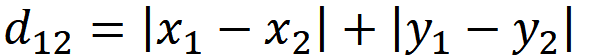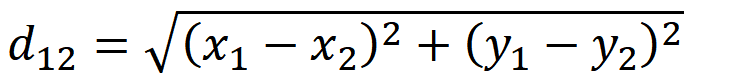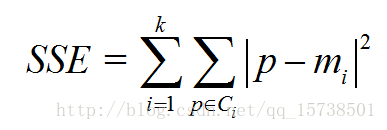聚类（二）——KMeans算法（工作面试常用面试题入手）

主要的KMeans算法的原理和应用，在学习典过程中，我们要带着以下几个问题去学习
以下问题摘自于https://blog.csdn.net/qq_33011855/article/details/81482511
1、简述一下K-means算法的原理和工作流程
2、K-means中常用的到中心距离的度量有哪些？
3、K-means中的k值如何选取?
4、K-means算法中初始点的选择对最终结果有影响吗？
5、K-means聚类中每个类别中心的初始点如何选择？
6、K-means中空聚类的处理
7、K-means是否会一直陷入选择质心的循环停不下来？
8、如何快速收敛数据量超大的K-means？
9、K-means算法的优点和缺点是什么？

一、原理和流程

1、原理

对给定的无标记的样本数据集，事先确定聚类簇数K，让簇内的样本尽可能紧密分布在一起，使簇间的距离尽可能大。K-Means作为无监督的聚类算法，其类似于全自动分类，簇内越相似，聚类效果越好，实现较简单，聚类效果好，因此被广泛使用。用以下的效果图更能直观地看出其过程：

2、流程

（1）随即确定K个初始点作为质心（这里如何确定k将在下面给出解释）
（2）将数据集中的每个点分配到一个簇中，即为每个点找距离其最近的质心，并将其分配给之心所对应的簇
（3）簇分好后，计算每个簇所有点的平均值，将平均值作为对应簇新的质心
（4）循环2、3步骤，直到质心不变

伪代码是：

创建k个点作为起始质心（经常是随机选择）
当任意一个点的簇分配结果发生改变时
	对数据集中的每个数据点
		对每个质心
			计算质心和数据点之间的距离
		将数据点分配到距离其最近的簇
	对每一个簇，计算簇中所有点的均值并将均值作为质心

上面“最近”质心，意味着需要进行某种距离的计算，即下文要介绍的K-means中常用的到中心距离的度量有哪些？

二、K-means中常用的到中心距离的度量有哪些

这里最常用的有以下两种（我们这里只简单介绍下二维的）

1、曼哈顿距离

2、欧几里得距离（别称“欧式距离”）

假如两个点坐标是（1，1），（4，5）
则曼哈顿距离是7，欧式距离是5

三、K-means中的k值如何选取

以下博文转自：https://blog.csdn.net/qq_15738501/article/details/79036255
通常我们会采用手肘法来确定k的值

1、手肘法

1.1理论

手肘法的核心指标是SSE(sum of the squared errors，误差平方和)，

其中，Ci是第i个簇，p是Ci中的样本点，mi是Ci的质心（Ci中所有样本的均值），SSE是所有样本的聚类误差，代表了聚类效果的好坏。

     手肘法的核心思想是：随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，
   那么误差平方和SSE自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个
   簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回
   报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE
   和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。当然，这也是该
   方法被称为手肘法的原因。

1.2 实践

我们对预处理后数据.csv 中的数据利用手肘法选取最佳聚类数k。具体做法是让k从1开始取值直到取到你认为合适的上限(一般来说这个上限不会太大，这里我们选取上限为8)，对每一个k值进行聚类并且记下对于的SSE，然后画出k和SSE的关系图（毫无疑问是手肘形），最后选取肘部对应的k作为我们的最佳聚类数。python代码如下所示：

import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
 
df_features = pd.read_csv(r'C:\预处理后数据.csv',encoding='gbk') # 读入数据
'利用SSE选择k'
SSE = []  # 存放每次结果的误差平方和
for k in range(1,9):
    estimator = KMeans(n_clusters=k)  # 构造聚类器
    estimator.fit(df_features[['R','F','M']])
    SSE.append(estimator.inertia_)
X = range(1,9)
plt.xlabel('k')
plt.ylabel('SSE')
plt.plot(X,SSE,'o-')
plt.show()

k与SSE的关系图如下：

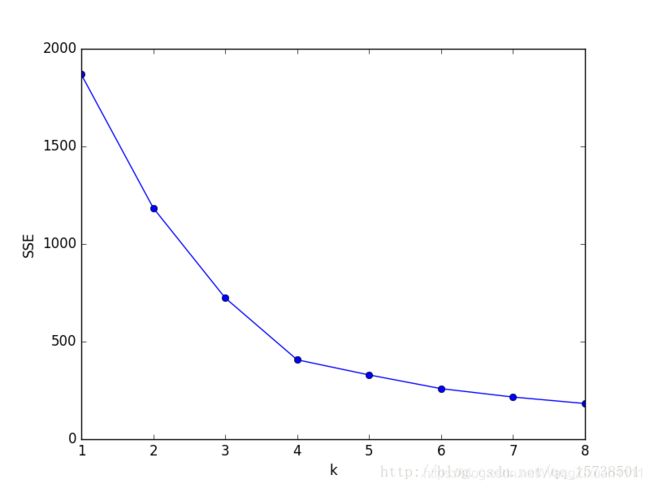
显然，肘部对于的k值为4，故对于这个数据集的聚类而言，最佳聚类数应该选4

2. 轮廓系数法

2.1 理论

该方法的核心指标是轮廓系数（Silhouette Coefficient），某个样本点Xi的轮廓系数定义
如下：

其中，a是Xi与同簇的其他样本的平均距离，称为凝聚度，b是Xi与最近簇中所有样本的平均距离，称为分离度。而最近簇的定义是

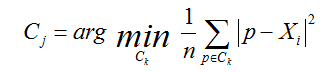
其中p是某个簇Ck中的样本。事实上，简单点讲，就是用Xi到某个簇所有样本平均距离作为衡量该点到该簇的距离后，选择离Xi最近的一个簇作为最近簇。

   求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范围为[-1,1]，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。那么，很自然地，平均轮廓系数最大的k便是最佳聚类数。

2.2 实践

我们同样使用2.1中的数据集，同样考虑k等于1到8的情况，对于每个k值进行聚类并且求出相应的轮廓系数，然后做出k和轮廓系数的关系图，选取轮廓系数取值最大的k作为我们最佳聚类系数
聚类数k与轮廓系数的关系图：

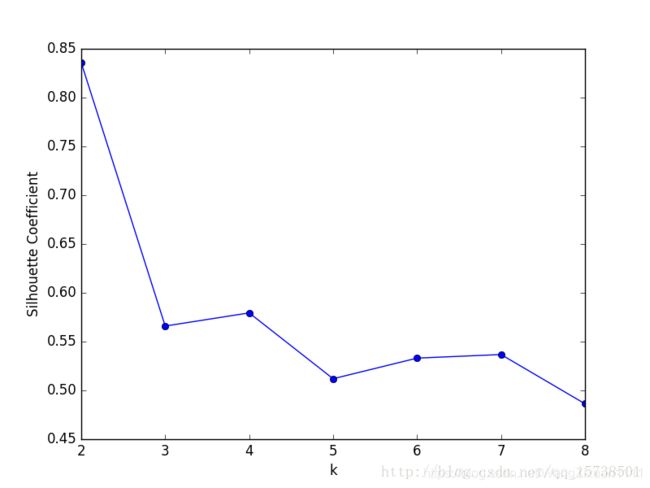
可以看到，轮廓系数最大的k值是2，这表示我们的最佳聚类数为2。但是，值得注意的是，从k和SSE的手肘图可以看出，当k取2时，SSE还非常大，所以这是一个不太合理的聚类数，我们退而求其次，考虑轮廓系数第二大的k值4，这时候SSE已经处于一个较低的水平，因此最佳聚类系数应该取4而不是2。

   但是，讲道理，k=2时轮廓系数最大，聚类效果应该非常好，那为什么SSE会这么大呢？在我看来，
   原因在于轮廓系数考虑了分离度b，也就是样本与最近簇中所有样本的平均距离。为什么这么说，
   因为从定义上看，轮廓系数大，不一定是凝聚度a（样本与同簇的其他样本的平均距离）小，而可
   能是b和a都很大的情况下b相对a大得多，这么一来，a是有可能取得比较大的。a一大，样本与同
   簇的其他样本的平均距离就大，簇的紧凑程度就弱，那么簇内样本离质心的距离也大，从而导致
   SSE较大。所以，虽然轮廓系数引入了分离度b而限制了聚类划分的程度，但是同样会引来最优结
   果的SSE比较大的问题，这一点也是值得注意的。

四、其他问题的解答

4、K-means算法中初始点的选择对最终结果有影响吗？

会有影响的，不同的初始值结果可能不一样

5、K-means聚类中每个类别中心的初始点如何选择？

（1）这k个点的距离尽可能远
（2）可以对数据先进行层次聚类（博客后期会更新这类聚类算法），得到K个簇之后，从每个类簇中选择一个点，该点可以是该类簇的中心点，或者是距离类簇中心点最近的那个点。

6、K-means中空聚类的处理

（1）选择一个距离当前任何质心最远的点。这将消除当前对总平方误差影响最大的点。
（2）从具有最大SSE的簇中选择一个替补的质心，这将分裂簇并降低聚类的总SSE。如果有多个空簇，则该过程重复多次。
（3）如果噪点或者孤立点过多，考虑更换算法，如密度聚类（博客后期会更新这类聚类算法）

7、K-means是否会一直陷入选择质心的循环停不下来？

（1）迭代次数设置
（2）设定收敛判断距离

8、如何快速收敛数据量超大的K-means？

相关解释可以去这个博客稍做了解https://blog.csdn.net/sunnyxidian/article/details/89630815

9、K-means算法的优点和缺点是什么？

K-Means的主要优点：
（1）原理简单，容易实现
（2）可解释度较强

K-Means的主要缺点：
（1）K值很难确定
（2）局部最优
（3）对噪音和异常点敏感
（4）需样本存在均值（限定数据种类）
（5）聚类效果依赖于聚类中心的初始化
（6）对于非凸数据集或类别规模差异太大的数据效果不好