数字电路设计之Wallace树形乘法器
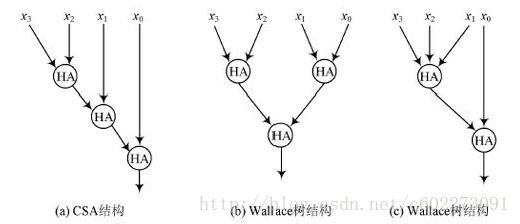
这个乘法器是先使用乘法表达试的相乘形式,然后把每一项表示出来。然后每一列就可以用全加器实现,分成多层来做,因为每个全加器只能有a,b,cin三个一位的输入。然后接着层层算,最后算到只有一位大小的时候就直接相加。Wallace在1964年提出采用树形结构减少多个数累加次数的方法,成为wallace树结构加法器。wallance树充分利用全加器3-2压缩的特性,随时将可利用的所有输入和中间结果及时并行计算,大大节省了计算延时。下图是wallance树型结构和CSA结构的对比。其结构的关键特性在于利用不规则的树形结构对所有的准备好输入数据的运算及时并行处理。
代码:
module signed_multi(a,b,result);//in this module,you can find that you can initial the value of wire
input [7:0] a,b;
output [15:0] result;
wire [7:0] a,b;
wire [15:0] result;
reg [7:0] p[7:0];
integer i,j;
always @(*) begin
for(i = 0;i <= 7;i = i + 1)
for(j = 0;j <= 7;j = j + 1)
p[i][j] = a[i]&b[j];
end
assign result[0] = p[0][0];
//--------------------level 1----------------------
wire [2:0] s1[12:1];
wire [2:0] c1[13:2]; //index can be a to non-zero
//index 14: p[7][7]
//index 13: p[7][6],p[6][7]
parameter zero = 1'b0;
assign result[1] = s1[1][0];
add fa1_01_0(p[1][0],p[0][1],zero,s1[1][0],c1[2][0]); //s[1] is result[1]
add fa1_02_0(p[2][0],p[0][2],p[1][1],s1[2][0],c1[3][0]);
add fa1_03_0(p[3][0],p[2][1],p[1][2],s1[3][0],c1[4][0]); //p[0][3]
add fa1_04_0(p[4][0],p[3][1],p[2][2],s1[4][0],c1[5][0]);
add fa1_04_1(p[1][3],p[0][4],zero, s1[4][1],c1[5][1]);
add fa1_05_0(p[5][0],p[4][1],p[3][2],s1[5][0],c1[6][0]);
add fa1_05_1(p[2][3],p[1][4],p[0][5],s1[5][1],c1[6][1]);
add fa1_06_0(p[6][0],p[5][1],p[4][2],s1[6][0],c1[7][0]);
add fa1_06_1(p[3][3],p[2][4],p[1][5],s1[6][1],c1[7][1]); //p[0][6]
add fa1_07_0(p[7][0],p[6][1],p[5][2],s1[7][0],c1[8][0]);
add fa1_07_1(p[4][3],p[3][4],p[2][5],s1[7][1],c1[8][1]);
add fa1_07_2(p[1][6],p[0][7],zero, s1[7][2],c1[8][2]);
add fa1_08_0(p[7][1],p[6][2],p[5][3],s1[8][0],c1[9][0]);
add fa1_08_1(p[4][4],p[3][5],p[2][6],s1[8][1],c1[9][1]); //p[1][7]
add fa1_09_0(p[7][2],p[6][3],p[5][4],s1[9][0],c1[10][0]);
add fa1_09_1(p[4][5],p[3][6],p[2][7],s1[9][1],c1[10][1]);
add fa1_10_0(p[7][3],p[6][4],p[5][5],s1[10][0],c1[11][0]);
add fa1_10_1(p[4][6],p[3][7],zero, s1[10][1],c1[11][1]);
add fa1_11_0(p[7][4],p[6][5],p[5][6],s1[11][0],c1[12][0]);//p[4][7]
add fa1_12_0(p[7][5],p[6][6],p[5][7],s1[12][0],c1[13][0]);
//--------------------level 2----------------------
wire [1:0] s2[13:2];
wire [1:0] c2[14:3];
assign result[2] = s2[2][0];
add fa2_02_0(s1[2][0],c1[2][0],zero, s2[2][0],c2[3][0]);
add fa2_03_0(s1[3][0],p[0][3], c1[3][0],s2[3][0],c2[4][0]);
add fa2_04_0(s1[4][0],s1[4][1],c1[4][0],s2[4][0],c2[5][0]); //c1[5][1]
add fa2_05_0(s1[5][0],s1[5][1],c1[5][0],s2[5][0],c2[6][0]);
add fa2_06_0(s1[6][0],s1[6][1],p[0][6], s2[6][0],c2[7][0]);
add fa2_06_1(c1[6][0],c1[6][1],zero, s2[6][1],c2[7][1]);
add fa2_07_0(s1[7][0],s1[7][1],s1[7][2],s2[7][0],c2[8][0]);
add fa2_07_1(c1[7][0],c1[7][1],zero, s2[7][1],c2[8][1]);
add fa2_08_0(s1[8][0],s1[8][1],p[1][7], s2[8][0],c2[9][0]);
add fa2_08_1(c1[8][0],c1[8][1],c1[8][2],s2[8][1],c2[9][1]);
add fa2_09_0(s1[9][0],s1[9][1],c1[9][0],s2[9][0],c2[10][0]);//c1[9][1]
add fa2_10_0(s1[10][0],s1[10][1],c1[10][0],s2[10][0],c2[11][0]);//c1[10][1]
add fa2_11_0(s1[11][0],p[4][7],c1[11][0], s2[11][0],c2[12][0]);//c1[11][1]
add fa2_12_0(s1[12][0],c1[12][0],zero, s2[12][0],c2[13][0]);
add fa2_13_0(c1[13][0],p[6][7],p[7][6], s2[13][0],c2[14][0]);
//--------------------level 3----------------------
wire [11:3] s3;
wire [12:4] c3;
assign result[3] = s3[3];
add fa3_03_0(zero,c2[3][0],s2[3][0],s3[3],c3[4]);
add fa3_04_0(zero,c2[4][0],s2[4][0],s3[4],c3[5]);
add fa3_05_0(s2[5][0],c1[5][1],c2[5][0],s3[5],c3[6]);
add fa3_06_0(s2[6][0],s2[6][1],c2[6][0],s3[6],c3[7]);
add fa3_07_0(s2[7][0],s2[7][1],c2[7][0],s3[7],c3[8]);//c2[7][1]
add fa3_08_0(s2[8][0],s2[8][1],c2[8][0],s3[8],c3[9]);//c2[8][1]
add fa3_09_0(s2[9][0],c1[9][1],c2[9][0],s3[9],c3[10]);//c2[9][1]
add fa3_10_0(s2[10][0],c1[10][1],c2[10][0],s3[10],c3[11]);
add fa3_11_0(s2[11][0],c1[11][1],c2[11][0],s3[11],c3[12]);
//--------------------level 4----------------------
wire [14:4] s4;
wire [15:5] c4;
assign result[4] = s4[4];
add fa4_04_0(zero,s3[4],c3[4],s4[4],c4[5]);
add fa4_05_0(zero,s3[5],c3[5],s4[5],c4[6]);
add fa4_06_0(zero,s3[6],c3[6],s4[6],c4[7]);
add fa4_07_0(c2[7][1],s3[7],c3[7],s4[7],c4[8]);
add fa4_08_0(c2[8][1],s3[8],c3[8],s4[8],c4[9]);
add fa4_09_0(c2[9][1],s3[9],c3[9],s4[9],c4[10]);
add fa4_10_0(zero,s3[10],c3[10],s4[10],c4[11]);
add fa4_11_0(zero,s3[11],c3[11],s4[11],c4[12]);
add fa4_12_0(c2[12][0],s2[12][0],c3[12],s4[12],c4[13]);
add fa4_13_0(zero,s2[13][0],c2[13][0],s4[13],c4[14]);
add fa4_14_0(p[7][7],c2[14][0],zero,s4[14],c4[15]);
assign result[15:5] = {zero,s4[14:5]} + c4[15:5];
endmodulemodule add(a,b,cin,s,cout);
input wire a,b,cin;
output wire s,cout;
assign {cout,s} = a + b + cin;
endmodule综合结果:
Tip:
以上的乘法器是无符号的,如果要是想计算有符号的乘法。那么就可以在原来的基础上加上16‘1000_0001_0000_0000(第一个1好加,只要最后加上即可。中间那个1就会使得第一级那里多一个加法器,整个的结构有点改变。)另外需要将一些p值取反,a或者b的index有7的就要再将a&b之后取反。