Context-aware Sequential Recommendation 论文&代码阅读
Liu Q , Wu S , Wang D , et al. Context-aware Sequential Recommendation[J]. 2016 IEEE 16th International Conference on Data Mining.
论文链接: https://arxiv.org/pdf/1609.05787.pdf.
Introduction
这篇文章是最早的将context上下文情景信息结合入Sequential Recommendation的文章,论文作者主要将一些购物时的时间信息理解为context进行处理,提取出了两种context:input context主要由购物日期在一周中的哪一天,以及一月中的哪一旬等组成;transition context这里用的是序列中相邻行为的时间间隔。
原理分析
先看一下论文给出的算法原理:

每一层hidden layer的计算方式由下式给出:
h k u = f ( r k u M c I , k u + h k − 1 u W [ t k μ − t k − 1 μ ] ] ) \left.\boldsymbol{h}_{k}^{u}=f\left(\boldsymbol{r}_{\boldsymbol{k}}^{u} \boldsymbol{M}_{c_{I, k}^{u}}+\boldsymbol{h}_{k-1}^{u} \boldsymbol{W}_{\left[t_{k}^{\mu}-\boldsymbol{t}_{k-1}^{\mu}\right]}\right]\right) hku=f(rkuMcI,ku+hk−1uW[tkμ−tk−1μ]])
其中 h k u \boldsymbol{h}_{\boldsymbol{k}}^{\boldsymbol{u}} hku是用户 u 的行为序列在时刻的 d 维 hidden status, r k u \boldsymbol{r}_{\boldsymbol{k}}^{\boldsymbol{u}} rku表示对应物品 v k u \boldsymbol{v}_{\boldsymbol{k}}^{\boldsymbol{u}} vku的 d 维 latent vector,激活函数 f(x) 使用 sigmoid 函数; M c I , k u \boldsymbol{M}_{\boldsymbol{c}_{I, \boldsymbol{k}}^{u}} McI,ku表示输入上下文 c I , k u c_{I, k}^{u} cI,ku特定的 dd 维输入矩阵, W [ t k − t k − 1 ] W_{\left[t_{k}-t_{k-1}\right]} W[tk−tk−1]是转移上下文 c T , k u c_{T, k}^{u} cT,ku特定的 dd 维自适应转移矩阵,在论文中直接由相邻时间戳的时间间隔得到(此处做了离散的时间划分)。
上面通过 RNN 的隐藏状态对历史行为上下文进行了建模。同时考虑到当前的上下文 c T , k + 1 u c_{T, k+1}^{\mathrm{u}} cT,k+1u, c I , k + 1 u c_{I, k+1}^{\mathrm{u}} cI,k+1u也会对推荐行为产生影响,因此最终的预测函数:
y u , k + 1 , v = h k u W c f , k + 1 ′ ( r v M c k + 1 ′ ) T y_{u, k+1, v}=\mathbf{h}_{\mathbf{k}}^{\mathbf{u}} \mathbf{W}_{\mathbf{c}_{\mathbf{f}, \mathbf{k}+1}}^{\prime}\left(\mathbf{r}_{\mathbf{v}} \mathbf{M}_{\mathbf{c}_{\mathbf{k}+1}}^{\prime}\right)^{T} yu,k+1,v=hkuWcf,k+1′(rvMck+1′)T
参数学习主要使用了 BPR(贝叶斯个性化排序)和 BPTT(时序反向传播)。BPR的基本假设是用户总是偏向于选择的物品而非负样本,因此在序列中的第 k 步需要实现如下概率的最大化:
p ( u , k , v > v ′ ) = g ( y u , k , v − y u , k , v ′ ) p\left(u, k, v>v^{\prime}\right)=g\left(y_{u, k, v}-y_{u, k, v^{\prime}}\right) p(u,k,v>v′)=g(yu,k,v−yu,k,v′)
结合负对数似然比之后可以得到CA-RNN的目标函数
J = ∑ u , k ln ( 1 + e − ( y u , k , v − y u , k , v ′ ) ) + λ 2 ∣ θ ∣ 2 J=\sum_{u, k} \ln \left(1+e^{-\left(y_{u, k, v}-y_{u, k, v^{\prime}}\right)}\right)+\frac{\lambda}{2}|\theta|^{2} J=u,k∑ln(1+e−(yu,k,v−yu,k,v′))+2λ∣θ∣2
其中Θ={R,M,W}表示所有需要学习的参数,λ为正则化超参数。
看论文的时候实在没看懂 context matrix 的计算方式,而且源码用的是python 2版本,不想调试了,就大概看了一下,把代码的实现过程也贴在下面。后面再补一些BPR和BPTT的具体原理。
代码阅读
论文里给出的CARNNcode.zip里面包含三种实现方法:CARNN,CARNN_Input和RNN+BPR;以及三个数据集user_cart_input+transition.json,user_cart_input.json和user_cart_basic.json。这次主要看CARNN.py。
// CARNN.py
USER_SIZE = 1904 # 总用户数
ITEM_SIZE = 1157 # 总商品种数
HIDDEN_SIZE = 40 # hidden layer的维度
LEARNING_RATE = 0.01 # 学习速率
LAMBDA = 0.001 # 惩罚系数
TOP = 20 # recall取前Top个
H_ZERO = np.zeros((1, HIDDEN_SIZE)) #零初始化hidden layer,size=(1,40)
X = np.random.randn(ITEM_SIZE, HIDDEN_SIZE)*0.5
W = np.random.randn(HIDDEN_SIZE, HIDDEN_SIZE)*0.5 #随机初始化输入矩阵 X 和权重矩阵 W
UWF = [] # 第一个weekday转移矩阵
UWS = [] # 第二个weekday转移矩阵
UMF = [] # 第一个month转移矩阵
UMS = [] # 第二个month转移矩阵
VF = [] # 第一个interval转移矩阵
VS = [] # 第二个interval转移矩阵(这里是作者的注释,个人感觉用historial / current context transition matrix命名更加合适)
for i in range (7):
uw = np.random.randn(HIDDEN_SIZE, HIDDEN_SIZE)*0.5
UWF.append(uw)
UWS.append(uw)
for i in range (3):
um = np.random.randn(HIDDEN_SIZE, HIDDEN_SIZE)*0.5
UMF.append(um)
UMS.append(um)
for i in range(5):
v = np.random.randn(HIDDEN_SIZE, HIDDEN_SIZE)*0.5
VF.append(v)
VS.append(v) # 随机初始化六个状态转移矩阵,记录每个context的转移矩阵
RECALL_MAX = {}
ITER_MAX = 0
for i in range(TOP):
RECALL_MAX[i+1] = 0 # 取前20的最优recall指标
DATAFILE = 'user_cart_input+transition.json' # 路径文件名
ITEM_TRAIN = {}
ITEM_TEST = {}
WEEKDAY_TRAIN = {}
WEEKDAY_TEST = {}
MONTH_TRAIN = {}
MONTH_TEST = {}
INTERVAL_TRAIN = {}
INTERVAL_TEST = {} # 待读取的数据集
SPLIT = 0.9
def train(user_cart, weekday_cart, month_cart, interval_cart):
# 后面主函数里会看到,这里的user_cart等参数就是ITEM_TRAIN[i]……等单个用户的行为转移序列
global U, W, X
dhlist = [] # BPR中对h的导数
hiddenlist = [] # 记录[1,T]状态hidden layer (不包括1的上一个状态的hidden layer)
midlist = [] # BPTT中传到第一层的导数 sigmoid(bi)*(1-sigmoid(bi))
hl = np.copy(H_ZERO) # 初始化last hidden layer
sumdUW = []
sumdUM = []
sumdV = [] # 记录对于每一个用户BPTT中u、w、m、v总更新量
loss = 0
for i in range(7):
sumdUW.append(0)
for i in range(3):
sumdUM.append(0)
for i in range(5):
sumdV.append(0)
# BPR
dh1 = np.copy(H_ZERO) # dh for the back process
for i in xrange(len(user_cart)-1): # i stands for a time step in sequence
neg = random.randint(1, ITEM_SIZE)
while (user_cart[i+1]) == neg: # 这里的user_cart[i+1] 是序列里下一个 item
neg = random.randint(1, ITEM_SIZE) # 对于要预测的item进行负采样
item_pos = X[user_cart[i+1]-1, :].reshape(1, HIDDEN_SIZE) # X = np.random.randn(ITEM_SIZE, HIDDEN_SIZE)*0.5
item_curt = X[user_cart[i]-1, :].reshape(1, HIDDEN_SIZE) # 所以reshape有啥用呢,疑惑中
item_neg = X[neg-1, :].reshape(1, HIDDEN_SIZE) # 分别是positive、current input 和 negative sample's vector
month_now = month_cart[i]
month_next = month_cart[i+1]
weekday_now = weekday_cart[i]
weekday_next = weekday_cart[i+1]
interval_now = interval_cart[i]
interval_next = interval_cart[i+1]
uw_now = UWF[weekday_now]
uw_next = UWS[weekday_next]
um_now = UMF[month_now]
um_next = UMS[month_next]
v_now = VF[interval_now]
v_next = VS[interval_next] # 这样就是在每一个转移矩阵里,分别取到当前时刻和下一时刻的context
b = np.dot(item_curt, (uw_now + um_now)) + np.dot(hl, v_now)
h = sigmoid(b) # 这里对应公式一,计算某一用户当前时刻的 hidden status
xi_j = item_pos - item_neg
xij = np.dot(np.dot(h, (uw_next + um_next + v_next)), xi_j.T) # xij对应公式三的正负预测值之差
loss += xij
tmp = -(1 - sigmoid(xij)) # 这里tmp代表的是公式四损失函数的导数,∂J/∂xij
# "若为tmp = sigmoid(-Xij) 则LEARNING_RATE和LAMBDA为负" 没懂这句在讲啥
hiddenlist.append(h)
mid = h * (1 - h)
midlist.append(mid) # midlist储存的是每一层hidden layer h 对于 b 的导数,dhlist储存的是BPR每一步对于 h 的导数
dhlist.append(tmp * np.dot(item_pos - item_neg, (uw_next.T + um_next.T + v_next.T))) # save the dh for each BPR step
dneg = -tmp * np.dot(h, (uw_next + um_next + v_next)) + LAMBDA * item_neg # 这里tmp乘的东西是 ∂xij/∂h,所以负样本就要乘上负号吗
X[neg-1, :] += -LEARNING_RATE * (dneg.reshape(HIDDEN_SIZE, ))
ditem = tmp * np.dot(h, (uw_next + um_next + v_next)) + LAMBDA * item_pos
X[user_cart[i+1]-1, :] += -LEARNING_RATE * (ditem.reshape(HIDDEN_SIZE,)) # 计算对于正、负样本的导数 并更新正样本的vector
dUWS = tmp * np.dot(h.T, (item_pos - item_neg)) # 计算next UW的更新量 dUW = tmp * np.dot((item_pos - item_neg).T, h)
UWS[weekday_next] += -LEARNING_RATE * (dUWS + LAMBDA * UWS[weekday_next])
dUMS = tmp * np.dot(h.T, (item_pos - item_neg))
UMS[month_next] += -LEARNING_RATE * (dUMS + LAMBDA * UMS[month_next])
dVS = tmp * np.dot(h.T, (item_pos - item_neg))
VS[interval_next] += -LEARNING_RATE * (dVS + LAMBDA * VS[interval_next]) # UW、UM、V 分别单独求导迭代
hl = h # 更新last hidden layer
# BPTT
for i in range(len(user_cart) - 1)[::-1]:
item = X[user_cart[i] - 1, :].reshape(1, HIDDEN_SIZE)
month_now = month_cart[i]
weekday_now = weekday_cart[i]
interval_now = interval_cart[i]
uw_now = UWF[weekday_now]
um_now = UMF[month_now]
v_now = VF[interval_now]
hnminus2 = hiddenlist[i]
dh = dhlist[i] + dh1
dUW = np.dot(item.T, dh * midlist[i])
dUM = np.dot(item.T, dh * midlist[i])
dV = np.dot(hnminus2.T, dh * midlist[i]) # 计算 ∂J/∂W(M、V),所以在算出 ∂J/∂b 后还要乘以各自的系数 ∂b/∂θ
sumdUW[weekday_now] += dUW
sumdUM[month_now] += dUM
sumdV[interval_now] += dV
dx = np.dot(dh * midlist[i], (uw_now.T + um_now.T)) # 计算 ∂J/∂x,更新输入的样本
X[user_cart[i]-1, :] += -LEARNING_RATE*(dx.reshape(HIDDEN_SIZE, ) + LAMBDA * X[user_cart[i]-1, :])
dh1 = np.dot(dh * midlist[i], v_now.T)
for month in range(3): # 到这里终于把训练的转移矩阵更新了一次!虽然没有实际做,但是看完了还是很开心……
UMF[month] += -LEARNING_RATE * (sumdUM[month] + LAMBDA * UMF[month])
for weekday in range(7):
UWF[weekday] += -LEARNING_RATE * (sumdUW[weekday] + LAMBDA * UWF[weekday])
for interval in range(5):
VF[interval] += -LEARNING_RATE *(sumdV[interval] + LAMBDA * VF[interval])
return loss
def predict():
relevant = 0.0 # 所预测的总次数
hit = {} # 第n个位置所命中的个数
recall = {} # 前n个位置所命中的总数
recallatx = {} # Recall At N/relevant
for i in range(TOP): # recall取前Top=20个
hit[i+1] = 0
recall[i+1] = 0
for n in ITEM_TEST.keys(): # n代表一个用户
item_train = ITEM_TRAIN[n]
item_test = ITEM_TEST[n]
month_train = MONTH_TRAIN[n]
month_test = MONTH_TEST[n]
weekday_train = WEEKDAY_TRAIN[n]
weekday_test = WEEKDAY_TEST[n]
interval_train = INTERVAL_TRAIN[n]
interval_test = INTERVAL_TEST[n]
hl = np.copy(H_ZERO)
h = np.copy(H_ZERO)
for i in range(len(item_train)): # i 表示单个用户行为序列里的一个time step
month_now = month_train[i]
weekday_now = weekday_train[i]
interval_now = interval_train[i]
umf = UMF[month_now]
uwf = UWF[weekday_now]
vf = VF[interval_now]
item = X[item_train[i]-1]
b = np.dot(item, (uwf + umf)) + np.dot(hl, vf)
h = sigmoid(b)
hl = h # 计算需要预测的状态对应的hidden layer
for j in xrange(len(item_test)): # 预测
month_now = month_test[j]
weekday_now = weekday_test[j]
interval_now = interval_test[j]
ums = UMS[month_now]
uws = UWS[weekday_now]
vs = VS[interval_now]
relevant += 1
predict_matrix = np.dot(np.dot(h, (vs+uws+ums)), X.T)
rank = np.argpartition(predict_matrix[0], -TOP)[-TOP:]
rank = rank[np.argsort(predict_matrix[0][rank])] # np.argpartition和np.argsort这两个函数,常用于各种任务的top正确率计算
rank_index_list = list(reversed(list(rank))) # 输出预测矩阵的前 top=20 个结果的索引
if item_test[j]-1 in rank_index_list: # 输出预测矩阵是每个 user、每个 item 的预测得分,所以这里索引就是item的序号
index = rank_index_list.index(item_test[j]-1) # 查到top20里对应真实值的预测索引,就在对应位置的hit + 1
hit[index+1] += 1
item = X[item_test[j] - 1]
uwf = UWF[weekday_now]
umf = UMF[month_now]
vf = VF[interval_now]
b = np.dot(item, (uwf+umf)) + np.dot(h, vf) # 把 h 传到下一层继续预测
h = sigmoid(b)
for i in range(20):
for j in range(20-i):
recall[20-j] += hit[i+1] # 只要在第i个位置命中了,recall@1~recall@20都加1
for i in range(20):
recallatx[i+1] = recall[i+1]/relevant # 除以测试样本数
print relevant
print recall
print recallatx
return recall, recallatx
def save_max(result, n, iter):
global RECALL_MAX, ITER_MAX # 保存result[n]最大的result
if(result[n] > RECALL_MAX[n]): # 所以第10个最大 就认为结果最好了?(说好的记录Recall@20呢,取平均值的意思吗)
RECALL_MAX = result
ITER_MAX = iter
print "Best Result At Iter %i" %ITER_MAX
print RECALL_MAX
总结完之后,看一下复现的实验结果:

这里第一行是sumloss,第二行是测试的总物品数,后面两行分别是recall的物品数和比例。和论文结果比较一下:
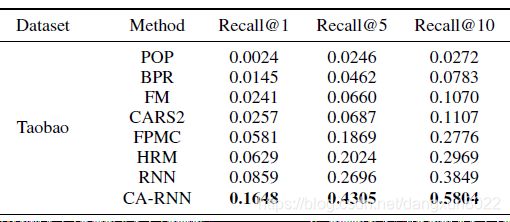
看起来结果还不错,Recall@1和Recall@5比原文结果稍低但是Recall@10还高了一些。