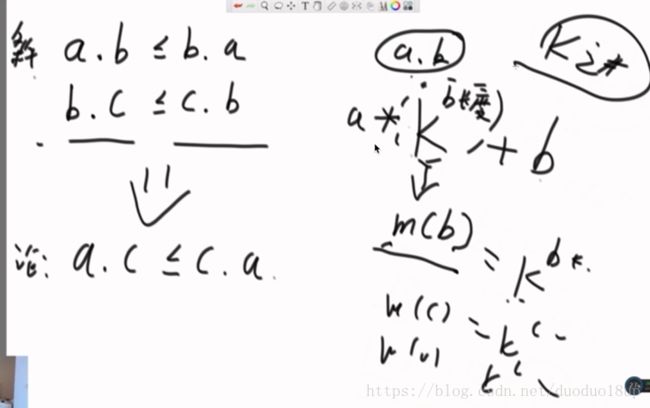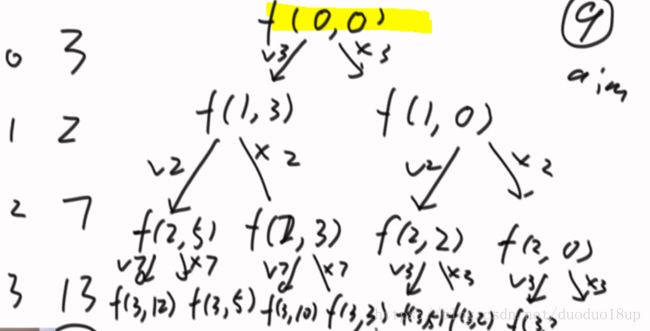左 . 算法--- 前缀树/贪心策略/递归/ 动态规划专题

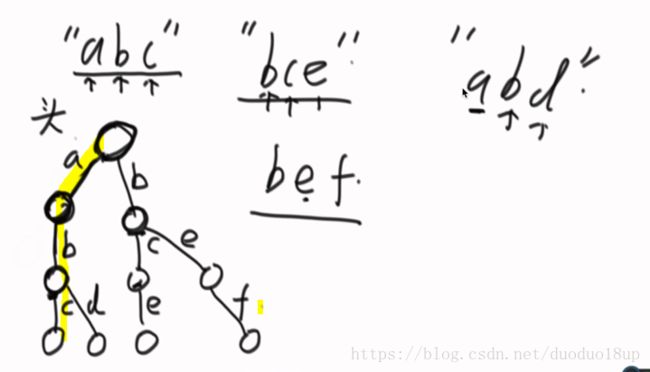
前缀树（TrieTree)：

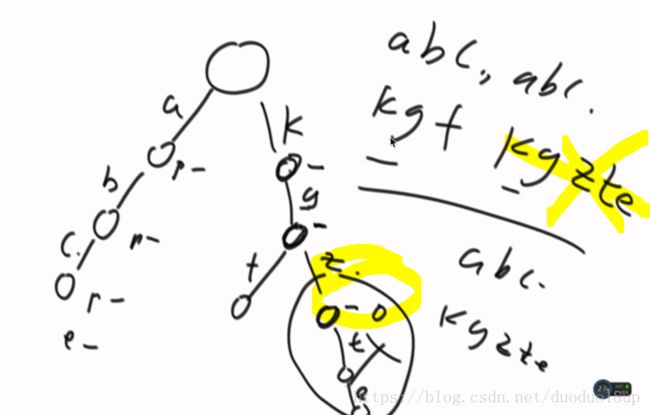
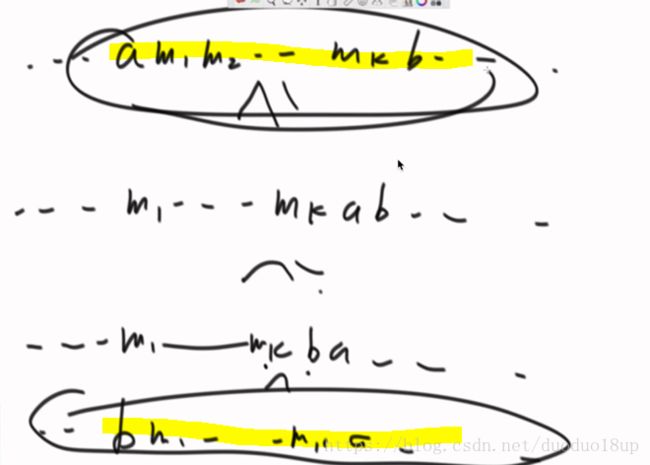
关于前缀树在实际中的用途以及 类型 见   前缀树的实际应用（面试可能会涉及到）----搜索方面的作用

举例：  如图所示   路径上标的是字符串中单个字符   

升级 1(查找是否有特定字符串）：

如果要查找"de"前缀的字符串，很好做到    但是查找是否有"de"字符串就不太好确定 （因为和"def"类似的结构是相同的）

所以   在刚才的基础上    在每个节点加上计数器 如果以此节点为末尾节点 则+1 

升级 2 ( 确定含有特定前缀的字符串个数 ）：

就在每个节点处开辟另一个参数区域 用来记录有几个字符串经过  经过一次 则区域计数+1

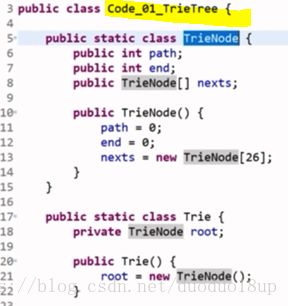
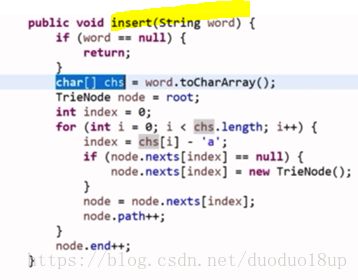
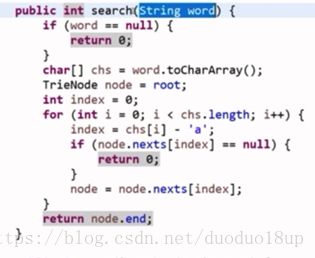
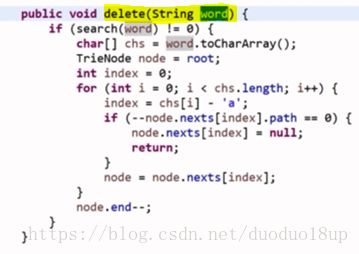
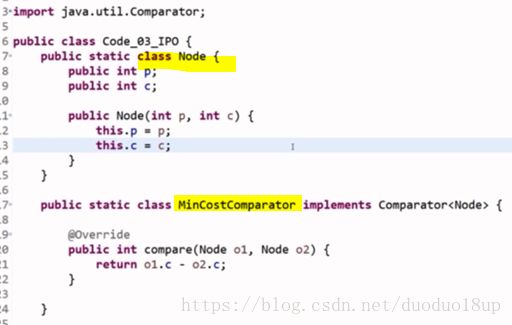
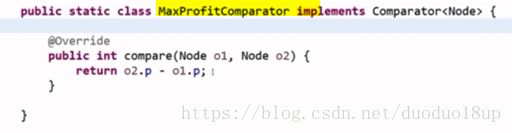
代码：

   

    

   

删除时候需要注意：如果某个节点已经为0  则其子节点也就不要了~~直接赋值为null

应用：

给定一个数组 求子数组的最大异或和

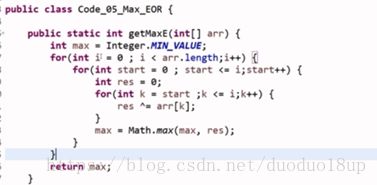
思路1 ：暴力解  时间复杂度太高！

  0---i   1--i   ....i--i   每一个O(n) *O(n)   一共有n个数  则o(N)  *o(n2)=o(n3)

思路2 ：利用0---i 的异或结果=o---start -1 （dp[start-1] ) ^ start---i

时间复杂度O(n2)

结论：

思路3：时间复杂度O(n)

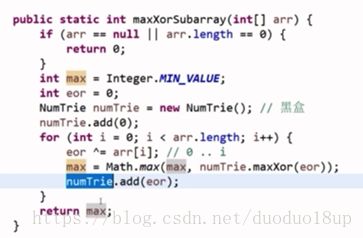
采用前缀树的思想去做这个题：

1   假设有个黑盒结构    我们记录EOR （0--i) 黑盒自动帮我们匹配…… EOR最大的数

2  其实这是利用前缀树帮我们实现的   我们知道一部分 另一部分我们去匹配时就可以找到最优了

例如  3 是1100  则以3为结尾的最大数组异或和  尽量为1011  第一位符号位尽量为0 （正） 其他尽量保留1

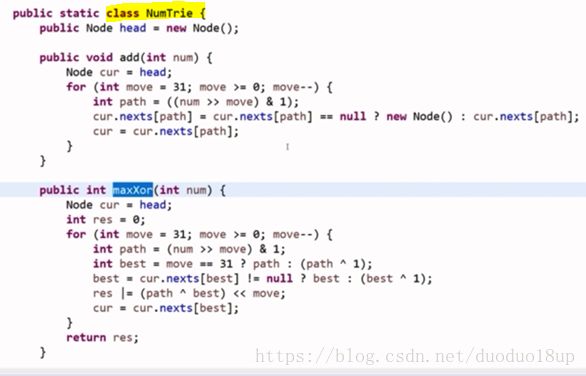
3  代码实现：

NumTrie视为黑盒

NumTrie

path : 每一位为0/1

move==31: 符号位

maxXor  :  0---i的异或结果

best :期待要选的路

下一best : 实际选择的路

res :设置答案的每一位

cur :继续往下走

贪心策略

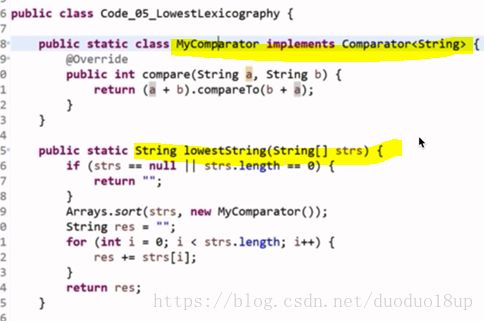
给定几个字符串，将它们拼接起来构成最小的字符串（字典序）：

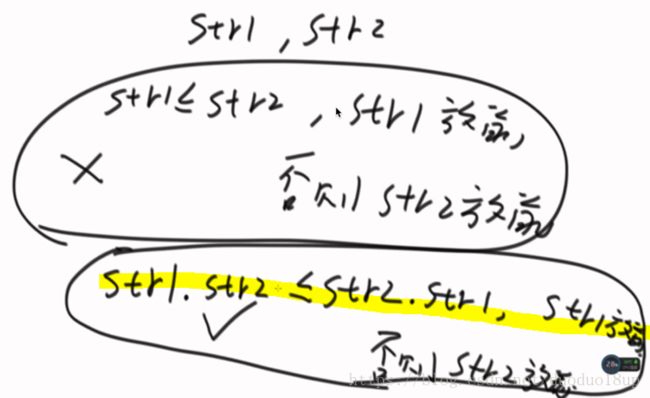
贪心策略1 ： 按照分部字典序去拼接----不一定整体是字典序最前的。

贪心策略2：  如果拼接起来是字典序最前的  -----则按照这个排下来。

分析贪心策略：必须具有传递性----这样上述条件才成立

如果是在数字类型题中 ，可以根据字符串最终还原成连接起来的数字形式。  

K进制    则  前面的a*k(b长度）+b----表示成整体连接之后的数字形式

证明可以得出：

再证明：

假设有a----b----     证明a放在前面一定是最好的选择  

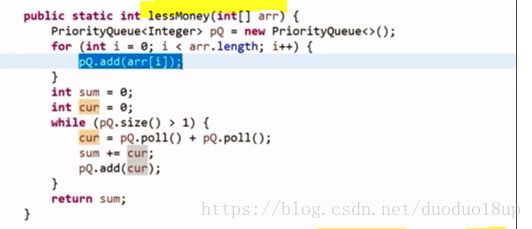
贪心--分金条使代价最低：

思路： 类似于 霍夫曼树   最终统计的是   非叶子节点的总和

解决工具：  采用小根堆   每次取出其中最小的两个 类似于组建哈夫曼树  不断向上  

                   直到堆中只剩下一个元素   最终统计所有的求和

主要核心：  在于我们想去寻找两个尽可能大小相当的  所以堆这个结构刚刚好

代码：

总结：

当总共的代价由子代价 累加或者累乘  时 ，可能还会有对应的公式 ，则可能用哈夫曼编码的思路做出来。

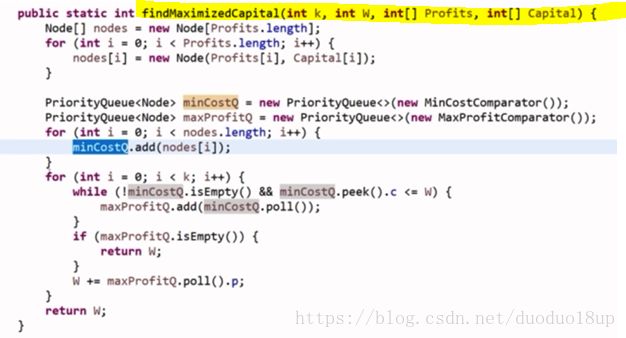
贪心--做有限项目使利润最大化：

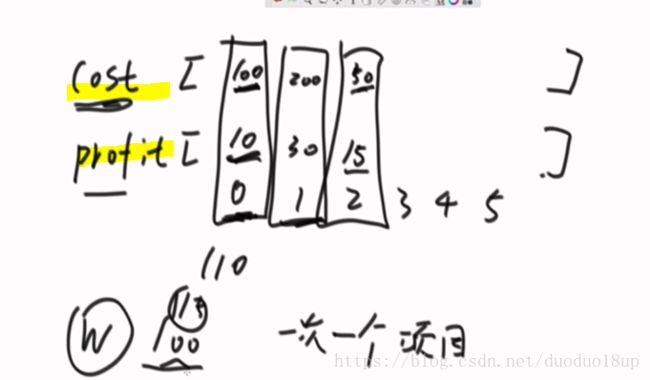
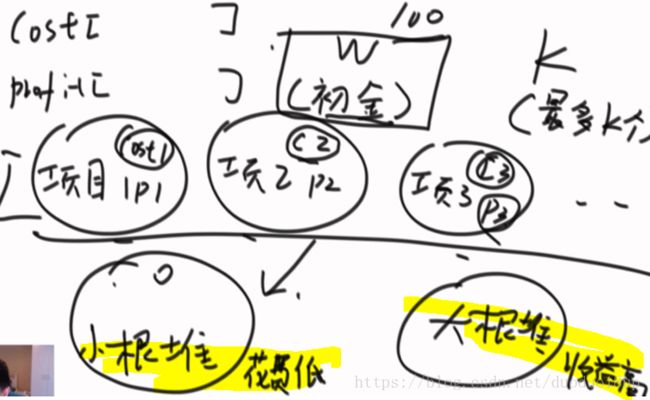
题意： 有一批项目 每个项目对应两个参数 一个cost（成本） 一个profit（利润）  

           最初给定一笔启动资金W   每次只能执行一个项目  （必须在资金以内的项目）    

           最多做K个项目   如何使最终获得的钱数最大~

思路：  小根堆---按照花费排（小根堆存放全部的项目）---取出未超过启动资金的花费项目

            ----再进入大根堆---按照利润排----（大根堆存放解锁的项目）

            不断的进行上述挑选--每次解锁一堆项目--从中拿出利润最大的进行---之后重复

         

代码：

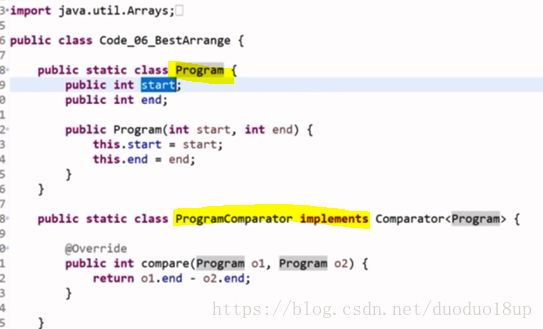
贪心--在有限时间内使会议室内宣讲场次最多：

思路：

考虑几种可能的贪心策略： 1  开始时间早（然而结束时间超级晚）

                                         2  持续时间短（然而 影响前后两个宣讲场次）

                                         3  结束时间短的~~（为最可能的）

代码：

递归和动态规划：

   

求阶乘n!  :

递归和非递归写法:

汉诺塔问题：

时间复杂度为  2(n)-1  n次方

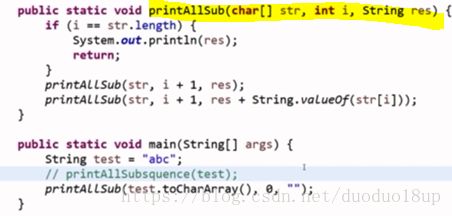
打印一个字符串的全部子序列，包括空字符串。

递归法：

原理：类似于二叉树  到叶子节点就开始打印

打印字符串的全排列：

母牛数量：

列举出前几项：

规律总结：

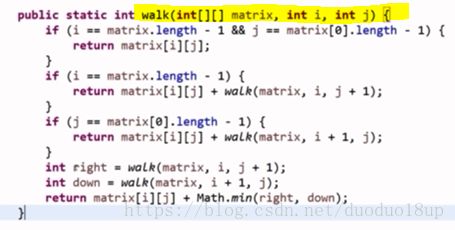
二维数组的最小路径和：

思路：

从(i,j)点出发到右下角点的最小路径和：

1  如果(i,j)就是 右下角点 则路径和  返回该点值 

2  如果已经到最后一行 则只能继续往右走  则该点值+右边点距离终点的最小路径和

3 如果已经到最后一列  则只能继续往下走  则该点值+ 下边点距离终点的最小路径和

4  如果是正常情况 可以向右 / 向下  则考察右端和下端具体最小路径和+ 该点值=最终最小路径和

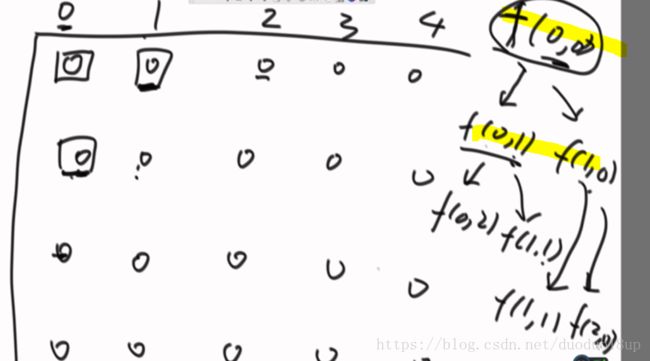
此种方法复杂度较高：

由图中可以看出  重复状态出现次数太多---暴力递归

暴力递归改动态规划：

其实变成了从下往上 递归  

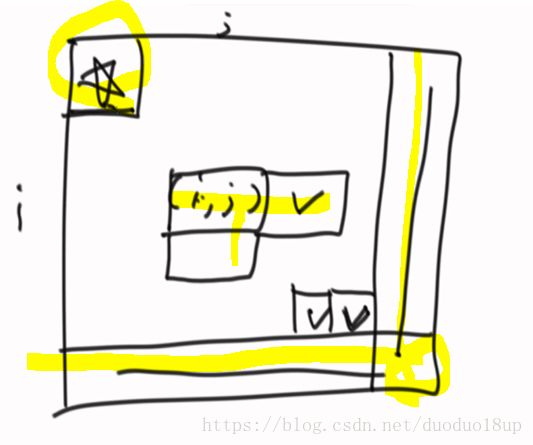
1  写出尝试版本（递归形式）

2 分析可变参数 分析哪几个参数可以代表返回值状态  可变参数几维 ---几维表

3 观察需要的终止状态--在表中点出--回到base  cases把完全不依赖的值设置好（如最后一行最后一列）

4  观察一个普遍位置 需要哪些位置  逆着回去 就是填表的顺序

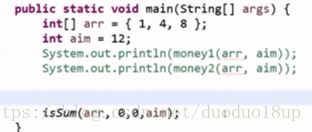
给定数组和特定数字，是否能够累加求和为该数字？

思路：

先想递归：

代码：

两种选择中有一个为true即整体为true

从暴力递归转成动态规划：

特殊情况考虑： 数组中全部数字总和都

考虑是否具有后效性  （与前面的选择无关)

考虑可变参数   数组固定数字固定 只有i和sum不固定

 画出dp图：最后一行是定的 由base case确定的

进阶篇 ------暴力递归改为动态规划

1 换钱的方法数：

1  暴力递归的试法：

假设数组 200 ,100,50,20,5,1   aim=1000

则 试法：  0 张200  后面解决1000

                 1张200  后面解决800 ....以此类推

2   加一个新参数index  代表index位置及其之后的数字可以进行选择

3 暴力递归  代码实现（不能通过code)：

时间复杂度为O(aim的N次方）   N为数组规模

4  暴力递归的缺点：  总有一些重复的计算不可避免

例如下图中 的600 其实是一样的  但是每次递归均要求解一遍  导致复杂度过高

5  发现：

分析上述问题 发现是无后效问题（ 如何到达状态我们不用管 只要是600 ）

   一旦index 和 aim固定下来 则之后的操作就是固定的

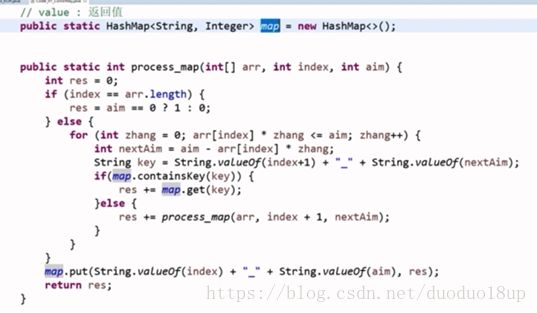
 所以利用一个map进行一个缓存 记录之前是否已经计算过某个值

6  代码实现(“记忆化搜索” 方法 ---通用）：

时间复杂度为O(N* aim2)   aim的平方

String :"index_aim"    value: 固定index和aim的返回值

之前是遍历时候直接进行调用 ---- 现在我们先获取key观察这种组合是否之前已经计算过

若之前已经计算过  则直接返回之前计算过的 值  否则就再次调用process进行结果计算

转 动态规划的思路：

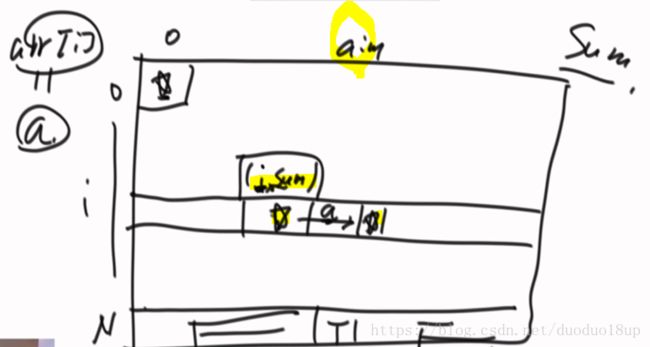
1  根据之前暴力递归的代码 分析得出二位表中哪些数据 是目前 已知的 以及要求解的

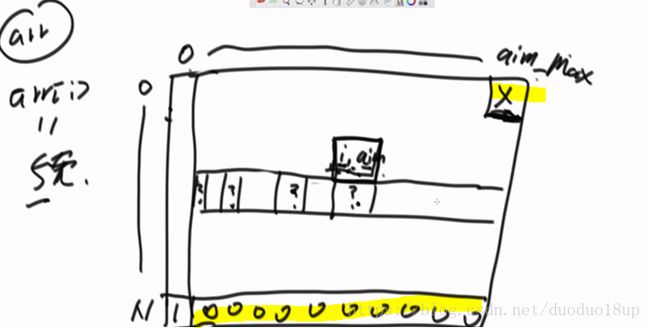
    观察我们主函数调用 求解 process( arr, 0, aim)    故在图上右上角位置的值为最终要求解的值

    观察 base case  则最后一行 数字为1  00  0000 00....

    观察最普遍的一个状态 (i ,aim)  由哪些值 决定  -----下面一行index+1  且个数为不超过 zhang ,

     aim- zhang* arr[index]=0

2  实例说明    图示如下：

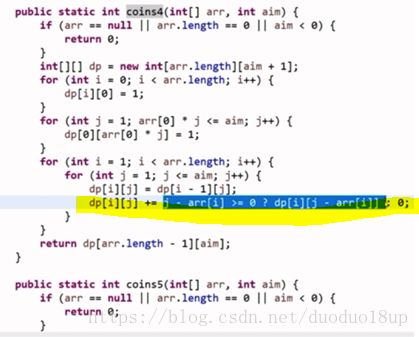
3    动态规划代码实现：

dp[i][j]的含义是： 在使用arr[0---i]货币的情况下 组成钱数j有多少种方法？

一般第一行和第一列容易是特殊情况~ 

本题中还有最后一行 也很特殊

分析时间复杂度：

4  总结：

记忆化搜索方法与动态规划方法本质上是一样的，故时间复杂度一样

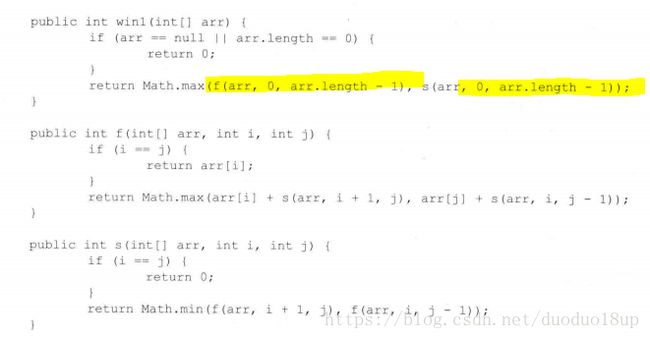
2   排成一条线的纸牌博弈问题：

思路分析：

1  暴力递归的方法：

代码实现：

2 动态规划的方法：

代码实现：