『数据结构』树

• 1. 概念
• 2. 二叉查找树
  
  • 2.1. 随机构造的二叉查找树
  • 2.2. 平均结点深度
  • 2.3. 不同的二叉树数目 (Catalan num)
  • 2.4. 好括号列
• 3. 基数树 (radixTree)
• 4. 字典树 (trie)
  
  • 4.1. AC 自动机
• 5. 平衡二叉树
  
  • 5.1. AVL Tree
  • 5.2. splayTree
    
    • 5.2.1. Zig-step
    • 5.2.2. Zig-zig step
    • 5.2.3. Zig-zag step
  • 5.3. read-black Tree
  • 5.4. treap
• 6. 总结
• 7. 附代码
  
  • 7.1. 二叉树 (binaryTree)
  • 7.2. 前缀树 (Trie)
  • 7.3. 赢者树 (winnerTree)
  • 7.4. 左斜堆

1. 概念

• 双亲
• 左右孩子
• 左右子树
• 森林
• 结点, 叶子, 边, 路径
• 高度 h
• 遍历 (前中后层)
• 结点数 n
  

2. 二叉查找树

又名排序二叉树, 对于每个结点, 如果有, 其左孩子不大于它, 右孩子不小于它

通过前序遍历或者后序遍历就可以得到有序序列 (升序, 降序)

常用三种操作, 插入, 删除, 查找, 时间复杂度是 O(h) O ( h )
h 是树高, 但是由于插入, 删除而导致树不平衡, 即可能 h⩾⌊logn⌋ h ⩾ ⌊ l o g n ⌋

2.1. 随机构造的二叉查找树

下面可以证明, 随机构造, 即输入序列有 n! n ! 中, 每种概率相同的情况下, 期望的树高 h=O(logn) h = O ( l o g n )

(直接搬运算法导论上面的啦>_<)

2.2. 平均结点深度

一个较 上面定理 弱的结论:

一棵随机构造的二叉查找树, n 个结点的平均深度为 O(logn) O ( l o g n )

类似 RANDOMIZED-QUICKSORT 的证明过程, 因为快排 递归的过程就是一个递归 二叉树.
随机选择枢纽元就相当于这里的某个子树的根结点 在所有结点的大小随机排名, 如 i. 然后根结点将剩下的结点划分为左子树 (i-1) 个结点, 右子树 (n-i) 个结点.

2.3. 不同的二叉树数目 (Catalan num)

给定 {1,2,…,n} { 1 , 2 , … , n } , 组成二叉查找树的数目.
由上面的证明过程, 可以容易地分析得出, 任选第 i 个数作为根, 由于二叉查找树的性质, 其左子树
应该有 i-1 个结点, 右子树有 n-i 个结点.
如果记 n 个结点 的二叉查找树的数目为 bn b n
则有递推公式

bn={1∑ni=1bi−1bn−in=0n⩾1 b n = { 1 n = 0 ∑ i = 1 n b i − 1 b n − i n ⩾ 1

然后我们来看 <<算法导论>>(p162, 思考题 12-4) 上怎么求的吧 (•̀ ω •́)y
设生成函数

B(x)=∑n=0∞bnxn B ( x ) = ∑ n = 0 ∞ b n x n

下面证明 B(x)=xB(x)2+1 B ( x ) = x B ( x ) 2 + 1
易得

xB(x)2=∑i=1∞∑n=i∞bi−1bn−ixn x B ( x ) 2 = ∑ i = 1 ∞ ∑ n = i ∞ b i − 1 b n − i x n

对比 B(x),xB(x)2+1 B ( x ) , x B ( x ) 2 + 1 的 x 的各次系数, 分别是 bk,ak b k , a k
当 k=0, ak=1=bk a k = 1 = b k
当 k>0

ak=∑i=1kbi−1bk−i=bk a k = ∑ i = 1 k b i − 1 b k − i = b k

所以 B(x)=xB(x)2+1 B ( x ) = x B ( x ) 2 + 1
由此解得

B(x)=1−1−4x−−−−−√2x B ( x ) = 1 − 1 − 4 x 2 x

在点 x=0 处,
用泰勒公式得

limx→01−4x−−−−−√=1+∑n=1∞C12n(−4)nxn=1+∑n=1∞(2n−3)!!(−4x)nn! lim x → 0 1 − 4 x = 1 + ∑ n = 1 ∞ C n 1 2 ( − 4 ) n x n = 1 + ∑ n = 1 ∞ ( 2 n − 3 ) ! ! ( − 4 x ) n n !

所以对应系数

bn=124n+1(2n−1)!!2n+1n!=Cn2nn+1 b n = 1 2 4 n + 1 ( 2 n − 1 ) ! ! 2 n + 1 n ! = C 2 n n n + 1

这个数叫做 Catalan 数

2.4. 好括号列

王树禾的<<图论>>(p42) 上用另外的方法给出 Catalan 数, 并求出 n 结点 二叉查找数的个数

首先定义好括号列, 有:
* 空列, 即没有括号叫做好括号列
* 若 A,B 都是好括号列, 则串联后 AB 是好括号列
* 若 A 是好括号列, 则 (A) 是好括号列

充要条件: 好括号列 ⟺ ⟺ 左右括号数相等, 且从左向右看, 看到的右括号数不超过左括号数

定理: 由 n 个左括号, n 个右括号组成的好括号列个数为 c(n)=Cn2nn+1 c ( n ) = C 2 n n n + 1

证明:
由 n 左 n 右组成的括号列有 2nn!n!=Cn2n 2 n n ! n ! = C 2 n n 个.
设括号列 a1a2…a2n a 1 a 2 … a 2 n 为坏括号列,
由充要条件, 存在最小的 j, 使得 a1a2…aj a 1 a 2 … a j 中右括号比左括号多一个,
由于是最小的 j, 所以 aj a j 为右括号, aj+1 a j + 1 为右括号
把 aj+1aj+2…a2n a j + 1 a j + 2 … a 2 n 中的左括号变为右括号, 右变左, 记为 a¯j+1a¯j+2…a¯2n a ¯ j + 1 a ¯ j + 2 … a ¯ 2 n

则括号列 a1a2…aja¯j+1 a 1 a 2 … a j a ¯ j + 1 为好括号列
a1a2…aja¯j+1a¯j+2…a¯2n a 1 a 2 … a j a ¯ j + 1 a ¯ j + 2 … a ¯ 2 n 可好可坏, 且有 n-1 个右, n+1 个左, 共有 2n(n+1)!(n−1)!=Cn+12n 2 n ( n + 1 ) ! ( n − 1 ) ! = C 2 n n + 1 个.

所以坏括号列 a1a2…a2n a 1 a 2 … a 2 n 与括号列 a1a2…aja¯j+1a¯j+2…a¯2n a 1 a 2 … a j a ¯ j + 1 a ¯ j + 2 … a ¯ 2 n , 有 2n(n+1)!(n−1)!=Cn+12n 2 n ( n + 1 ) ! ( n − 1 ) ! = C 2 n n + 1 个

那么好括号列有

c(n)=Cn2n−Cn+12n=Cn2nn+1 c ( n ) = C 2 n n − C 2 n n + 1 = C 2 n n n + 1

推论: n 个字符, 进栈出栈 (出栈可以在栈不为空的时候随时进行), 则出栈序列有 c(n) 种

这种先入后出的情形都是这样

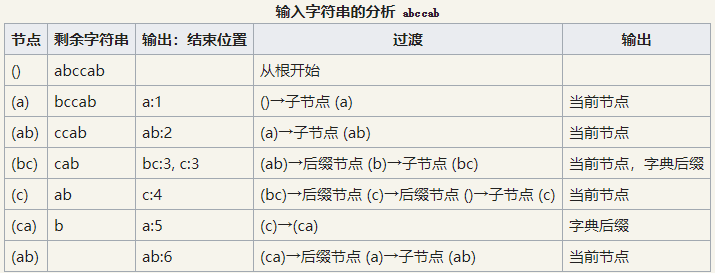
3. 基数树 (radixTree)

4. 字典树 (trie)

又叫前缀树(preifx tree). 适用于储存有公共前缀的字符串集合. 如果直接储存, 而很多字符串有公共前缀, 会浪费掉存储空间.
字典树可以看成是基数树的变形, 每个结点可以有多个孩子, 每个结点存储的是一个字符, 从根沿着结点走到一个结点, 走过的路径形成字符序列, 如果有合适的单词就可以输出.

当然, 也可以同理得出后缀树

4.1. AC 自动机

Aho-Corasick automation, 是在字典树上添加匹配失败边 (失配指针), 实现字符串搜索匹配的算法.

图中蓝色结点 表示存在字符串, 灰色表示不存在.
黑色边是父亲到子结点的边, 蓝色边就是失配指针.

蓝色边 (终点称为起点的后缀结点): 连接字符串终点到在图中存在的, 最长严格后缀的结点. 如 caa 的严格后缀为 aa,a, 空. 而在图中存在, 且最长的是字符串 a, 则连接到这个字符串的终点 a.

绿色边 (字典后缀结点): 终点是起点经过蓝色有向边到达的第一个蓝色结点.

下面摘自 wiki

在每一步中，算法先查找当前节点的 “孩子节点”，如果没有找到匹配，查找它的后缀节点 (suffix) 的孩子，如果仍然没有，接着查找后缀节点的后缀节点的孩子, 如此循环, 直到根结点，如果到达根节点仍没有找到匹配则结束。

当算法查找到一个节点，则输出所有结束在当前位置的字典项。输出步骤为首先找到该节点的字典后缀，然后用递归的方式一直执行到节点没有字典前缀为止。同时，如果该节点为一个字典节点，则输出该节点本身。

输入 abccab 后算法的执行步骤如下：

5. 平衡二叉树

上面的二叉查找树不平衡, 即经过多次插入, 删除后, 其高度变化大, 不能保持 Θ(n) Θ ( n ) 的性能
而平衡二叉树就能.
平衡二叉树都是经过一些旋转操作, 使左右子树的结点高度相差不大, 达到平衡
有如下几种

5.1. AVL Tree

平衡因子: 右子树高度 - 左子树高度
定义: 每个结点的平衡因子属于 {0,-1,1}

5.2. splayTree

伸展树, 它的特点是每次将访问的结点通过旋转旋转到根结点.
其实它并不平衡. 但是插入, 查找, 删除操作 的平摊时间是 O(logn) O ( l o g n )
有三种旋转, 下面都是将访问过的 x 旋转到 根部

5.2.1. Zig-step

5.2.2. Zig-zig step

5.2.3. Zig-zag step

5.3. read-black Tree

同样是平衡的二叉树, 以后单独写一篇关于红黑树的.

5.4. treap

前面提到, 随机构造的二叉查找树高度为 h=O(logn) h = O ( l o g n ) , 以及在算法 general 中说明了怎样 随机化 (shuffle) 一个给定的序列.

所以, 为了得到一个平衡的二叉排序树, 我们可以将给定的序列随机化, 然后再进行构造二叉排序树.

但是如果不能一次得到全部的数据, 也就是可能插入新的数据的时候, 该怎么办呢? 可以证明, 满足下面的条件构造的结构相当于同时得到全部数据, 也就是随机化的二叉查找树.

这种结构叫 treap, 不仅有要排序的关键字 key, 还有随机生成的, 各不相等的关键字priority, 代表插入的顺序.

• 二叉查找树的排序性质: 双亲结点的 key 大于左孩子, 小于右孩子
• 最小 (大) 堆的堆序性质: 双亲的 prority 小于 (大于) 孩子的 prority

插入的实现: 先进行二叉查找树的插入, 成为叶子结点, 再通过旋转 实现 上浮(堆中术语).
将先排序 key, 再排序 prority(排序 prority 时通过旋转保持 key 的排序)

6. 总结

还有很多有趣的树结构,
比如斜堆, 竞赛树 (赢者树, 输者树, 线段树, 索引树, B 树, fingerTree(不知道是不是译为手指树 233)…
这里就不详细介绍了, 如果以后有时间, 可能挑几个单独写一篇文章

7. 附代码

github 地址

7.1. 二叉树 (binaryTree)

from functools import total_ordering

@total_ordering
class node:
    def __init__(self,val,left=None,right=None,freq = 1):
        self.val=val
        self.left=left
        self.right=right
        self.freq = freq
    def __lt__(self,nd):
        return self.valdef __eq__(self,nd):
        return self.val==nd.val
    def __repr__(self):
        return 'node({})'.format(self.val)

class binaryTree:
    def __init__(self):
        self.root=None
    def add(self,val):
        def _add(nd,newNode):
            if ndif nd.right is None:nd.right = newNode
                else:_add(nd.right,newNode)
            elif nd>newNode:
                if nd.left is None:nd.left = newNode
                else : _add(nd.left,newNode)
            else:nd.freq +=1
        _add(self.root,node(val))
    def find(self,val):
        prt= self._findPrt(self.root,node(val),None)
        if prt.left and prt.left.val==val:
            return prt.left
        elif  prt.right and prt.right.val==val:return prt.right
        else :return None
    def _findPrt(self,nd,tgt,prt):
        if nd==tgt or nd is None:return prt
        elif ndreturn self._findPrt(nd.right,tgt,nd)
        else:return self._findPrt(nd.left,tgt,nd)
    def delete(self,val):
        prt= self._findPrt(self.root,node(val),None)
        if prt.left and prt.left.val==val:
            l=prt.left
            if l.left is None:prt.left = l.right
            elif l.right is None : prt.left = l.left
            else:
                nd = l.left
                while nd.right is not None:nd = nd.right
                nd.right = l.right
                prt.left = l.left
        elif  prt.right and prt.right.val==val:
            r=prt.right
            if r.right is None:prt.right = r.right
            elif r.right is None : prt.right = r.left
            else:
                nd = r.left
                while nd.right is not None:nd = nd.right
                nd.right = r.right
                prt.left = r.left

    def preOrder(self):
        def _p(nd):
            if nd is not None:
                print(nd)
                _p(nd.left)
                _p(nd.right)
        _p(self.root)

7.2. 前缀树 (Trie)

class node:
    def __init__(self,val = None):
        self.val = val
        self.isKey = False
        self.children = {}
    def __getitem__(self,i):
        return self.children[i]
    def __iter__(self):
        return iter(self.children.keys())
    def __setitem__(self,i,x):
        self.children[i] = x
    def __bool__(self):
        return self.children!={}
    def __str__(self):
        return 'val: '+str(self.val)+'\nchildren: '+' '.join(self.children.keys())
    def __repr__(self):
        return str(self)

class Trie(object):

    def __init__(self):
        self.root=node('')
        self.dic ={'insert':self.insert,'startsWith':self.startsWith,'search':self.search}

    def insert(self, word):
        """
        Inserts a word into the trie.
        :type word: str
        :rtype: void
        """
        if not word:return
        nd = self.root
        for i in word:
            if i in nd:
                nd = nd[i]
            else:
                newNode= node(i)
                nd[i] = newNode
                nd = newNode
        else:nd.isKey = True
    def search(self, word,matchAll='.'):
        """support matchall function  eg,  'p.d' matchs 'pad' , 'pid'
        """
        self.matchAll = '.'
        return self._search(self.root,word)
    def _search(self,nd,word):
        for idx,i in enumerate(word):
            if i==self.matchAll :
                for j in nd:
                    bl =self._search(nd[j],word[idx+1:])
                    if bl:return True
                else:return False
            if i  in nd:
                nd = nd[i]
            else:return False
        else:return nd.isKey
    def startsWith(self, prefix):
        """
        Returns if there is any word in the trie that starts with the given prefix.
        :type prefix: str
        :rtype: bool
        """
        nd = self.root
        for i in prefix:
            if i in  nd:
                nd= nd[i]
            else:return False
        return True
    def display(self):
        print('preOrderTraverse  data of the Trie')
        self.preOrder(self.root,'')
    def preOrder(self,root,s):
        s=s+root.val
        if  root.isKey:
            print(s)
        for i in root:
            self.preOrder(root[i],s)

7.3. 赢者树 (winnerTree)

class winnerTree:
    '''if i
    def __init__(self,players,reverse=False):
        self.n=len(players)
        self.tree = [0]*self.n
        players.insert(0,0)
        self.players=players
        self.reverse=reverse
        self.getNum()
        self.initTree(1)
    def getNum(self):
        i=1
        while 2*i< self.n:i=i*2
        if 2*i ==self. n:
            self.lowExt=0
            self.s = 2*i-1
        else:
            self.lowExt = (self.n-i)*2
            self.s = i-1
        self.offset = 2*i-1
    def treeToArray(self,p):
        return 2*p-self.offset if p>self.s else 2*p+self.lowExt-self.n+1
    def arrayToTree(self,i):
        return (i+self.offset)//2 if i<=self.lowExt else (i-self.lowExt+ self.n-1)//2
    def win(self,a,b):
        return aif self.reverse else a>b
    def initTree(self,p):
        if p>=self.n:
            delta = p%2  #!!! good job  notice delta mark the lchild or rchlid
            return self.players[self.treeToArray(p//2)+delta]
        l = self.initTree(2*p)
        r = self.initTree(2*p+1)
        self.tree[p] = l if self.win(l,r) else r
        return self.tree[p]
    def winner(self):
        idx = 1
        while 2*idx2*idx if self.tree[2*idx] == self.tree[idx] else idx*2+1
        num = self.treeToArray(idx)
        num = num+1 if self.players[num] !=self.tree[1] else num
        return self.tree[1],num
    def getOppo(self,i,x,p):
        oppo=None
        if 2*p2*p]
        elif i<=self.lowExt:oppo=self.players[i-1+i%2*2]
        else:
            lpl= self.players[2*p+self.lowExt-self.n+1]
            oppo = lpl if lpl!=x else self.players[2*p+self.lowExt-self.n+2]
        return oppo
    def update(self,i,x):
        ''' i is 1-indexed  which is the num of player
            and x is the new val of the player '''
        self.players[i]=x
        p = self.arrayToTree(i)
        oppo =self.getOppo(i,x,p)
        self.tree[p] = x if self.win(x,oppo) else oppo
        p=p//2
        while p:
            l = self.tree[p*2]
            r = None
            if 2*p+12+1]   #notice this !!!
            else:r = self.players[2*p+self.lowExt-self.n+1]
            self.tree[p] = l if self.win(l,r) else r
            p=p//2

7.4. 左斜堆

from functools import total_ordering
@total_ordering

class node:
    def __init__(self,val,freq=1,s=1,left=None,right=None):
        self.val=val
        self.freq=freq
        self.s=s
        if left is None or right is None:
            self.left = left if left is not None else right
            self.right =None
        else:
            if left.sdef __eq__(self,nd):
        return self.val==nd.val
    def __lt__(self,nd):
        return self.valdef __repr__(self):
        return 'node(val=%d,freq=%d,s=%d)'%(self.val,self.freq,self.s)

class leftHeap:
    def __init__(self,root=None):
        self.root=root
    def __bool__(self):
        return self.root is not None
    @staticmethod
    def _merge(root,t):  #-> int
        if root is None:return t
        if t is None:return root
        if rootif root.left is None or root.right is None:
            root.s=1
            if root.left is None:
                root.left,root.right = root.right,None
        else:
            if root.left.s1
        return root
    def insert(self,nd):
        if not isinstance(nd,node):nd = node(nd)
        if self.root is None:
            self.root=nd
            return
        if self.root==nd:
            self.root.freq+=1
            return
        prt =self. _findPrt(self.root,nd,None)
        if prt is None:
            self.root=leftHeap._merge(self.root,nd)
        else :
            if prt.left==nd:
                prt.left.freq+=1
            else:prt.right.freq+=1
    def remove(self,nd):
        if not isinstance(nd,node):nd = node(nd)
        if self.root==nd:
            self.root=leftHeap._merge(self.root.left,self.root.right)
        else:
            prt = self._findPrt(self.root,nd,None)
            if prt is not None:
                if prt.left==nd:
                    prt.left=leftHeap._merge(prt.left.left,prt.left.right)
                else:
                    prt.right=leftHeap._merge(prt.right.left,prt.right.right)
    def find(self,nd):
        if not isinstance(nd,node):nd = node(nd)
        prt = self._findPrt(self.root,nd,self.root)
        if prt is None or prt==nd:return prt
        elif prt.left==nd:return prt.left
        else:return prt.right
    def _findPrt(self,root,nd,parent):
        if not isinstance(nd,node):nd = node(nd)
        if root is None or rootreturn None
        if root==nd:return parent
        l=self._findPrt(root.left,nd,root)
        return  l if l is not None else self._findPrt(root.right,nd,root)
    def getTop(self):
        return self.root
    def pop(self):
        nd = self.root
        self.remove(self.root.val)
        return nd
    def levelTraverse(self):
        li = [(self.root,0)]
        cur=0
        while li:
            nd,lv = li.pop(0)
            if cur' ')
            else:print(nd,end=' ')
            if nd.left is not None:li.append((nd.left,lv+1))
            if nd.right is not None:li.append((nd.right,lv+1))