hihocoder 编程练习赛77

题目1 : 右转九十度

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

假设一个机器人在笛卡尔坐标系上。它从(X1, Y1)移动到了(X2, Y2)，然后向右转90度，继续前进。  

请你计算这个机器人继续前进过程中最先经过的整点是哪一个？

输入

四个整数X1, Y1, X2, Y2。

-1000000 ≤ X1, Y1, X2, Y2 ≤ 1000000 保证(X1, Y1)和(X2, Y2)是不同的点。

输出

两个整数X和Y代表最先经过的整点坐标。

样例输入

0 0 1 2

样例输出

3 1

 

题目分析:

1.题是什么?

    两个坐标,由坐标1运动到坐标2,然后右转90度继续运动,输出经过的第一个x与y皆为整数的点;

2.思路

    数学题自然数学解法求解

    我们设由到经过的第一个点为,令下面作图如下

现推理: 因为,,

              所以,所以

             所以

 我们要找第一个点,也就是最小的一组  和  , 与分别除以他们的最大公约数时自然就最小

             不知道怎么快速求两数字最大公约数的可以戳这儿(关于最大公约数求解算法的博客)

ac代码

#include 
#include 

int gcd(int a,int b){
	if(0==b) return a;
	return gcd(b,a%b);
}

void solve(){
	int x1,y1,x2,y2;
	scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
	int dy=y2-y1,dx=x1-x2,gcdxy=gcd(fabs(dx),fabs(dy));
	printf("%d %d\n",x2+dy/gcdxy,y2+dx/gcdxy);
}

int main(){
	solve();
	return 0;
}

题目2 : 钝角三角形

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

一个圆周上均匀分布着N个点，按顺时针编号依次是1, 2, 3, ... N。  

现在其中K个点是特殊点，编号分别是A1, A2, ... AK。  

小Hi想知道以特殊点为顶点，能构成多少个不同的钝角三角形。

输入

第一行包含2个整数N，K。  

第二行包含K个整数，A1, A2, ... AK。  

对于50%的数据，1 ≤ K ≤ MIN(1000, N)  

对于100%的数据，1 ≤ K ≤ MIN(100000, N), 1 ≤ N ≤ 1000000000, 1 ≤ Ai ≤ N

输出

一个整数代表答案

样例输入

8 4  
1 3 4 7

样例输出

1

 

题目分析:

1.题是什么?

     圆周上面有k个点,这k个都属于n个均匀分布于圆周的点,,现在问你我从这k个点中选3个连成一个三角形,是钝角三角形的可能数为多少?

2.思路

    问题的核心在于钝角三角形的判定.

    首先得了解一个初中定理,圆的直径对应的角为直角,也就是说如果我们对于题给的案例做分析:

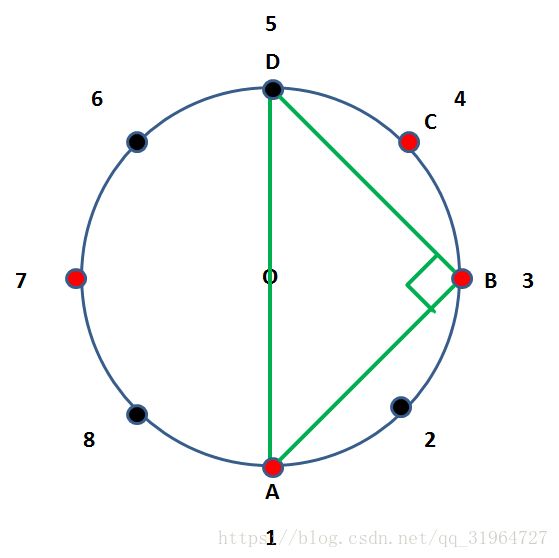
    如图,n=8,所以8个均分点,红色的代表是题目给的k个,如图1,3,4,7是红色,此时图中AD就是直径,因为是均分,这个自己看图理解一下,

    此时以ADB做三角形自然就是直接三角形(当然,D并不是k个中的一个,先理解),角ABD为直角.

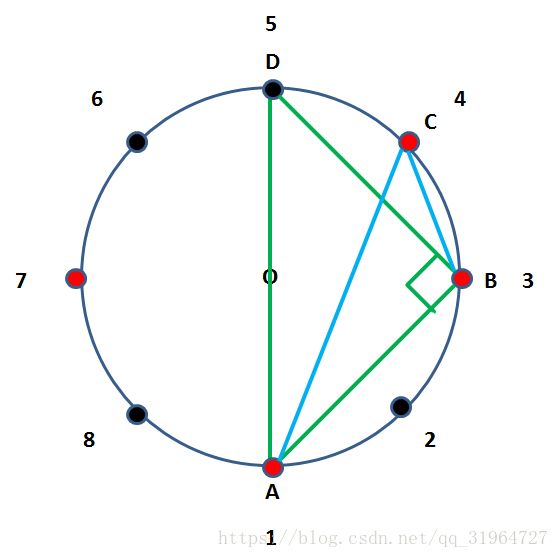
    那什么时候为钝角呢?自然是当所选的点比D更靠近B时,都是钝角,比如点C,因为在直角的基础上加上了角DBC.

    序号i为对面的点的序号是多少? 当然是(i+n/2)%n

    根据上面这通分析,我们其实就是要在这一堆原本表示序号的数字中找到对于每个点i,i和它对面的点之间的可用k点数目对2的组合数,这个答案就是以i点做钝角三角形,钝角偏右的可能总数.

ac代码

#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int maxn=100005;
int a[maxn];
ll cn2[maxn];

void initcn2(){
	for(ll i=2;i