ROAM: Recurrently Optimizing Tracking Model 阅读笔记

ROAM: Recurrently Optimizing Tracking Model

文章提出模型ROAM采用生成关于跟踪目标的heatmap响应和边框回归的方法跟踪目标：

1. 使用可调大小的卷积滤波器来适应对象的形状变化，模型无需设计锚点。
2. 采用离线训练递归神经优化器，元学习更新跟踪模型的方法，使模型能够迅速收敛。

Resizable Tracking Model

  模型包含两个部分：基础的跟踪模型和优化器。跟踪器包含两个分支：响应生成分支用于预测关于目标位置的heatmap和边框回归分支通过在滑动窗口上的框锚回归坐标偏移量来估计目标的精确框；两个分支共享backbone的feature map。离线学习的优化器使用元学习框架进行训练，在线更新跟踪模型。

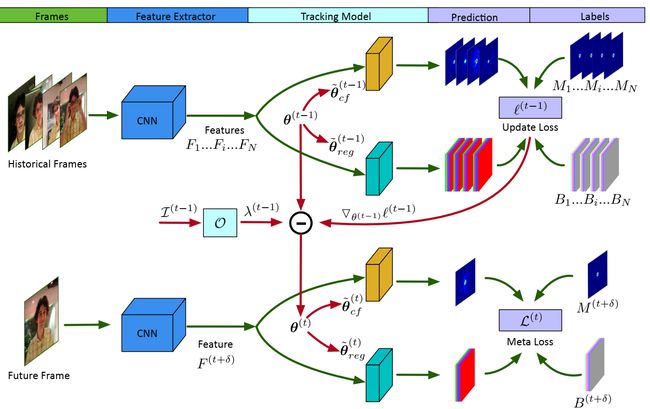
  给定一个训练批次patch（根据预测的目标边框剪切产生），通过backbone提取特征。根据当前目标尺寸将模型${\theta }^{\left(t-1\right)}$ warpe成 ${\theta }^{\left(t+1\right)}$，使用${\theta }^{\left(t+1\right)}$产生每个sample的响应图和边框。使用GT计算更新的损失$l\left(t-1\right)$及其梯度${\nabla }_{{\theta }^{\left(t-1\right)}}{l}^{\left(t-1\right)}$。
  包含以前学习率、当前参数、当前更新损失及其梯度的堆${\mathcal{I}}^{\left(t-1\right)}$输入到LSTM $\mathcal{O}$得到自适应自学习率${\lambda }^{\left(t-1\right)}$，模型进行单次梯度更新得到更新的模型${\theta }^{\left(t\right)}$，将更新后的模型${\theta }^{\left(t\right)}$应用于随机选择的未来帧，以获得最小化的元损失。
  针对目标形变可以考虑动态自适应的滤波器，但动态的滤波器意味着对于不同的图像目标需要有不同的参数量；为了解决这个问题，文章定义了fixed-shape convolutional filters，使用双线性插值根据目标尺寸改变滤波器尺寸。跟踪模型$\theta$包含两个部分：correlation filter ${\theta }_{cf}$和bounding box regression filter ${\theta }_{reg}$；两个都需要适应目标形状变化：
$$\theta =\left[{\theta }_{cf},{\theta }_{reg}\right]$$

$${\theta }_{cf}=\mathcal{W}\left({\theta }_{cf},\varphi \right)$$

$${\theta }_{reg}=\mathcal{W}\left({\theta }_{reg},\varphi \right)$$

$\mathcal{W}$利用双线性插值将滤波器resize成$\varphi =\left(f_r,f_c\right)$，滤波器尺寸根据以前的目标尺寸$\left(w,h\right)$计算：
$$f_r=\left[\frac{\rho h}{c}\right]-\lceil \frac{\rho h}{c}\rceil mod2+1$$

$$f_c=\left[\frac{\rho w}{c}\right]-\lceil \frac{\rho w}{c}\rceil mod2+1$$

$\rho$是尺度因子，使滤波器尺寸能够包含一定量的上下文信息，c是feature map的步长。由于可变尺寸的滤波器的存在，边框回归就不用考虑不同的宽高比和锚点框的尺寸问题了。只需要在每个空间位置设置一个固定尺寸的锚点框，与回归滤波器的尺寸对应：
$$\left(a_w,a_h\right)=\left(f_c,f_r\right)/\rho$$

每τ帧更新滤波器尺寸及锚点框，使用${\theta }^{\left(0\right)}$初始化跟踪器并在后续帧中进行连续优化。

Recurrent Model Optimization

响应生成器：$\mathcal{G}\left(F;{\theta }_{cf},\varphi \right)$，边框回归器：$\mathcal{R}\left(F;{\theta }_{reg},\varphi \right)$，θ是参数，F是输入的feature map，跟踪损失为
$$L\left(F,M,B;\theta ,\varphi \right)=|\mathcal{G}\left(F;{\theta }_{cf},\varphi \right)-M{|}^2+|\mathcal{R}\left(F;{\theta }_{reg},\varphi \right)-B{|}_s$$

第一项为L2，第二项为 Smooth L1，B为GT BBox，M是二维高斯响应，目标位置$\left(x_0,y_0\right)\left(w,h\right)$：

$$M\left(x,y\right)=e^{-\alpha \left(\frac{{\left(x-x_0\right)}^2}{{\sigma }_x^2}+\frac{{\left(y-y_0\right)}^2}{{\sigma }_y^2}\right)}$$

其中$\left({\sigma }_x,{\sigma }_y\right)=\left(w/c,h/c\right)$，$\alpha$用于控制响应图形状。在测试期间执行模型更新时，使用过去的预测作为伪标签，只在离线训练中使用GT。
跟踪网络的更新：
$${\theta }^{\left(t\right)}={\theta }^{\left(t-1\right)}-{\lambda }^{\left(t-1\right)}\odot {\nabla }_{{\theta }^{\left(t-1\right)}}{l}^{\left(t-1\right)}$$

学习率${\lambda }^{\left(t-1\right)}$由LSTM根据以前的学习率${\lambda }^{\left(t-2\right)}$、当前参数${\theta }^{\left(t-1\right)}$、更新损失${\ell }^{\left(t-1\right)}$
及其梯度${\nabla }_{{\theta }^{\left(t-1\right)}}{l}^{\left(t-1\right)}$得到：
$${\mathcal{I}}^{\left(t-1\right)}=\left[{\lambda }^{\left(t-2\right)},{\nabla }_{{\theta }^{\left(t-1\right)}}{l}^{\left(t-1\right)},{\theta }^{\left(t-1\right)},l^{\left(t-1\right)}\right]$$

$${\lambda }^{\left(t-1\right)}=\sigma \left(\mathcal{O}\left({\mathcal{I}}^{\left(t-1\right)};\omega \right)\right)$$

$\mathcal{O}\left(\cdot ;\omega \right)$是带参$\omega$的LSTM，σ是sigmoid。根据n个更新样本的小批量计算得到当前更新损失：
$$l^{\left(t-1\right)}=\frac{1}{n}\sum _{j=1}^{n}L\left(F_j,M_j,B_j;{\theta }^{\left(t-1\right)},{\varphi }^{\left(t-1\right)}\right)$$

样本$\left(F_j,M_j,B_j\right)$在过去的τ帧中选取。在随机选择的未来帧上测试新近更新的模型${\theta }^{\left(t\right)}$获得元损失：
$${\mathcal{L}}^{\left(t\right)}=L\left(F^{\left(t+\delta \right)},M^{\left(t+\delta \right)},B^{\left(t+\delta \right)};{\theta }^{\left(t\right)},{\varphi }^{\left(t-1\right)}\right)$$

δ 在[0，τ − 1]中随机产生。
在离线训练阶段对一小段视频执行上述过程，并获得平均元损失，以优化该优化器：
$$\overline{\mathcal{L}}=\frac{1}{NT}\sum _{i=1}^N\sum _{t=1}^T{\mathcal{L}}_{{\mathcal{V}}_i}^{\left(t\right)}$$

其中N是batch size，T是模型更新次数。${\mathcal{V}}_i\sim p\left(\mathcal{V}\right)$是从训练集采样的视频片段。初始模型参数${\theta }^{\left(0\right)}$和初始学习率${\lambda }^{\left(0\right)}$也是可训练参数，和优化器一同训练；通过最小化元损失就能够训练得到一个优化器。

Random Filter Scaling

  优化器由于过拟合的风险难以充分适应新任务，作者发现经过初步训练的优化器会预测相似的学习率。如果网络输入的变化幅度不够大，那么优化器容易过拟合。

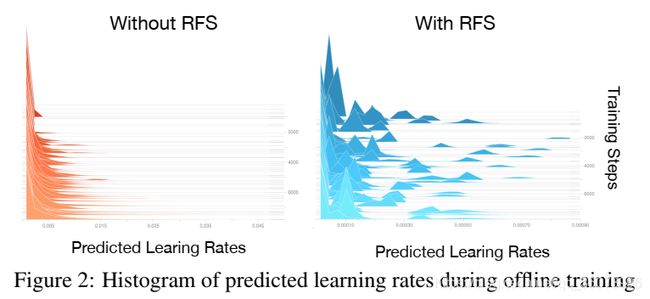
为了解决这个问题，将跟踪模型θ乘以随机采样的向量$ϵ$，该向量在离线训练的每次迭代中与θ的维数相同。
$$ϵ\sim \exp \left(\mathcal{U}\left(-\kappa ,\kappa \right)\right),{\theta }_{ϵ}=ϵ\odot \theta$$

$\mathcal{U}\left(-\kappa ,\kappa \right)$表示均匀分布，用$\kappa$控制尺度。目标函数修改为$g_{ϵ}\left(\theta \right)=g\left(\frac{\theta }{ϵ}\right)$，这在不修改训练样本（x; y）的情况下间接地缩放了网络输入x。

Online Tracking via Proposed Framework

跟踪的过程和离线训练相似，除了不用计算元损失及其梯度:
· Model Initialization
· Bounding Box Estimation
· Model Updating

Implementation Details

  Patch Cropping：$S=S_w=S_h=\gamma \sqrt{wh}$，γ是ROI的尺度因子，w、h是目标尺寸，裁剪出S×S的patch。
  Network Structure：VGG-16的前12层卷积并去掉最后的池化层。响应生成网络和边界框回归网络均由两个卷积层组成，其中第一层是512×64×1×1的降维层，第二层分别是64×1×21×21的correlation层或64×4×21×21的回归层；优化器O使用两个具有20个隐藏单元的堆叠LSTM层。
ROI比例因子为γ= 5，搜索区域S =281，滤波器大小的比例因子为ρ= 1：5；响应生成器α= 20，特征提取的feature map的步长c = 4。
  Training Details：ADAM…

Experiments

VOT&LaSOT:

GOT-10k:

…